Notes on "An Observation on Generalization"

原文链接： https://sumanthrh.com/post/notes-on-generalization/

Ilya Sutskever' Lecture: https://www.youtube.com/live/AKMuA_TVz3A

The talk is about really trying to understand why unsupervised learning works at all, and reason about it mathematically. To get there, Ilya first brings up the concept of learning itself (learning from data) and why machine learning works. The expectation here is that data has regularity, and machine learning models are expected to learn this regularity in our data. Bringing up the topic of supervised learning, he puts up this equation:

Low training error + more training data than “degrees of freedom” = Low test error

这次演讲的目的是真正尝试理解无监督学习为何有效，并从数学角度对其进行推理。为了达到这个目的，Ilya 首先提出了学习本身（从数据中学习）的概念以及机器学习为何有效。这里的期望是数据具有规律性，并且机器学习模型有望在我们的数据中学习这种规律性。在提出监督学习这个话题时，他提出了这个等式：

低训练误差 + 训练数据多于“自由度” = 低测试误差

Now, with unsupervised learning, the dream is that given all this unlabelled data (images, text chunks, etc) we expect a machine learning model to discover this “true”, hidden structure in the data. A key point with unsupervised learning is that we typically optimize a proxy objective (next work prediction or reconstruction) while we care about a different objective (learning hidden patterns in your data to do some sequence classification, perhaps). Why should this work?

现在，有了无监督学习，我们梦想着在给定所有这些未标记数据（图像、文本块等）的情况下，机器学习模型能够发现数据中这种“真实”的隐藏结构。无监督学习的一个关键点是，我们通常会优化代理目标（下一步工作预测或重建），而我们关心的是不同的目标（学习数据中的隐藏模式以进行一些序列分类）。为什么这样做有效？

Unsupervised learning via distribution matching

To get there, we first visit distribution matching. Consider two data sources $X$ and $Y$ which do not have any correspondence between each other. This could just look like datasets in different languages (say English and French) with no correspondence between samples. The idea with distribution matching is to find a mapping $F$ such that

为了实现这一点，我们首先讨论分布匹配。考虑两个数据源 $X$ 和 $Y$，它们之间没有任何对应关系。这可能看起来像不同语言（比如英语和法语）的数据集，样本之间没有对应关系。分布匹配的思想是找到一个映射 $F$，使得
$$
\begin{aligned}
distribution(F(X))\sim Y
\end{aligned}
$$
In our above example, this is: $distribution(F(English))\sim French$

There have been a number of methods proposed previously (A relevant example: unsupervised machine translation) that show that this can work even for high dimensional $X$ and $Y$.

之前已经提出了许多方法（相关示例：无监督机器翻译），这些方法表明即使对于高维 $X$ 和 $Y$ 也能发挥作用。

How can we reason about unsupervised learning now, with this background in mind?

考虑到这样的背景，我们现在该如何推理无监督学习呢？

Compression theory

Quoting Ilya here:

There is a one-to-one correspondence between all compressors and all predictors

所有压缩器和所有预测器之间存在一一对应关系

At first glance, this statement is not obvious at all! I think there can be an entire article on just this statement, but to really give an intuitive (and, unfortunately, qualitative) answer:

乍一看，这句话一点也不明显！我认为可以就这句话写一整篇文章，但要真正给出一个直观的（不幸的是，也是定性的）答案：

Consider the case of compressing a PNG file. The more predictable the pixel patterns in the image, the lesser the amount of truly unique information contained across pixels, the better you can compress it. Another example that I found helpful was from He’s talk on prediction and compression posted on LessWrong:

考虑压缩 PNG 文件的情况。图像中的像素模式越可预测，像素中包含的真正独特信息量就越少，压缩效果就越好。我发现另一个有用的示例来自关于预测和压缩的演讲 posted on LessWrong：

Let’s say you are trying to find an encoding for a string, where each character can only be “a”, “b”, “c” or “d”. Consider the string “abaaabaacbabaaabcd”. let’s take the simple encoding scheme below:

Char	Encoding
a	00
b	01
c	10
d	11

假设你正在尝试为一个字符串寻找一种编码，其中每个字符只能是“a”、“b”、“c”或“d”。考虑字符串“abaaabaacbabaaabcd”。让我们采用以下简单的编码方案：

Number of bits needed for the above string: 36 bits. Suppose that all the strings in our data have the following characteristics: “a"s appear the most frequent, while “c"s and “d"s apear rarely (this is roughly the case with our anecdotal example). Thus, you can use the modified encoding scheme below:

Char	Encoding
a	0
b	10
c	110
d	111

上述字符串所需的位数：36 位。假设我们的数据中的所有字符串都具有以下特征：“a”出现的频率最高，而“c”和“d”出现的频率则很低（我们的轶事示例大致如此）。因此，您可以使用以下修改后的编码方案：

Number of bits needed for the string: 29 bits. By being able to better predict the next character for each string, we’re able to better compress the string.

Now, with that in mind, let’s come back to the original discussion on unsupervised learning. In unsupervised learning, atleast in the realm of representation learning, we typically try to learn useful representations for our data, with the ultimate goal for using these learned representations for a downstream prediction task (say, training a linear classifier on top). A good unsupervised learning algorithm thus learns to perform good compression of your data. We will now use the language of compression (over prediction).

字符串所需的位数：29 位。通过能够更好地预测每个字符串的下一个字符，我们能够更好地压缩字符串。

现在，考虑到这一点，让我们回到最初关于无监督学习的讨论。在无监督学习中，至少在表示学习领域，我们通常尝试学习对我们数据的有用表示，最终目标是将这些学习到的表示用于下游预测任务（例如，在上面训练线性分类器）。因此，一个好的无监督学习算法会学会对数据进行良好的压缩。我们现在将使用压缩（过度预测）的语言。

A simple thought experiment

Consider two datasets $X$ and $Y$. Suppose we also have a good compression algorithm $C(data)$ - given a dataset $d$, the compressor $C$ will spit out a compressed object $C(d)$. Now, let’s say we concatenate $X$ and $Y$ and compress them jointly. A good compressor will now use the patterns in dataset $X$ to compress $Y$ :
$$
\begin{aligned}
\vert C(concat(X,Y))\vert\lt\vert C(X)\vert+\vert C(Y)\vert+O(1)
\end{aligned}
$$
(You can think of |⋅| to be some notion of size of the compressed object)

虑两个数据集 $X$ 和 $Y$。假设我们还有一个好的压缩算法 $C(data)$ - 给定一个数据集 $d$，压缩器 $C$ 将输出一个压缩对象 $C(d)$。现在，假设我们将 $X$ 和 $Y$ 连接起来并联合压缩它们。一个好的压缩器现在将使用数据集 $X$ 中的模式来压缩 $Y$：

The gap between the LHS and the RHS is dictated by the shared information/structure present in the two datasets, or the algorithmic mutual information.

LHS 和 RHS 之间的差距由两个数据集中存在的共享信息/结构或算法互信息决定。

Okay, but how does this relate back to unsupervised learning? $Y$ can be a dataset for a supervised task you care about (sequence classsification) while $X$ is data for your unsupervised task. Ilya also talks about how this generalizes distribution matching i.e if there exists a function $F$ such that $Distribution(F(X))∼=Distribution(Y)$, then a “good” compressor should be able to find and exploit this.Why? Well you can simply consider a 2D case where all datapoints in $X$ lie approximately on the line $y=x$ and all datapoints in $Y$ lie approximately on the line $y=2x$. Being able to find the transformation function $F$ will allow you to compress your combined dataset even further.

好的，但这与无监督学习有什么关系？$Y$ 可以是你关心的监督任务（序列分类）的数据集，而 $X$ 是你的无监督任务的数据。Ilya 还谈到了这如何概括分布匹配，即如果存在一个函数 $F$ 使得 $Distribution(F(X))∼=Distribution(Y)$，那么“好的”压缩器应该能够找到并利用这一点。为什么？好吧，你可以简单地考虑一个 2D 情况，其中 $X$ 中的所有数据点都大致位于直线 $y=x$ 上，而 $Y$ 中的所有数据点都大致位于直线 $y=2x$ 上。能够找到变换函数 $F$ 将使你能够进一步压缩组合数据集。

Formalization

Consider a machine learning algorithm $A$ that tries to compress $Y$. Suppose that the algorithm has access to dataset $X$. Now, we formalize our goal to be minimizing the regret of using this algorithm. The regret would be relative to a gold standard - in this case, in a qualitative sense, being able to get as much as we can from our unlabelled dataset $X$.

Low regret = “we got all the value” out of the unlabelled data, and nobody can do better!

考虑一个试图压缩 $Y$ 的机器学习算法 $A$。假设该算法可以访问数据集 $X$。现在，我们正式确定我们的目标，即尽量减少使用该算法的“遗憾”。“遗憾”将相对于黄金标准 - 在这种情况下，从定性意义上讲，能够从未标记的数据集 $X$ 中获取尽可能多的信息。

Kolmogorov complexity as the ultimate compressor

The Kolmogorov complexity of an object (this could be any data, really) is the length of the (or rather, a) shortest program that produces the object as its output. In essence, this is all the information you need to produce the output. If the program to create a 20MB image takes up 10 lines of code, then that program is a valid compression of your image. Taking this a step further, the following is true, for a (computable) compressor $C$:
$$
\begin{aligned}
K(X)\le\vert C(X)\vert+K(C)+O(1)
\end{aligned}
$$
一个对象（实际上可以是任何数据）的柯尔莫哥洛夫复杂度是产生该对象作为输出的最短程序（或者更确切地说是）的长度。本质上，这是产生输出所需的所有信息。如果创建 20MB 图像的程序占用 10 行代码，那么该程序就是对图像的有效压缩。更进一步，对于（可计算的）压缩器 $C$，以下是正确的：

While I won’t dive too much into this, you can reason about this better with the previous example of string compression. Let’s say we had no compressor i.e we’re simply storing the string in bits. Thus, if we had a $s$, and the length of the string $s$ in bits was $|s|$, then $K(s)≤|s|+O(1)$ (A simple relation from the definition of Kolmogorov complexity). Now, if we add in a compressor, the Kolmogorov complexity would be lesser than the size of the compressed object, along with the shortest description for the compressor.The proof for this can be summarized (rather brilliantly) in three words: The simulation argument. If you have an amazing compressor, then you should be able to simulate it using a computer program and, from the definition of Kolmogorov complexity, your new computer program, along with the size of the compressed object, can’t be shorter than the optimal, shortest program for simulating $X$ without doing any compression.

虽然我不会深入探讨这个问题，但您可以使用前面的字符串压缩示例更好地推理这一点。假设我们没有压缩器，即我们只是以位为单位存储字符串。因此，如果我们有一个 $s$，并且字符串 $s$ 的位长度为 $|s|$，则 $K(s)≤|s|+O(1)$（根据 Kolmogorov 复杂度的定义得出的简单关系）。现在，如果我们添加一个压缩器，Kolmogorov 复杂度将小于压缩对象的大小，以及压缩器的最短描述。对此的证明可以用三个词（相当精彩）总结：模拟论证。如果您有一个出色的压缩器，那么您应该能够使用计算机程序对其进行模拟，并且根据 Kolmogorov 复杂度的定义，您的新计算机程序以及压缩对象的大小不能短于模拟 $X$ 而不进行任何压缩的最佳、最短程序。

Right here, let’s pause, and let Ilya lay out a brilliant analogy to neural networks. Kolmogorov complexity is uncomputable for a general $X$ (I will let Wikipedia do all the heavy lifting for this one). Neural networks are computers, yes computers that can simulate different programs. SGD is the handy search algorithm that we use to efficiently search over the infinitely large space of programs/circuits.

就在这里，让我们暂停一下，让 Ilya 为神经网络做一个精彩的类比。对于一般的 $X$，Kolmogorov 复杂度是无法计算的（我将让 Wikipedia 来完成这一步的所有繁重工作）。神经网络是计算机，是的，可以 模拟 不同程序的 计算机。SGD 是一种方便的搜索算法，我们使用它来有效地搜索无限大的程序/电路空间。

Conditional Kolmogorov Complexity as the solution

We look at how conditional Kolmogorov complexity can be thought of as the solution we’re looking for in unsupervised learning. If $C$ is a computable compressor, then:

我们来看看条件柯尔莫哥洛夫复杂度如何被视为我们在无监督学习中寻找的解决方案。如果 $C$ 是可计算压缩器，那么：
$$
\begin{aligned}
\forall X, K(Y\vert X)\lt\vert C(Y\vert X)\vert+K(C)+O(1)
\end{aligned}
$$
First of all, what does the conditional Kolmogorov complexity mean? conditional Kolmogorov complexity here is the shortest program that can output $Y$, given that it can probe $X$ (or, use $X$ as an auxillary input). It quantifies how complex $Y$ is, given that you already know $X$. Consider this example: if $X$ is the collection of all the webpages on the internet, and $Y$ is just the information on www.google.com, then you can very easily describe a short program to get $Y$ given $X$, and thus $K(Y|X)$ is low. Similarly, if $X$ is just a dataset of random strings and Y is the information in www.google.com, then we don’t gain much from knowing about $X$, and $K(Y|X)$ is just $K(Y)$.

首先，条件柯尔莫哥洛夫复杂度是什么意思？这里的条件柯尔莫哥洛夫复杂度是指在可以探测 $X$（或者，使用 $X$ 作为辅助输入）的情况下，能够输出 $Y$ 的最短程序。它量化了在已知 $X$ 的情况下，$Y$ 的复杂度。考虑这个例子：如果 $X$ 是互联网上所有网页的集合，而 $Y$ 只是 www.google.com 上的信息，那么你可以很容易地描述一个简短的程序来在给定 $X$ 的情况下获得 $Y$，因此 $K(Y|X)$ 很低。同样，如果 $X$ 只是一个随机字符串的数据集，而 Y 是 www.google.com 中的信息，那么我们从了解 $X$ 中得不到太多好处，而 $K(Y|X)$ 只是 $K(Y)$。

Just compress everything

Some technicality on the conditional complexity mentioned above: instead of talking about “conditioning” on a dataset, where we’re talking about compressors that are compressing $Y$ while being able to “access” $X$, we can also view this with respect to the concatenated dataset $concat(X,Y)$. This is because in machine learning, we can fit over large datasets, but there’s no good way yet for “conditioning” on an entire dataset. A relation on the joint complexity of two datasets:

关于上面提到的条件复杂性的一些技术细节：我们不是谈论对数据集的“条件化”，我们谈论的是压缩器在压缩 $Y$ 的同时能够“访问” $X$，我们也可以从连接数据集 $concat(X,Y)$ 的角度来看待这一点。这是因为在机器学习中，我们可以适应大型数据集，但目前还没有很好的方法对整个数据集进行“条件化”。两个数据集的联合复杂性关系：
$$
\begin{aligned}
K(X,Y)=K(X)+K(Y\vert X)+O(log(K(X\vert Y)))
\end{aligned}
$$
This comes from the chain rule for Kolmogorov complexity. In words, this means that the shortest program that outputs $X$ and $Y$ can be obtained from the shortest program that outputs $X$, plus the shortest program that outputs $Y$ given $X$, plus some logarithmic factor. Or, as Ilya puts it

这来自 Kolmogorov 复杂度链式法则。换句话说，这意味着输出 $X$ 和 $Y$ 的最短程序可以通过输出 $X$ 的最短程序加上给定 $X$ 输出 $Y$ 的最短程序加上某个对数因子来获得。或者，正如 Ilya 所说

First, “generate” $X$, then “use” $X$ to generate $Y$, and this can’t be too different from generating the two datasets jointly

首先“生成”$X$，然后“使用”$X$生成$Y$，这与联合生成两个数据集没有太大区别

Thus, you can now simply talk about the old fashioned Kolmogorov compressor, that compressors two datasets $X$ and $Y$ jointly. Let’s come back to our main discussion: in unsupervised learning, we’re looking towards extracting as much value as we can out of some unlabelled data $X$, towards a goal of performing some kind of prediction on a test dataset that has the same distribution as some labelled data $Y$. We laid out how we can view unsupervised learning algorithms as being compressors, and using the equation above, you can see that the Kolmogorov complexity of the concatenated datasets is really the best you can do in terms of a good compressor, that extracts as much value as possible from $X$.

因此，现在您可以简单地讨论老式的 Kolmogorov 压缩器，它将两个数据集 $X$ 和 $Y$ 联合压缩。让我们回到我们的主要讨论：在无监督学习中，我们希望从一些未标记的数据 $X$ 中提取尽可能多的价值，目标是对具有与某些标记数据 $Y$ 相同分布的测试数据集执行某种预测。我们阐述了如何将无监督学习算法视为压缩器，使用上面的公式，您可以看到，连接数据集的 Kolmogorov 复杂度实际上是您能做到的最好的压缩器，它可以从 $X$ 中提取尽可能多的价值。

Joint compression is just Maximum Likelihood Estimation

Ilya now brings up an equivalence between joint compression and maximum likelihood. Suppose that we have a dataset $X = x_1,x_2,…x_N$. Then, the cost of “compressing” the dataset, using an unsupervised machine learning algorithm governed by parameters $θ$, is the negative log likelihood - the inability of your ML algorithm/compressor to correctly assign the highest possible probability for the data samples it has seen:

Ilya 现在提出了联合压缩和最大似然之间的等价关系。假设我们有一个数据集 $X = x_1,x_2,…x_N$。那么，使用由参数 $θ$ 控制的无监督机器学习算法“压缩”数据集的成本是负对数似然 - 您的 ML 算法/压缩器无法为其看到的数据样本正确分配最高可能概率：
$$
\begin{aligned}
Cost=-\sum_i^N log P(x_i\vert\theta)
\end{aligned}
$$
Adding another dataset - or performing joint compression, is simply adding more samples to the summation above.

A key takeway here: Neural networks/Transformers are computers performing joint compression of all your input data samples through maximum likelihood, and we use SGD to search over the infinitely large space of possible programs that perform compression, and choose a sufficiently good compressor.

添加另一个数据集（或执行联合压缩）只是在上面的总和中添加更多样本。

这里的关键点是：神经网络/Transformers 是通过最大似然对所有输入数据样本进行联合压缩的计算机，我们使用 SGD 在执行压缩的可能程序的无限大空间中进行搜索，并选择足够好的压缩器。

GPT

The GPT-N models trained by OpenAI can be understood by thinking about conditional distributions of text. During training, a causal language model like GPT is trained to perform next word prediction given a text chunk from some random document. By training over a huge, internet-scale corpus of such documents, these neural networks learn an internal model of different conditional distributions of text.

通过思考文本的条件分布，可以理解 OpenAI 训练的 GPT-N 模型。在训练过程中，像 GPT 这样的因果语言模型被训练为根据某个随机文档中的文本块来执行下一个单词预测。通过对此类文档的庞大互联网规模语料库进行训练，这些神经网络可以学习不同文本条件分布的内部模型。

Is this universal across data domains?

Can this work in the domain of computer vision, dealing with images or videos? Ilya brings up research from OpenAI to argue that this does work.

这可以在计算机视觉领域、处理图像或视频中发挥作用吗？Ilya 引用了 OpenAI 的研究来证明这确实有效。

iGPT

iGPT is an unsupervised transformer-based model trained on images. The data preprocessing is simple: They simply pre-process raw images by first resizing to a low resolution and then reshape into a 1D sequence. The model is trained to perform next-pixel prediction on these pixel sequences. Ilya now goes into more detail about the performance of iGPT across different scales, which I won’t talk about here. What is interesting, or important to note is that the performance of iGPT came pretty close to the best unsupervised models trained on ImageNet.

iGPT 是一个基于 Transformer 的无监督图像训练模型。数据预处理很简单：它们只是对原始图像进行预处理，首先将其调整为低分辨率，然后将其重塑为 1D 序列。该模型经过训练可对这些像素序列执行下一个像素预测。Ilya 现在将更详细地介绍 iGPT 在不同尺度上的表现，我在这里就不谈了。有趣的是，或者说值得注意的是，iGPT 的表现非常接近在 ImageNet 上训练的最佳无监督模型。

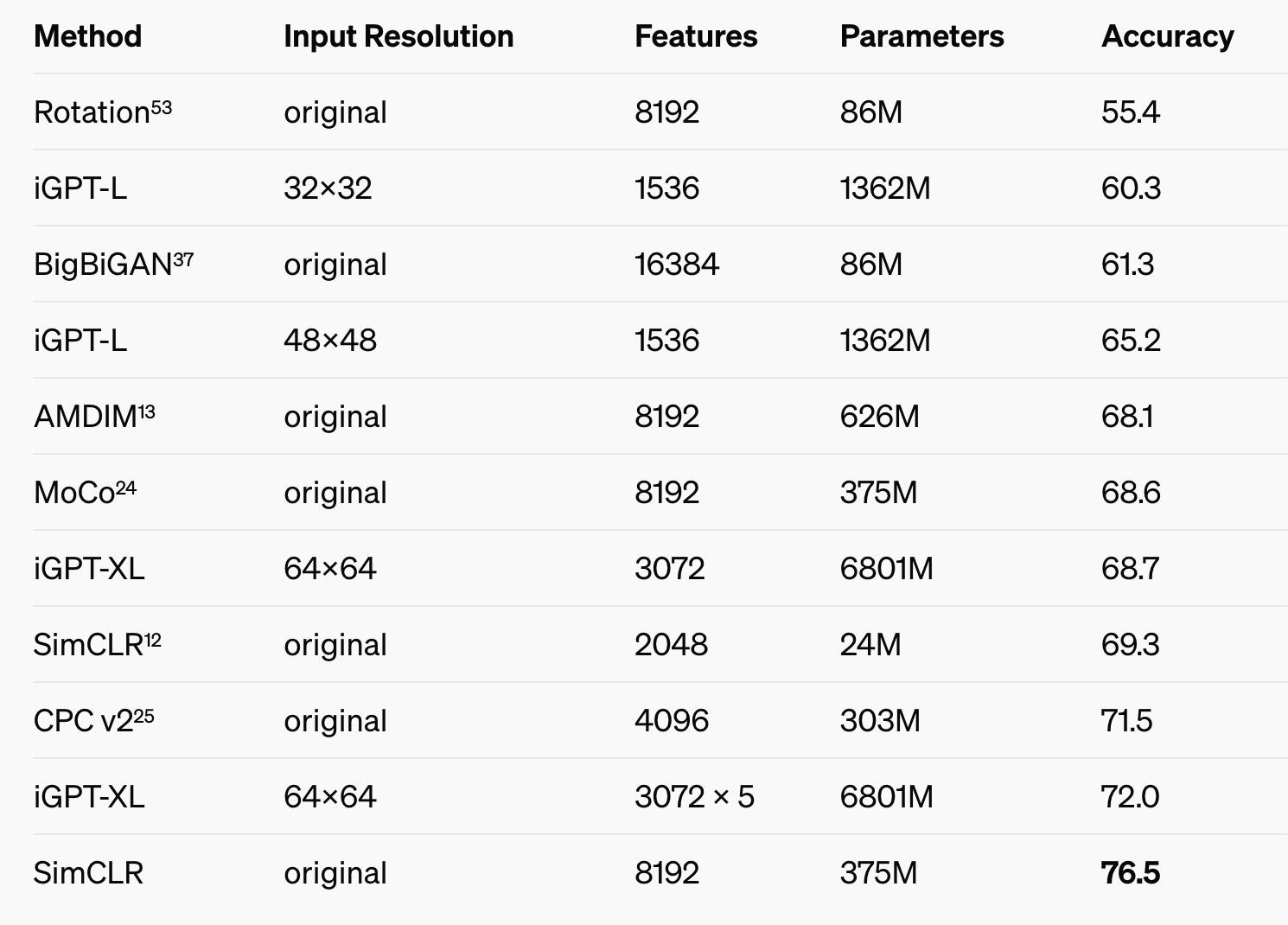
Linear probe accuracies compared across different models, taken from the iGPT paper. iGPT-XL, the largest iGPT model comes close to the performance of SimCLR, the best unsupervised learning method on ImageNet at the time. Note that SimCLR used full resolution images, while iGPT used the downscaled 64x64 images. Note also the difference in parameters - iGPT has 20x more parameters

不同模型的线性探测准确度比较，取自 iGPT 论文。最大的 iGPT 模型 iGPT-XL 接近当时 ImageNet 上最佳无监督学习方法 SimCLR 的性能。请注意，SimCLR 使用的是全分辨率图像，而 iGPT 使用的是缩小的 64x64 图像。还请注意参数的差异 - iGPT 的参数多 20 倍。

A comment on how linear probe accuracy is measured: iGPT and SimCLR provide a representation of the image - a good compression - and then a linear classifier is trained on top of this representation to perform classification. The accuracy of this linear classifier is the linear probe accuracy.

关于如何测量线性探测精度的评论：iGPT 和 SimCLR 提供了图像的表示 - 良好的压缩 - 然后在此表示的基础上训练线性分类器以执行分类。此线性分类器的精度就是线性探测精度。

Limitations/ Unanswered questions

These are some limitations or unanswered questions that are not addressed from the above compression theory on unsupervised learning. I don’t want to expand this section too much, so I will simply list out the points almost verbatim from Ilya’s talk:

• Compression theory does not immediately explain why representations are nice and linearly separable.
• Linear representations are so pervasive that the reason for their formation must be very fundamental, but this is not captured.
• Auto-regressive (AR) models seem to have better representations than BERT-like models. Ilya’s speculation here: With AR models, you need to predict the next word/ pixel based on all the previous word/ pixels, and you need to look at the entire context. This is not the case with BERT-like models, where you mask out a certain percentage of pixels/ words and then look a bit into the past and the future. The hardest prediction task in next word prediction is a lot harder than the hardest prediction task in masked language modeling.

这些是上述无监督学习压缩理论未解决的一些限制或未解答的问题。我不想过多地扩展此部分，因此我将简单地逐字逐句地列出 Ilya 演讲中的要点：

• 压缩理论并不能立即解释为什么表示是良好的并且是线性可分离的。
• 线性表示如此普遍，以至于它们形成的原因一定非常根本，但这并未被捕捉到。
• 自回归 (AR) 模型似乎比 BERT 类模型具有更好的表示。Ilya 的推测是：使用 AR 模型，您需要根据所有前一个单词/像素来预测下一个单词/像素，并且需要查看整个上下文。BERT 类模型并非如此，在 BERT 类模型中，您需要屏蔽一定比例的像素/单词，然后稍微回顾一下过去和未来。下一个单词预测中最难的预测任务比屏蔽语言建模中最难的预测任务要难得多。

Summary

• Ilya delves into the mathematical and conceptual foundations of unsupervised learning, formalizing how machine learning algorithms learn from unlabelled data by capturing its inherent regularities.
• Ilya 深入研究了无监督学习的数学和概念基础，形式化了机器学习算法如何通过捕捉未标记数据的固有规律来从中学习。
• Compression theory can be used to explain unsupervised learning. There is a one-to-one correspondence between all compressors and predictors, and a good unsupervised learning algorithm needs to perform good compression of your data, to get good prediction on a downstream supervised learning task.
• 压缩理论可用于解释无监督学习。所有压缩器和预测器之间都存在一一对应关系，良好的无监督学习算法需要对数据进行良好的压缩，才能在下游监督学习任务中获得良好的“预测”。
• Kolmogorov complexity can be viewed as the gold standard for compression. In unsupervised learning, we’re looking towards extracting as much value as we can out of some unlabelled data X, towards a goal of performing some kind of prediction on a test dataset that has the same distribution as some labelled data Y. Unsupervised learning algorithms are trained to be good joint compressors via maximum likelihood, and the Kolmogorov complexity of the concatenated datasets is the best you can do in terms of a good compressor, that extracts as much value as possible from X.
• 柯尔莫哥洛夫复杂度可以被视为压缩的黄金标准。在无监督学习中，我们希望从一些未标记的数据 X 中提取尽可能多的价值，目标是对具有与某些标记数据 Y 相同分布的测试数据集执行某种预测。无监督学习算法通过最大似然法训练为良好的联合压缩器，而连接数据集的柯尔莫哥洛夫复杂度是您在良好的压缩器方面可以做到的最佳值，它可以从 X 中提取尽可能多的价值。
• Neural networks are computers that can simulate different programs, and SGD is the handy search algorithm that we use to efficiently search over the infinitely large space of programs/circuits to get as close as we can to the optimal program (Kolmogorov complexity).
• 神经网络是可以模拟不同程序的计算机，而 SGD 是一种方便的搜索算法，我们使用它来有效地搜索无限大的程序/电路空间，以尽可能接近最佳程序（Kolmogorov 复杂度）。
• The Generalized Pre-trained Transformers (GPT) models by OpenAI and their variants in other domains like computer vision (iGPT) are some real-world examples of unsupervised learning via the proxy task of next-token/pixel prediction. Next-token/pixel prediction has been shown to be a good proxy to learn the true, hidden structure in your data i.e to perform good compression.
• OpenAI 的通用预训练 Transformers (GPT) 模型及其在计算机视觉 (iGPT) 等其他领域的变体是通过下一个标记/像素预测的代理任务进行无监督学习的一些真实示例。事实证明，下一个标记/像素预测是学习数据中真实隐藏结构（即执行良好压缩）的良好代理。
• Some limitations of this theory are that it does not explain the linear representations we obtain from good unsupervised learning algorithms, and we also don’t understand why auto-regressive modelling is superior to masked language modelling in learning good representations.
• 该理论的一些局限性在于，它不能解释我们从良好的无监督学习算法中获得的线性表示，我们也不明白为什么自回归建模在学习良好的表示方面优于掩蔽语言建模。