CMC：对比多视角编码

动物通过多个渠道感知世界，例如：眼睛接受光波较长的光渠道和耳朵接受高频的振动驱动。每个渠道都是有噪音的和不完备的，但是所有视角共享相同的重要因素，例如：物理、几何、以及语义。CMC作者提出了一个假设：一个表达力较强的表示应能够建模多视角不变的因素。因此，作者们在多视角对比学习框架下研究该假设，主要方式是最大化相同场景不同视角之间的互信息，反之最小化。最终，该方法可以扩展到任何数量的视角。如图1所示，CMC框架。

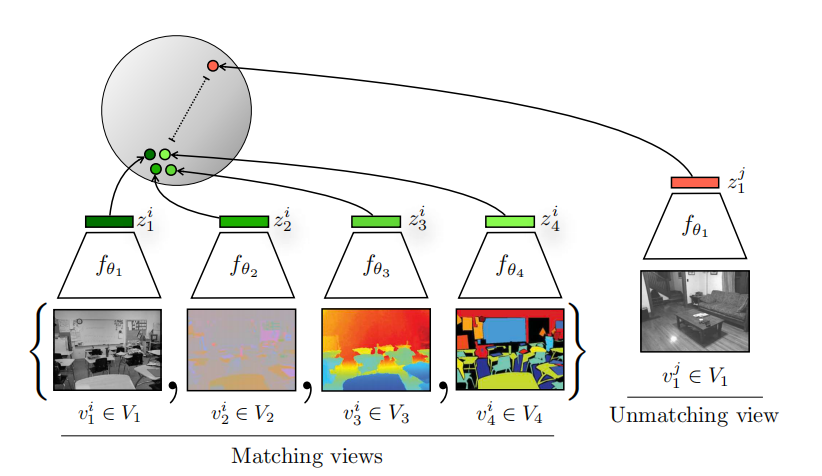
图1 CMC框架概览

对于每个视角来说，共享的重要因素是好的信息，而其它信息均为噪音，例如：这里有一条狗是个好信息，因为它可被看到、听到、以及感知到，而相机位姿是坏信息。在这个框架下，对应一个归纳偏差是：观看场景的方式应该不影响它的语义。该归纳偏差在认知科学是得到证明的。因此，CMC作者们利用相同场景的多个视角自然数据中共现作为监督信号。对于视觉，可利用的渠道有亮度、色度、深度、以及光流。

算法设计

CMC的学习目标是学习可以捕获多传感器视角之的共享信息的表示。在CMC中考虑数据的$M$个视角，被称为$V_1,\ldots,V_{M}$。对于每个视角$V_{i}$，随机变量$v_i$服从分布$\mathcal{P}(V_i)$。

两个视角的对比学习

给定数据集$V_1$和$V_2$由样本集$\{v_1^i,v_2^i\}_{i=1}^N$构成。若样本来自联合分布$x\sim p(v_1,v_2)$或$x=\{v_1^{i},v_2^{i}\}$，实质就是来自同一分布不同视角的样本$v_1,v_2$，那么该样本被称为正样本。若样本来自边缘分布$y\sim p(v_1)p(v_2)$或$y=\{v_1^i,v_2^j\}$，实则是来自不同分布不同视角的样本$v_1,v_2$，则被称为负样本。

CMC学习一个“评论者“函数$h_{\theta}(\cdot)$，对正样本输出较高的值，对负样本输出较低的值。与CPC相似，训练”评论者“函数从而能够从集合$S=\{x,y_1,y_2,\ldots,y_k\}$中选择出正样本$x$，目标函数为
$$
\begin{aligned}
\mathcal{L}_{contrast}=-\underset{S}{\mathbb{E}}[log\frac{h_{\theta}(x)}{h_{\theta}(x)+\sum_{i=1}^k h_{\theta}(y_i)}]
\end{aligned}\tag{1}
$$
简单来说，固定一个视角，从其它视角穷举正样本和负样本，那么目标函数为
$$
\begin{aligned}
\mathcal{L}_{contrast}^{V_1,V_2}=-\underset{\{v_1^1,v_2^1,\ldots,v_2^{k+1}\}}{\mathbb{E}}[log\frac{h_{\theta}(\{v_1^1,v_2^1\})}{\sum_{i=1}^{k+1} h_{\theta}(\{v_1^1,v_2^j\})}]
\end{aligned}\tag{2}
$$
在CPC中，式(2)被称为InfoNCE。

评论者的实现

为了抽取$v_1$和$v_2$的隐藏层表示$z_1,z_2$，那么利用两个编码器网络$f_{\theta_1}(\cdot)$和$f_{\theta_2}(\cdot)$。若以两个隐藏层表示$z_1,z_2$之间的余弦相似度作为分数，那么评论者可表示为
$$
\begin{aligned}
h_{\theta}(\{v_1,v_2\})=exp(\frac{f_{\theta_1}(v_1)\cdot f_{\theta_2}(v_2)}{\Vert f_{\theta_1}(v_1)\Vert\cdot\Vert f_{\theta_2}(v_2)\Vert})\cdot\frac{1}{\tau}
\end{aligned}\tag{3}
$$
为了对称，不仅以$V_1$为锚穷举$V_2$，还以$V_2$为锚穷举$V_1$，即
$$
\begin{aligned}
\mathcal{L}(V_1,V_2)=\mathcal{L}_{contrast}^{V_1,V_2}+\mathcal{L}_{contrast}^{V_2,V_1}
\end{aligned}\tag{4}
$$

与互信息的关系

CMC作者们通过推导证明了，最优评论者$h^{*}_{\theta}$与联合分布$p(z_1,z_2)$和边缘分布乘积$p(z_1)p(z_2)$之比成比例，即
$$
\begin{aligned}
h^{*}_{\theta}(\{v_1,v_2\})\propto\frac{p(z_1,z_2)}{p(z_1)p(z_2)}\propto\frac{p(z_1\vert z_2)}{p(z_1)}
\end{aligned}\tag{5}
$$
式(5)的量是样本对的互信息，在CPC中得到了证明，那么表明
$$
\begin{aligned}
I(z_i;z_j)\ge log(k)-\mathcal{L}_{contrast}
\end{aligned}\tag{6}
$$
式(6)中$k$为负样本数量。

因此，最小化损失函数$\mathcal{L}_{contrast}$，就是最大化编码$z_i,z_j$之间的互信息的下界。根据数据处理不等式，编码互信息的上界为$I(v_i;v_j)$。根据式(6)，可知，$k$越大，负样本量越大，那么编码$z_i,z_j$之间的互信息越大，$v_i,v_j$之间的互信息也越大，即正样本对$v_i,v_j$之间的互信息也越大。

多个视角的对比学习

如图2所示，作者们呈现了式(2)的通用表示，分别为“核心视角”和“全图”，这种表示方式提供了效率与有效性之间的平衡。

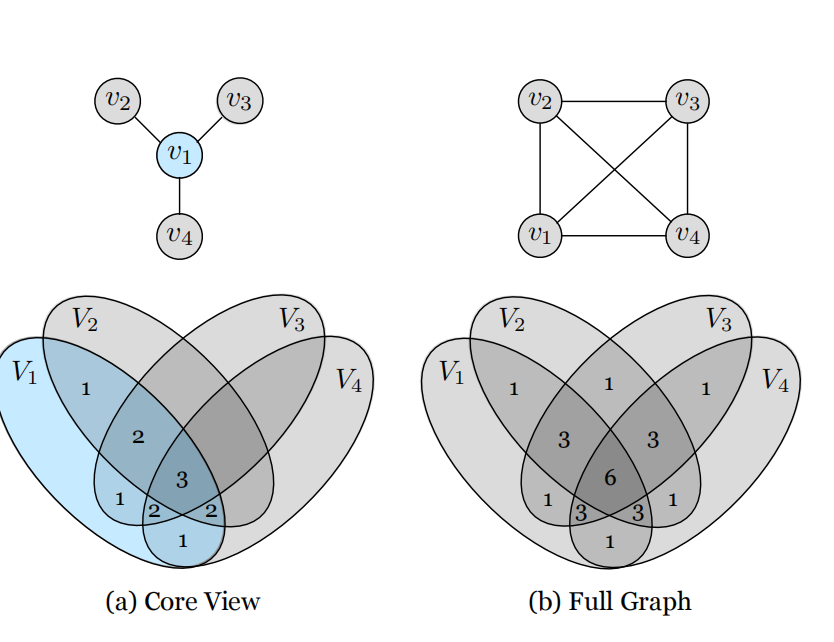
图2 图模型与信息图

对于核心视角，其表达式为
$$
\begin{aligned}
\mathcal{L}_{C}=\sum_{j=2}^M\mathcal{L}(V_1,V_2)
\end{aligned}\tag{7}
$$
对于全图，其表达式为
$$
\begin{aligned}
\mathcal{L}_{F}=\sum_{1\le i\lt j\le M}\mathcal{L}(V_i,V_j)
\end{aligned}\tag{8}
$$
以上两个方程均表现出：信息的贡献程度与共享该信息的视角数量成比例。如图2中信息图所示，信息的不同部分呈现不同的贡献度，数值越大代表信息的贡献度越大，共享该信息的视角也越多，即式(7),(8)展现的效果与信息图一致。其中，全图的计算量与视角的组合数有关，呈几何复杂度，但是能够捕获更多信息。

对比损失的实现

极端情况下，在式(2)的分母中包含所有数据样本，那么就需要计算全softmax损失，从而产生很高的计算复杂度。一种近似的方式是NCE(Noise-Contrastive Estimation)。另一种方式是随机采样$m$个负样本。同时，为了减少特征重复计算，还利用memory bank存储特征。同时，作者们指出这里的NCE不是暗指InfoNCE，而是InfoNCE的近似。

相关思考

SimCLR是基于数据增强的方式学习表示，而CMC是多视角共享信息的方式学习表示。SimCLR相对简单，但是CMC能够学习的表示泛化性更强。在损失函数方面，CMC的分母包含正样本对，而SimCLR与之不同。