基于非参数实例判别的无监督特征学习

在监督学习任务中，发现，深度神经网络能够捕获语义相似性。如图1所示，在图片分类任务中，豹的子类与豹这个类别的可能性是最高的，而其它与豹完全不相关的类别的可能性最低，这说明深度神经网络能够捕获类别语义的相似性。这种语义相似性不是语义标签带来的，而是直接从视觉数据中学习得到的。那么，进一步地，能否学习一种表示，它能够反映出实例之间的相似性。

图1 监督学习任务中模型效果

UFL作者们以无监督学习进行实例判别的方式，学习出这种表示。在实例判别中，由于类别的数量是整个训练集的大小，这对于分类模型是很困难的。为了处理该挑战，作者们基于NCE(noise-contrastive estimation)近似full softmax分布，利用近似正则化方法稳定化学习过程。在模型评估时，选择KNN算法评估学习出的表示，而不是线性分类器。这是因为使用线性分类器的前提假设是学习出来的表示具有线性可分性，这是没有得到证明的。最终，学习出的表示在ImageNet 1K分类任务中实现46.5%的Top-1准确率，在Places 205数据集中实现41.5%的准确率。

算法设计

如图2所示，UFL是一个实例级别的无监督特征学习方式，每张图片为一个类别。

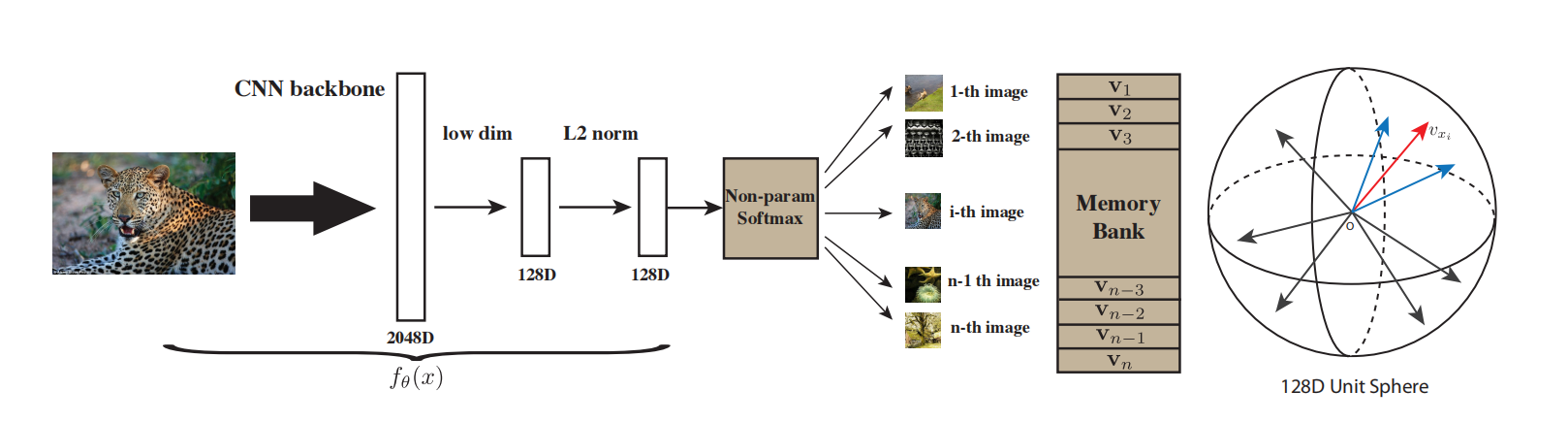
图2 无监督特征学习方式的pipeline

在模型训练阶段，维护一个memory bank $V$用于存储上个时间步的每个实例的表示。每次迭代，从$V$中获取数据$x_i$的表示$\mathbf{v}_i$，深度神经网络基于输入$x_i$输出表示$v$，再利用式(1)计算样本$x_i$属于$i$的概率$P(i\vert f_{\theta}(x_i))$。
$$
\begin{aligned}
P(i\vert v)=\frac{exp(\mathbf{v}_i^T\mathbf{v})/\tau}{\sum_{j=1}^nexp(\mathbf{v}_j^T\mathbf{v}/\tau)}
\end{aligned}\tag{1}
$$
其中，式(1)中参数$\tau$控制着表示分布的集中程度。可以理解为：控制着表示在图2单位球中分布的集中程度。
$$
\begin{aligned}
J(\theta)=-\sum_{i=1}^nlogP(i\vert f_{\theta}(x_i))
\end{aligned}\tag{2}
$$

每次模型迭代以式(2)为损失函数基于随机梯度下降更新参数$\theta$，再用之前计算的$f_i$更新表示$f_i\to\mathbf{v_i}$。

NCE

在减少式(1)中softmax的计算量方面，常用的技术有Hierarchical Softmax、NCE、以及负采样。在UFL中，作者们利用NCE作为优化方法。

NCE的基本思想是把多类别分类问题变为二分类问题。其中，二分类问题被定义为区分数据样本和噪音样本。确切的说，就是判断该样本是来自数据的分布，还是噪音分布。

若表示$\mathbf{v}$对应于样本$i$的概率为
$$
\begin{aligned}
P(i\vert\mathbf{v})=\frac{exp(\mathbf{v}^T\mathbf{f}_i/\tau)}{Z_i}
\end{aligned}\tag{3}
$$
其中，标准化常量$Z_i=\sum_{i=1}^nexp(\mathbf{v}_j^T\mathbf{f}_i/\tau)$

若噪音分布为均匀分布：$P_{n}=\frac{1}{n}$，噪音样本的频次是数据样本的$m$倍，那么样本$i$和表示$\mathbf{v}$为数据分布的概率为
$$
\begin{aligned}
h(i,\mathbf{v}):=P(D=1\vert i,\mathbf{v})=\frac{P(i\vert\mathbf{v})}{P(i\vert\mathbf{v})+mP_{n}(i)}
\end{aligned}\tag{4}
$$
最终，二分类问题的损失函数为
$$
\begin{aligned}
J_{NCE}(\theta)=-E_{P_d}[logh(i,\mathbf{v})]-m\cdot E_{P_n}[log(1-h(i,\mathbf{v}'))]
\end{aligned}\tag{5}
$$
式(5)中$\mathbf{v}'$为另一个图片在memory bank中的表示。

为了降低标准化常量$Z_i$的计算量，利用Monte-Carlo采样作为近似估计器
$$
\begin{aligned}
Z\simeq Z_i\simeq nE_j[exp(\mathbf{v}_j^T\mathbf{f}_i)/\tau]=\frac{n}{m}\sum_{k=1}^{m}exp(\mathbf{v}_{jk}^T\mathbf{f}_i/\tau)
\end{aligned}\tag{6}
$$
式(6)中$\{j_k\}$为随机子集的索引。

相关思考

在解决softmax计算复杂度的问题上，Hierarchical Softmax是构建哈夫曼树的方式减少计算量；负采样直接采样少量负样本的方式降低计算量；NCE是把多分类问题变为二分类问题。负采样的方法简单粗暴，精度低；Hierarchical Softmax精度高，但也很复杂；NCE应该是两者的折中，即保证了一定精度，也保证了一定的计算效率。