IMPALA：分布式RL框架

为了使单一参数的单个智能体能够解决大量任务，IMPALA作者们提出了重要性权重Actor-Learner架构，可见图1所示。若要智能体同时掌握各种各样的技能，面对最大的挑战是可扩展性，例如：A3C智能体掌握一个领域就需要数十亿的数据和很长时间的训练，更不敢想象一次掌握数十个领域了。

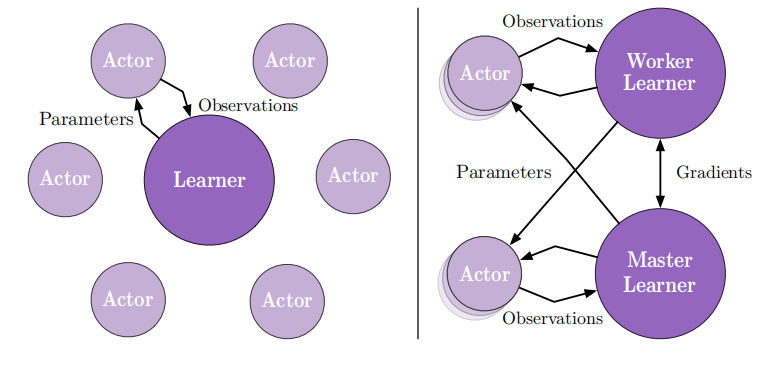
IMPALA可以在不牺牲训练稳定性或数据效率的情况下，扩展到数千台机器。A3C算法的训练方式是交互策略模型与共享模型交流梯度信息，而IMPALA架构中workers与中心的learners交流轨迹经验。由于worker中的策略可能落后于learner的策略，因此该学习为off-policy。同时，作者们也引入了V-trace，用于纠正这种有害的差异。基于扩展式架构与V-trace，IMPALA可实现高的数据吞吐量，且对超参数值和网络架构鲁棒性更强。

在IMPALA框架提出之前，主要是基于DistBelief的分布式异步SGD更新网络参数方法的扩展。其中，分布式DQN、进化策略、BA3C、以及Ape-X均是基于在分布式异步SGD更新网络参数，从而并行化深度强化学习。

IMPALA

如图1所示，IMPALA基于actor-critic架构学习策略$\pi$和价值函数$V^\pi$，生成经验的过程和学习$\pi$、$V^\pi$的过程属于解耦合的关系。该架构由生成经验轨迹的actor集合与利用经验学习策略的learner集合构成。与A3C不同， IMPALA中actors生成轨迹，再把轨迹发送给learner，而不是发送梯度，因此通信量大大的降低。对于参数更新，IMPALA利用的是分布式同步参数更新，这对扩展到多台机器时数据效率很重要。

V-trace

V-trace算法是一种off-policy算法。这类算法的目标是利用行为策略$\mu$生成的轨迹，学习策略$\pi$的价值函数$V^{\pi}$，被称为目标策略(target policy)。

V-trace target

考虑actor在策略$\pi$下生成的轨迹$(x_T,a_t,r_t)_{t=s}^{t=s+n}$，那么状态$x_s$下的n-steps V-trace的目标$V(x_s)$被定义为
$$
\begin{aligned}
v_s\overset{def}{=}V(x_s)+\sum_{t=s}^{s+n-1}\gamma^{t-s}(\prod_{i=s}^{t-1}c_i)\delta_tV
\end{aligned}\tag{1}
$$
式(1)中$\delta_tV\overset{def}{=}\rho_t(r_t+\gamma V(x_{t+1})-V(x_t))$是价值函数的时序差分，$\rho_t\overset{def}{=}min(\bar{\rho},\frac{\pi(a_t\vert x_t)}{\mu(a_t\vert x_t)})$与$c_i\overset{def}{=}min(\bar{c},\frac{\pi(a_i\vert x_i)}{\mu(a_i\vert x_i)})$是被裁剪的重要性采样权重。若$s=t$，那么$\prod_{i=s}^{t-1}c_i=1$。$\bar{\rho}$与$\bar{c}$之间的关系为$\bar{\rho}\ge\bar{c}$。

在on-policy的情况下，假设$\bar{c}\ge1$，那么所有的$c_i=1,p_t=1$，式(1)变为
$$
\begin{aligned}
v_s &= V(x_s)+\sum_{t=s}^{s+n-1}\gamma^{t-s}(r_t+\gamma V(x_{t+1}-V(x_t))) \\
&= \sum_{t=s}^{s+n-1}\gamma^{t-s}r^t+\gamma^nV(x_{s+n})
\end{aligned}\tag{2}
$$
即变为on-policy n-steps Bellman目标。

值得注意的是，权重$c_i$与$p_t$扮演不同的角色。权重$\rho_t$出现在时序差分$\delta_tV$的定义中，定义了更新规则的固定点，也可称收敛点。在表格场景中，模型更新的固定点是策略$\pi_{\bar{\rho}}$下价值函数$V^{\pi_{\bar{\rho}}}$。其中，策略被定义为
$$
\begin{aligned}
\pi_{\bar{\rho}}(a\vert x)\overset{def}{=}\frac{min(\bar{\rho}\mu(a\vert s),\pi(a\vert x))}{\sum_{b\in A}min(\bar{\rho}\mu(b\vert x),\pi(b\vert x))}
\end{aligned}\tag{3}
$$
根据式(3)，可知，若$\bar{\rho}\to+\infty$，那么价值函数$V^{\pi}$就是目标策略；若$\bar{\rho}\lt+\infty$，那么价值函数$V^{\pi_{\bar{\rho}}}$就是固定点，其中策略$\pi_{\bar{\rho}}$在策略$\mu$与$\pi$之间；若$\bar{\rho}\to 0$，那么可得到行为策略的价值函数$V^{\mu}$。

权重$c_i$类似于Retrace算法的"trace cutting"，它们的乘积表示时刻$t$的时序差分$\delta_tV$对时刻$s$价值函数的影响。若$\pi$与$\mu$的相似度越低，乘积的方差也就越大。因此$\bar{c}$为方差缩减技术。这种裁剪并不会影响拟合的解决方法。

总的来说，$\bar{c}$影响的式拟合速度，而$\bar{\rho}$影响的是拟合的价值函数。

Actor-critic algorithm

为了简单描述，这里给出三个公式，以表达V-trace Actor-Critic算法。

在时刻$s$下价值函数目标为$v_s$，价值函数参数$\theta$的梯度更新方向为
$$
\begin{aligned}
(v_s-V_{\theta}(x_s))\nabla_{\theta}V_{\theta}(x_s)
\end{aligned}\tag{4}
$$
策略参数$w$的更新方向为
$$
\begin{aligned}
\rho_{s}\nabla_wlog\pi_{w}(a_s\vert x_s)(r_s+\gamma v_{s+1}-V_{\theta}(x_s))
\end{aligned}\tag{5}
$$
为了阻止过早的拟合，可增加熵
$$
\begin{aligned}
-\nabla_w\sum_a\pi_{w}(a\vert x_s)log\pi_{w}(a\vert x_s)
\end{aligned}\tag{6}
$$
网络整体是(4),(5),(6)三个梯度以合适的系数求和而更新。

总的来说，IMPALA框架是以同步参数更新作为更新方式的可扩展多机的V-trace actor-critic算法框架。