RoFormer：旋转位置编码增强Transformer

经典Transformer架构的位置编码属于绝对位置编码，即没有显式的包含相对位置信息。RoPE作者提出了旋转位置编码，利用旋转矩阵编码位置信息，且显式的包含相对位置信息。同时，对RoPE的推导和理论解释给出了详细的表述。

问题定义

为了包含相对位置信息，作者们定义了查询向量$\mathbf{q}_m$与键向量$\mathbf{k}_{n}$的内积函数$g$，可见式(1)
$$
\begin{aligned}
\langle\mathbf{q}_m,\mathbf{k}_n\rangle=\langle f_q(x_m,m),f_{k}(x_n,n)\rangle=g(x_m,x_n,m-n)
\end{aligned}\tag{1}
$$
因此，其目标是寻找一个编码方式，从而使式(1)成立

旋转位置编码

2D

作者们先讨论了2维的情况，利用了2D平面的几何特性和复数形式，其函数为
$$
\begin{aligned}
f_q(x_m,m)&=(\mathbf{W}_qx_m)e^{im\theta} \\
f_{k}(x_n,n)&=(\mathbf{W}_kx_n)e^{in\theta} \\
g(x_m,x_n,m-n)&=Re[(\mathbf{W}_qx_m)(\mathbf{W}_kx_n)^{*}e^{i(m-n)\theta}]
\end{aligned}\tag{2}
$$
式(2)中$Re[\cdot]$为复数的实数部分，$(\mathbf{W}_kx_n)^{*}$表示$\mathbf{W}_kx_n$的共轭复数，$\theta$为非零常量。进一步表达为
$$
\begin{aligned}
f_{\{q,k\}}(x_m,x_n)=\begin{pmatrix}
cosm\theta&-sinm\theta \\
sinm\theta&cosm\theta
\end{pmatrix}
\begin{pmatrix}
W^{(11)}_{\{q,k\}}&W^{(12)}_{\{q,k\}}\\
W^{(21)}_{\{q,k\}}&W^{(22)}_{\{q,k\}}
\end{pmatrix}
\begin{pmatrix}
x^{(1)}_m\\
x^{(2)}_m
\end{pmatrix}
\end{aligned}\tag{3}
$$
对应的$g$为矩阵。位置信息编码体现在乘积$m\theta$

一般形式

为了把2D的情况泛化到一般形式，作者们把$d$维空间分解成$\frac{d}{2}$个子空间，利用内积线性的优点组合在一起，可见式(4)
$$
\begin{aligned}
f_{\{q,k\}}(x_m,m)=\mathbf{R}^{d}_{\Theta,m}\mathbf{W}_{\{q,k\}}x_m
\end{aligned}\tag{4}
$$
式(4)中
$$
\begin{aligned}
\mathbf{R}_{\Theta,m}^d=\begin{pmatrix}
cosm\theta_1&-sinm\theta_1&0&0&\cdots&0&0\\
0&0&cosm\theta_2&-sinm\theta_2&\cdots&0&0\\
\vdots&\vdots&\vdots&\vdots&\ddots&\vdots&\vdots\\
0&0&0&0&\cdots&cosm\theta_{d/2}&-sinm\theta_{d/2}\\
0&0&0&0&\cdots&sinm\theta_{d/2}&cosm\theta_{d/2}
\end{pmatrix}
\end{aligned}\tag{5}
$$
式(5)为旋转矩阵，$\Theta=\{\theta_i=1000^{-2(i-1)/d},i\in[1,2,\ldots,d/2\}$，原理图可见图1所示。

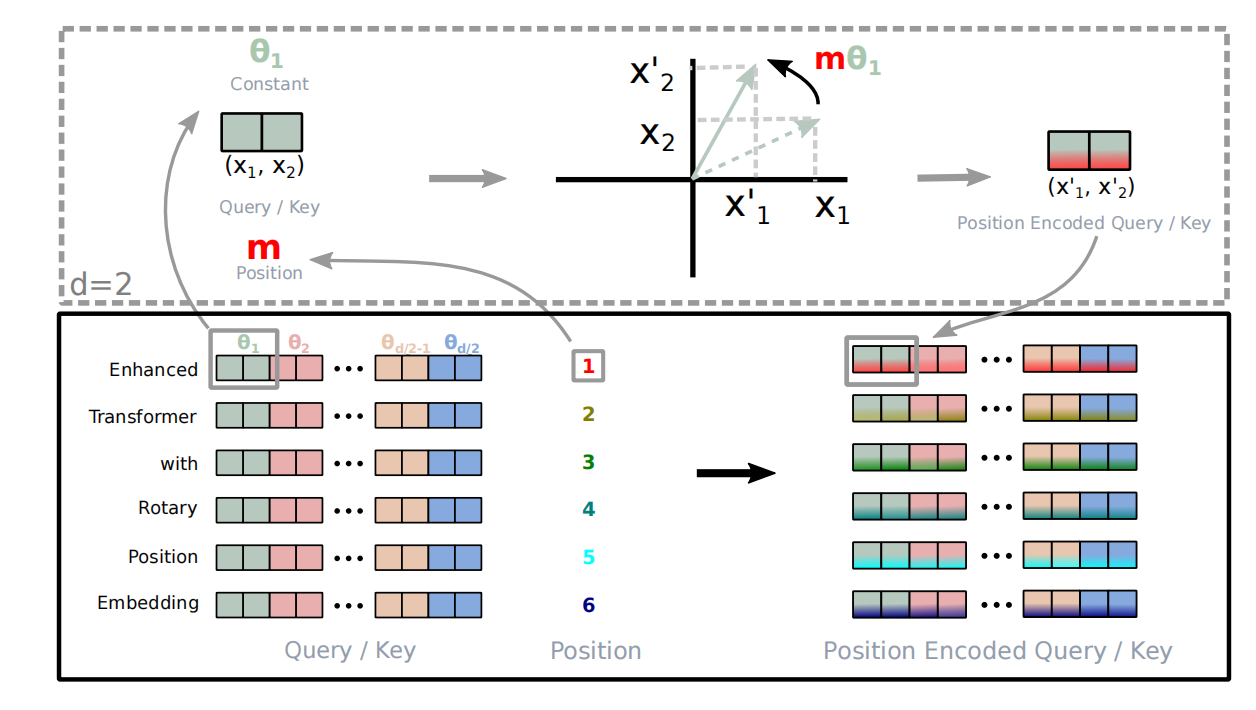
图1 RoPE的原理图

那么，
$$
\begin{aligned}
\mathbf{q}^{T}_m\mathbf{k}_n=(\mathbf{R}_{\Theta,m}^d\mathbf{W}_qx_m)^T(\mathbf{R}_{\Theta,n}^d\mathbf{W}_kx_n)=x^{T}\mathbf{W}_qR_{\Theta,n-m}^d\mathbf{W}_kx_n
\end{aligned}\tag{6}
$$

由于$\mathbf{R}_{\theta}^d$的稀疏性，直接的矩阵相乘效率偏低。因此，作者们建议
$$
\begin{aligned}
\mathbf{R}^d_{\Theta,m}x=
\begin{pmatrix}
x_1\\
x_2\\
x_3\\
x_4\\
\vdots\\
x_{d-1}\\
x_d
\end{pmatrix}
\otimes
\begin{pmatrix}
cosm\theta_1\\
cosm\theta_1\\
cosm\theta_2\\
cosm\theta_2\\
\vdots\\
cosm\theta_{d/2}\\
cosm\theta_{d/2}
\end{pmatrix}+
\begin{pmatrix}
-x_2\\
x_1\\
-x_4\\
x_3\\
\vdots\\
-x_d\\
x_{d-1}
\end{pmatrix}
\otimes
\begin{pmatrix}
sinm\theta_1\\
sinm\theta_1\\
sinm\theta_2\\
sinm\theta_2\\
\vdots\\
sinm\theta_{d/2}\\
sinm\theta_{d/2}
\end{pmatrix}
\end{aligned}\tag{7}
$$

最终，RoPE拥有灵活序列长度、随着位置距离增加的token间衰退的依赖、以及为线性自注意力配备相对位置编码的特性。