QLoRA：量化大语言模型的高效微调

与LoRA相比，QLoRA对预训练模型进行了量化，导致65B参数的模型能够在48GB的GPU上微调，且实现了99.3%的原模型精度。QLoRA的创新点，共有三个，分别是：

• 4-bit NormalFloat Quantization
• Double Quantization
• Paged Optimizers

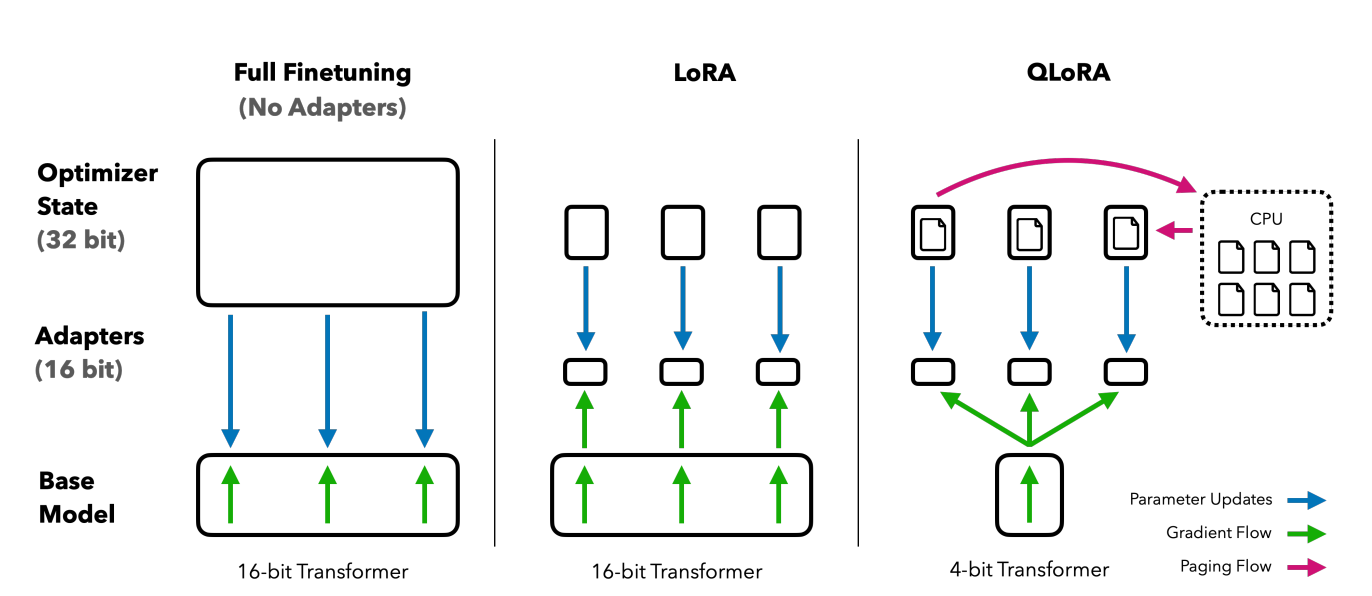
图2 不同微调方法及其内存需求

Quantization

量化是把一个输入从拥有更多信息的表示离散化为拥有更少信息表示的过程。这意味着常常把一个数据类型从更多位转换为更少位，例如：从32位浮点数转换为8位整数。
$$
\begin{aligned}
\mathbf{X}^{Int8}=round(\frac{127}{absmax(\mathbf{X}^{FP32})}\mathbf{X}^{FP32})=round(c^{FP32}\cdot\mathbf{X}^{FP32})
\end{aligned}\tag{2}
$$
式(2)中$c$被称为量化常数。与之相反，去量化为
$$
\begin{aligned}
dequant(c^{FP32},\mathbf{X}^{Int8})=\frac{\mathbf{X}^{Int8}}{c^{FP32}}=\mathbf{X}^{FP32}
\end{aligned}\tag{3}
$$
然而，若一个大幅度值(可以理解为异常值)出现在输入中，那么量化bins就不会很好的被利用。为了阻止这种情况的发生，常把输入分成块，独立地量化这些块。

4-bit NormalFloat Quantization

NormalFloat数据类型建立在Quantile量化的基础之上，这种量化在信息论里属于最优数据类型，确保了量化bin有相同数量的值。Quantile量化需要估计输入tensor的百分位数。然而，这种估计是非常昂贵的。若利用近似算法估计分位数，那么会带来误差。为了避免估计成本高和近似误差的问题。若把输入数据固定为一个分布，那么只需要估计一次百分位数，从而大大降低了成本。

由于神经网络的预训练权重通常属于0均值方差为$\sigma$的正态分布，因此可通过方差缩放的方式使数据变为固定的分布。QLoRA作者把数据分布限制在$[-1,1]$范围内，具体操作步骤为：

• 估计分布$N(0,1)$的$2^{k+1}$个分位数，得到一个$k$位量化优化数据类型。
• 把$k$位量化优化数据类型归一化到$[-1,1]$范围内。
• 利用绝对最大值把输入tensor标准化到$[-1,1]$范围。

只要权重数据范围与数据类型匹配，那么就可以进行量化操作。通常，估计$2^k$个$q_i$值的方式为
$$
\begin{aligned}
q_i=\frac{1}{2}(Q_{X}(\frac{i}{2^{k}+1})+Q_{X}(\frac{i+1}{2^k+1}))
\end{aligned}\tag{4}
$$
式(4)中$Q_{X}$为标准正太分布的分位数函数。对称的$k$位量化无精确的0值表示，这会产生误差。因此，作者们创建了估计$2^{k-1}$个负分位数和$2^{k-1}+1$个正分位数的非堆成方式解决该问题。如图4所示，NF4数据类型的形成步骤。

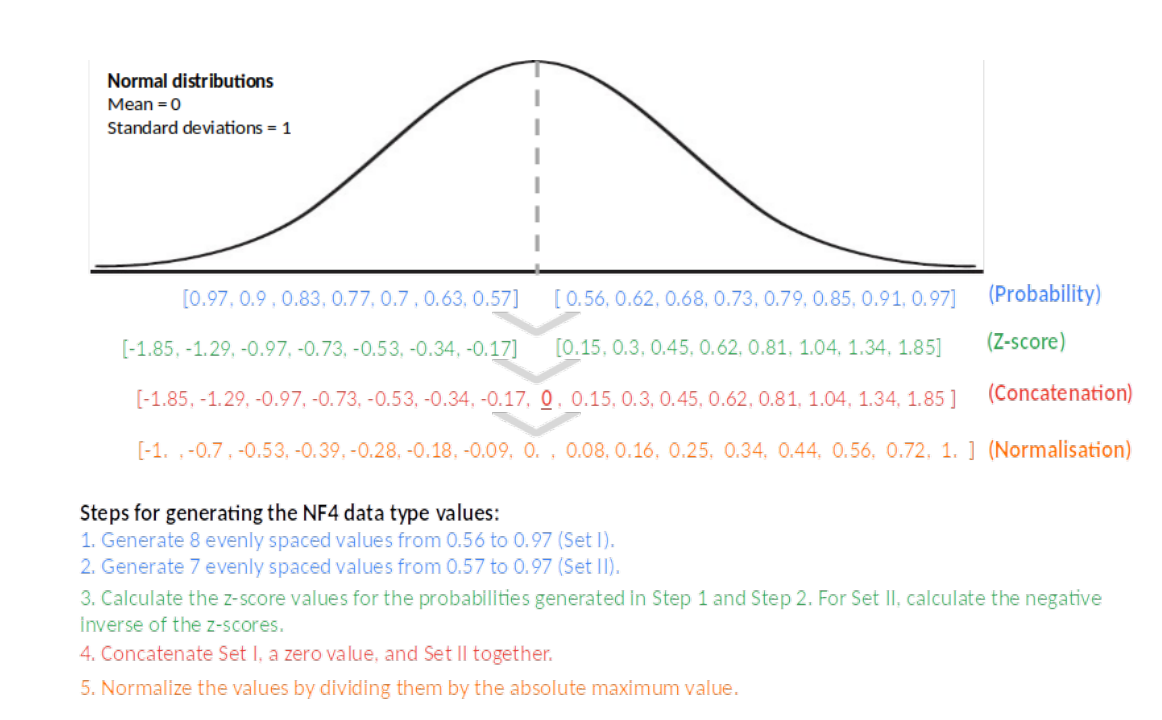
图3 NF4数据形成的步骤

Double Quantization

为了进一步降低内存的需求，对第一次量化的量化常量$c_2^{FP32}$进行了第二次量化。第二次量化产生了量化的量化常量$c_2^{FP8}$和第二级的量化常量$c_1^{FP32}$。最终，使每个参数的内存占用从0.5位变为0.127位，且性能保持不变。

Paged Optimizers

Nvidia的统一内存使CPU与GPU之间零误差的page-to-page的数据迁移，从而避免GPU内存溢出。基于这一特性为优化器状态分配paged内存，自动的在CPU RAM与GPU RAM之间传递数据。

基于以上三个元件，若定义QLoRA为单个线性层，那么可表示为
$$
\begin{aligned}
\mathbf{Y}^{BF16}=\mathbf{X}^{BF16}doubleDequant(c_1^{FP32},c_2^{k-bit},\mathbf{W}^{NF4})+\mathbf{X}^{BF16}\mathbf{L}_1^{BF16}\mathbf{L}_2^{BF16} \\
doubleDequant(c_1^{FP32},c_2^{k-bit},\mathbf{W}^{k-bit})=dequant(dequant(c_1^{FP32},c_2^{k-bit}),\mathbf{W}^{4bit})=\mathbf{W}^{BF16}
\end{aligned}\tag{5}
$$

相关思考

QLoRA论文表示式(5)中$\frac{\partial E}{\partial L_i}$需要计算$\frac{\partial X}{\partial W}$，根据链式法则需要计算的梯度应该不包含$\frac{\partial X}{\partial W}$才对，为什么包含呢？笔者没有思考明白。