一致性模型训练的提升方法
一致性模型已经成为了生成模型的新家族,该模型可以在不需要对抗训练的情况下实现单步高质量数据采样。
一致性模型的训练有两种方式,分别是一致性蒸馏和一致性训练。其中,一致性蒸馏需要预训练一个扩散模型,再把知识蒸馏到一致性模型;一致性训练直接从数据中训练一致性模型,把其视为独立的生成模型家族。对于一致性蒸馏,因其需要预训练扩散模型而导致计算量的增加,且蒸馏方式限制了一致性模型的能力。对于一致性训练所依赖的度量函数LPIPS,主要存在两个缺点,一个是由于LPIPS和FID均在ImageNet数据集上训练,会因特征泄漏产生潜在的评估偏差;另一个是该度量需要需要预训练辅助网络用于特征抽取,从而增加了计算预算。
为了提升一致性训练技术,Improved Techniques for Training Consistency Models作者们不仅对一致性训练的各个模块进行了研究分析,且提出了一系列提升方案。最终,一致性训练在单步采样不仅获得了超越了一致性蒸馏的FID分数,且相较于之前一致性训练获得了$3.5$倍的提升。此外,超越了扩散模型的few-step扩散蒸馏技术的最好模型。通过两步生成,实现了超越一致性蒸馏的FID分数。这些结果战胜了顶级扩散模型,表明一致性模型作为生成模型的独立家族拥有很强的前景。
背景知识
LIPIS
Learned Perceptual Image Path Similarity(LPIPS)是一种通过计算深度神经网络抽取两个patches特征编码之间$l_2$距离以度量相似度的方法。值得注意的是,该项研究证明了假设:感知相似度不是一个独立存在的特殊函数,而是视觉表示的结果,基于该视觉表示可预测世界的重要结构。由此,可知,若利用LIPIS作为目标函数,需要训练一个独立的模型,用于生成图片的低维度表示。
一致性训练的提升技术
如表示1所示,与一致性模型训练的默认选择相比,作者们的改进。
表1 一致性训练设计选择的比较

权重函数,噪音编码,以及Dropout
对于权重函数的改进,其背后的思想是:在更小噪音级别上最小化一致性损失误差对模型性能影响更大,因此应提高对应的权重。简单来说,随着噪音级别的增加,权重应该是降低的。如图1c所示,该权重函数显著的增加了样本质量。
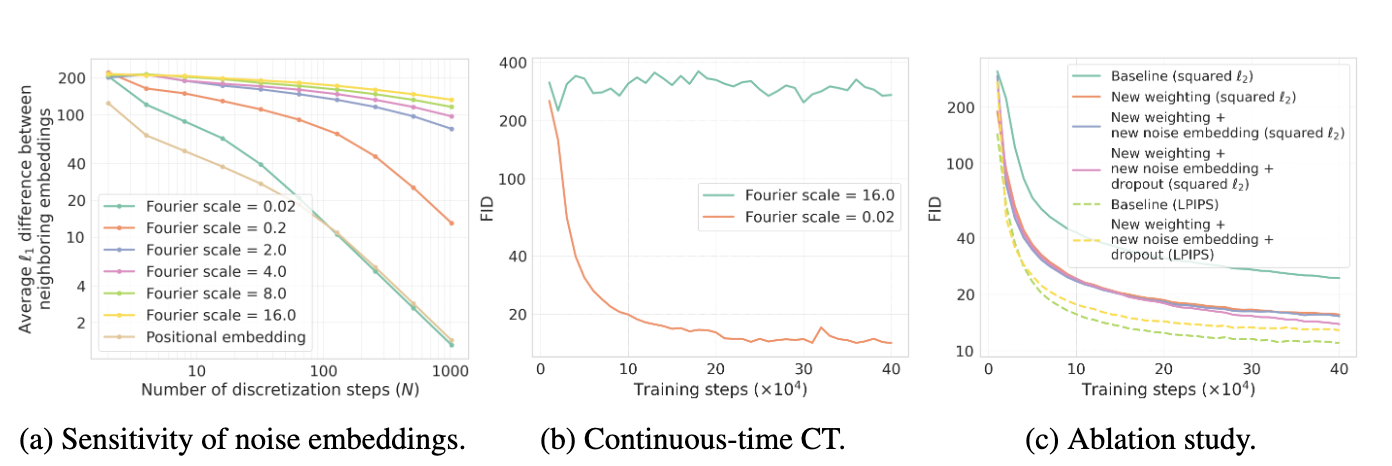
图1 相关实验验证一
在一致性模型中,其作者们利用Fourier编码层和Transformer中位置编码层对噪音级别进行编码。虽然噪音编码对训练信号变化的足够敏感非常重要,但是太敏感可能导致训练的不稳定性,可见图1b所示。为了克服这种不稳定性,一致性模型的作者们利用预训练扩散模型的参数对模型进行初始化。然而,这篇论文的作者们发现,若利用不那么敏感的噪音编码层且Fourier缩放参数变小,那么随机初始化的连续时间一致性训练会拟合。如图1c所示,离散时间一致性训练的Fourier编码层的缩放参数由默认值$16$降为$0.02$,也会带来模型性能的提升。对于ImageNet模型,作者们采用默认的位置编码,这是因为其与缩放参数为$0.02$的Fourier编码拥有相似的敏感度。
Plus:Fourier编码主要用于提高神经网络捕获高频特征的能力。
一致模型训练的默认dropout为$0$,这是因为作者们认为一致性模型比扩散模型的学习难度大,因此不容易过拟合。然而,本文作者们发现,更大的dropout会提升一致模型的样本质量,可见图1c所示。
权重函数和噪音编码层的改进以及增加dropout,可使以$l_2$为损失项的一致性模型的样本质量得到很大的提升。那么,如何提升以LPIPS为损失函数的一致性训练的样本质量呢?作者又进行了其它改进。
从Teacher网络中移除EMA
在介绍度量函数之前,先讲一下作者们对目标函数的指数移动平均$\mu(k)$的改进。通过理论分析和实验验证(可见2a图),发现,$\mu(k)=0$可显著提高模型的性能。其中,图2中Improved表示利用了权重函数、噪音编码、以及dropout的改进。
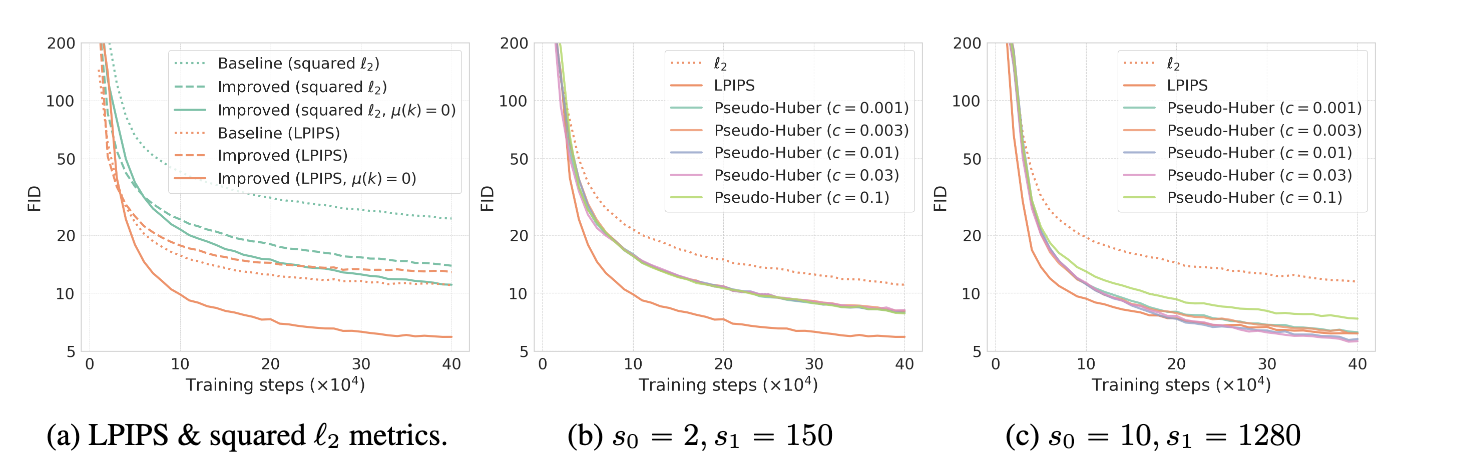
图2 相关实验验证二
Pseudo-Huber度量函数
如图2a所示,虽然这些改进能够使以$l_2$为度量的一致性训练与原始一致性训练相匹配,但是以LPIPS为损失函数的模型性能仍是最优的。由此,作者们引入了Pseudo-Huber为度量的损失函数
$$ \begin{aligned} d(x,y)=\sqrt{\Vert x-y\Vert_2^2+c^2}-c \end{aligned}\tag{1} $$
式中$c\gt0$为可调节的常量。
该度量方式为$l_1$和$l_2$之间的平滑连接,$c$决定了抛物线部分的宽度,可见图3a所示。与$l_0,l_1$以及$l_{\infty}$相比,Pseudo-Huber度量拥有连续且二次可微的特性。
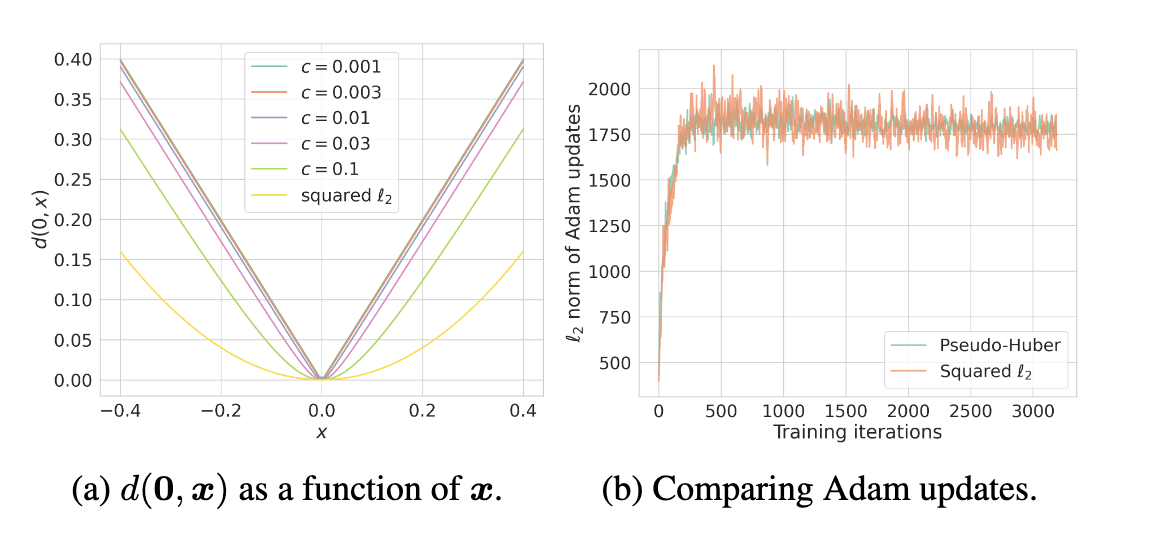
图3 (a) 各种度量函数的形状。(b) Adam优化器中参数更新的$l_2$范数。曲线被重新缩放以具有相同的平均值。与平方$l_2$度量相比,Pseudo-Huber度量的方差较低。
根据图3b,可知,Pseudo-Huber鲁棒性更高,这是因为该度量对异常值时间的惩罚更小。
同时,根据图2,可知,若$s_0=2,s_1=150$变为$s_0=10,s1=1280$以提高离散化步骤数$N(k)$,一致性训练首次超越了以LPIPS为目标函数的模型。此外,图2c中表明$c=0.03$为最优的。作者们建议$c$应该随着$\Vert x-y\Vert_2$而线性的缩放,启发式的方法是$c=0.00054\sqrt{d}$。其中,$d$图片的维度。
离散化步骤的提升课程
根据一致性训练的理论基础,随着$N\to\infty$,一致性训练渐近收敛到目标值。然而,实践中只能选择有限的$N$用于训练一致性模型,由此引入了偏差。为了研究$N$对生成样本质量的影响,作者们利用以上提升技术训练一致性模型,其课程设计为
$$ \begin{aligned} N(k)=min(s_02^{\lfloor\frac{k}{{K}'}\rfloor},s_1)+1,~{K}^{'}=\lfloor\frac{K}{log_2\lfloor s_1/s_0\rfloor+1}\rfloor \end{aligned}\tag{2} $$
在图3b中,被标记为Exp
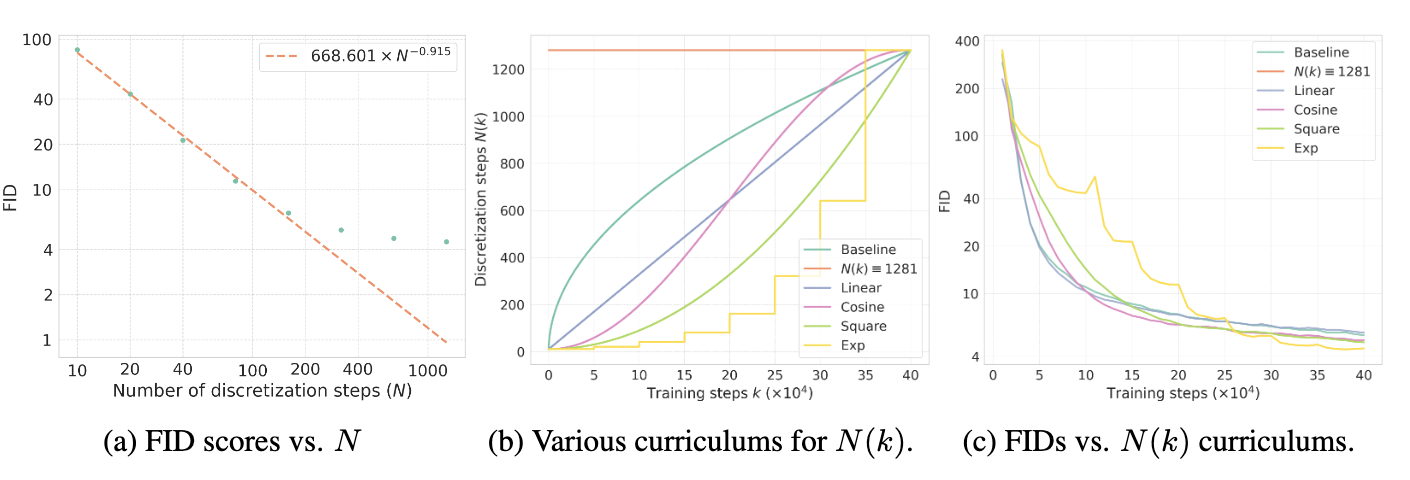
图4 相关实验三
如图3a所示,随着$N$增加,一致性模型样本质量不断提升,且FID分数与$N$之间呈现幂律分布。在一致性训练中,虽然$N$越大偏差降低得越多,但会增加方差。在实验中,作者们发现$N(k)=1281$时,模型在偏差与方差之间保持一个平衡,因此$N(k)$的最大值应不超过$1281$。根据图3c,Exp形式的课程模型性能最佳,因此设定其为标准课程。
提升噪音调度器
在一致模型中,默认的噪音调度为从分布$\mathcal{U}[1,N-1]$中采样一个$i$,再选择$\sigma_i$和$\sigma_{i+1}$计算一致性训练的目标函数。其中,$\sigma_i=(\sigma_{min}^{1/\rho}+\frac{i-1}{N-1}(\sigma_{max}^{1/\rho}-\sigma_{min}^{1/\rho}))^{\rho}$,其对应的采样分布为$p(log\sigma)=\sigma\frac{\sigma^{1/\rho-1}}{\rho(\sigma_{max}^{1/\rho}-\sigma_{min}^{1/\rho})}$
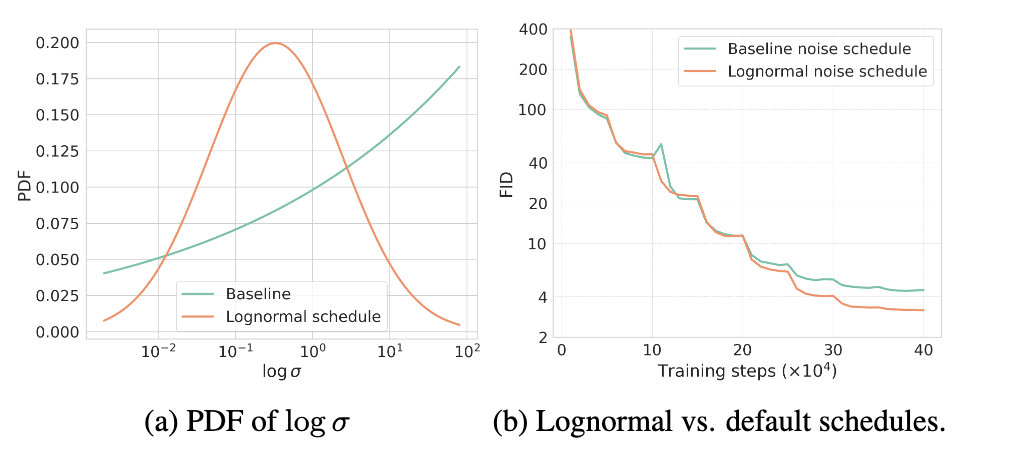
图5 噪音调度的概率密度函数与相关实验
如图5a所示,默认的采样分布对高的$log\sigma$分配了更高的概率密度。实际上,较低的噪音级别应该拥有更大的采样密度,这样才能降低误差累计。由此,作者们采用lognormal分布作为采样噪音级别的概率密度函数,即
$$ \begin{aligned} p(\sigma_i)\propto erf(\frac{log(\sigma_{i+1})-P_{mean}}{\sqrt{2}P_{std}})-erf(\frac{log(\sigma_i-P_{mean})}{\sqrt{2}P_{std}}) \end{aligned}\tag{3} $$
式中$P_{mean}=-1.1,P_{std}=2.0$,erf为误差互补函数$\frac{2}{\sqrt{\pi}}\int_{0}^{x}e^{-t^2}dt$
如图4b所示,lognormal显著提升了样本质量。
引用方法
请参考:
li,wanye. "一致性模型训练的提升方法". wyli'Blog (Nov 2024). https://www.robotech.ink/index.php/archives/671.html
或BibTex方式引用:
@online{eaiStar-671,
title={一致性模型训练的提升方法},
author={li,wanye},
year={2024},
month={Nov},
url="https://www.robotech.ink/index.php/archives/671.html"
}
CC版权: 本篇博文采用《CC 协议》,转载必须注明作者和本文链接