Consistency Models:一致性模型
扩散模型显著地提升了图片、音频、视频生成领域,这种模型依赖迭代的采样过程,从而导致生成速度很慢。为了解决生成慢的问题,一致性模型被提出。这种模型的核心思想是从相同轨迹上任何一点开始采样,最终的输出为一致的,可见图1所示。一致性模型有两种训练方式,分别是蒸馏预训练扩散模型和生成模型的直接训练。通过实验表明这两种方式在one-step和few-step生成上均实现了新SOTA的结果,即一致性模型不仅能够执行单步采样,且拥有迭代性采样的优势。
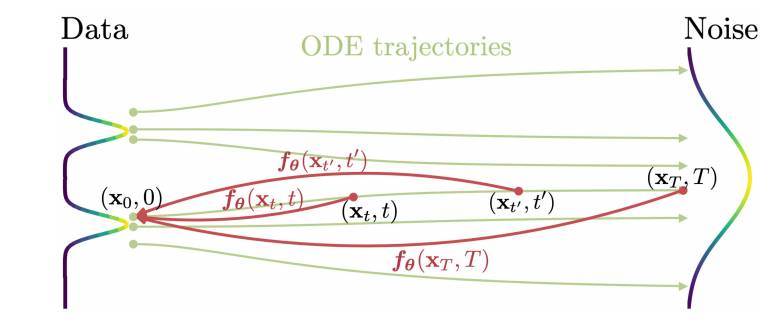
图1 一致性模型学习把PFODE任何轨迹上的点映射到轨迹原点
扩散模型
若$p_{data}(x)$为表示数据分布,扩散模型利用随机微分方程式(1)对数据进行扩散
$$
\begin{aligned} d\mathbf{x}_t=\mu(\mathbf{x}_t,t)dt+\sigma(t)d\mathbf{w}_t
\end{aligned}\tag{1}
$$
式(1)中$t\in[0,T]$,$\mu(\cdot,\cdot)$为漂移系数,$\sigma(\cdot)$为扩散系数,$\{\mathbf{w}_t\}_{t\in[0,T]}$为标准布朗运动。
$\mathbf{x}_t$的分布表示为$p_t(\mathbf{x})$,且$p_0(\mathbf{x})\equiv~p_{data}(\mathbf{x})$。该随机微分方程对应的常微分方程为
$$
\begin{aligned}
d\mathbf{x}_t=[\mu(\mathbf{x}_t,t)-\frac{1}{2}\sigma(t)^2\nabla logp_{t}(\mathbf{x}_t)]dt
\end{aligned}\tag{2}
$$
该常微分方程被称为概率流常微分方程,在时刻$t$采样的解轨迹为$p_t(\mathbf{x})$。
为了使$p_T(\mathbf{x})$接近于高斯分布$\pi(\mathbf{x})=\mathcal{N}(0,T^2I)$,通常设置$\mu(\mathbf{x},t)=0,\sigma(t)=\sqrt{2}(t)$,那么$p_t(x)=p_{data}(x)\otimes\mathcal{N}(0,T^2I)$。同时,基于分数匹配训练一个分数模型$s_{\phi}(t)\approx\nabla logp_t(x)$,那么式(2)可为
$$
\frac{d\mathbf{x}}{dt}=-ts_{\phi}(\mathbf{x}(t),t)
$$
该式被称为概率流常微分方程的实验性估计。
在生成数据时,从分布$\hat{\mathbf{x}}_T\sim\pi=\mathcal{N}(0,T^2I)$开始采样,利用数值ODE求解器获得解轨迹$\{\hat{\mathbf{x}}\}_{t\in [0,T]}$ 通常为了避免数值不稳定性,利用$\{\hat{\mathbf{x}}\}_{\epsilon}$代替$\{\hat{\mathbf{x}}\}_{0}$近似真实数据分布。
一致性模型
一致性模型的提出主要受到连续时间扩散模型理论的启发。接下来,对一致性模型的定义、参数化、以及采样进行详细的介绍。
定义:
给定式(2)的解轨迹,定义一致性函数为$f:(\mathbf{x}_t,t)\to\mathbf{x}_{\epsilon}$。该函数具有自一致性特性:相同概率流常微分方程轨迹上任意一对$(\mathbf{x}_t,t)$的输出是一致的,即$\forall {t}'\in[\epsilon,T]$,其$f(\mathbf{x}_t,t)=f(\mathbf{x}_{{t}'},{t}')$
一致性模型$f_{\theta}$的目标是:从数据中学习自一致性特性,以估计一致性函数$f$
该定义神经常微分方程下的神经流相似,不同的是一致性模型并不强制可逆。
参数化
对于一致性函数$f(\cdot,\cdot)$,其$f(\mathbf{x}_{\epsilon},\epsilon)=\mathbf{x}_{\epsilon}$,即$f(\cdot,\epsilon)$为身份函数。该约束也被称为边界条件,所有的一致性模型都满足该边界条件。对于基于深度神经网络$F_{\theta}(\mathbf{x},t)$的一致性模型,有两种实现边界条件的方式。第一种方法为:
$$
\begin{aligned}
f_{\theta}(\mathbf{x},t)=\begin{cases}
\mathbf{x} & t=\epsilon \\
F_{\theta}(\mathbf{x},t) & t\in(\epsilon,T]
\end{cases}
\end{aligned}\tag{3}
$$
第二种方式是利用跳连接参数化一致性模型:
$$
\begin{aligned}
f_{\theta}(\mathbf{x},t)=c_{skip}(t)\mathbf{x}+c_{out}(t)F_{\theta}(\mathbf{x},t)
\end{aligned}\tag{4}
$$
其中,$c_{skip}(t)$和$c_{out}(t)$为可微分函数且$c_{skip}(\epsilon)=1,c_{out}(\epsilon)=0$
由于式(4)的参数化方式与EDM扩散框架有很强的相似之处,因此可直接借鉴扩散模型的设计方法,这也是采用第二种方式对一致性模型进行参数化的原因。
在EDM中,$c_{skip}(t),c_{out}(t)$的设置为
$$
\begin{aligned}
c_{skip}(t)=\frac{\sigma_{data}^2}{t^2+\sigma_{data}^2}\qquad c_{out}(t)=\frac{\sigma_{data}t}{\sqrt{\sigma_{data}^2+t^2}}
\end{aligned}
$$
式中$\sigma_{data}=0.5$
为了满足边界条件,作者们把它修改为
$$
\begin{aligned}
c_{skip}(t)=\frac{\sigma_{data}^2}{(t-\epsilon)^2+\sigma_{data}^2}\qquad c_{out}(t)=\frac{\sigma_{data}(t-\epsilon)}{\sqrt{\sigma_{data}^2+t^2}}
\end{aligned}
$$
采样
一致性模型的单步采样是:先从初始分布$\hat{\mathbf{x}}_T\sim\mathcal{N}(0,T^2I)$中采样,再利用一致性模型生成数据$\hat{\mathbf{x}}_{\epsilon}=f_{\theta}(\hat{\mathbf{x}}_T,T)$
对于多步采样可见算法1

通过蒸馏训练一致性模型
与 Progressive Distillation 蒸馏相似,一致性蒸馏训练的模型性能优于扩散模型,且均可单步迭代生成样本。
一致性蒸馏是对预训练的分数模型$s_{\phi}(\mathbf{x},t)$进行蒸馏得到一致性模型。对于离散化的时间窗口$[\epsilon,T]$,被分为$N-1$子区间,即$t_1=\epsilon\lt t_2\lt\ldots\lt t_{N}=T$。其中,边界的确定方式遵循EDM扩散框架,即$t_i=({\epsilon}^{\frac{1}{\rho}}+\frac{i-1}{N-1}(T^{\frac{1}{\rho}}-\epsilon^{\frac{1}{\rho}}))^{\rho}$,即噪音调度方法,且$\rho=7$。
若$N$足够大,那么可通过数值ODE求解器,由$\mathbf{x}_{t_{n+1}}$得到$\mathbf{x}_{t_n}$
$$
\begin{aligned}
\hat{\mathbf{x}}_{t_n}^{\phi}:=\mathbf{x}_{t_{n+1}}+(t_n-t_{n+1})\Phi(\mathbf{x}_{t_{n+1}},t_{n+1};\phi)
\end{aligned}\tag{5}
$$
其中,$\Phi(\cdots;\phi)$表示应用于PF ODE的单步ODE求解器更新函数。若求解器为欧式求解器,那么$\Phi(\mathbf{x},t;\phi)=-t\mathbf{s}_{\phi}(\mathbf{x},t)$
根据,基于随机微分方程的扩散模型中理论可知,每个SDE
$$
\begin{aligned}
d\mathbf{x}_t=\mu(\mathbf{x}_t,t)dt+\sigma(t)d\mathbf{w}_t
\end{aligned}\tag{6}
$$
均对应一个PF ODE
$$
\begin{aligned}
d\mathbf{x}_t=[\mu(\mathbf{x}_t,t)-\frac{1}{2}\sigma(t)^2\nabla logp_t(\mathbf{x}_t)]
\end{aligned}\tag{7}
$$
因此,可按照ODE轨迹进行采样,先从数据分布中采样$\mathbf{x}\sim p_{data}$,再对数据$\mathbf{x}$增加噪音,最终可采样出一对数据点$(\hat{\mathbf{x}}_{t_n}^{\phi},\mathbf{x}_{t_{n+1}})$。确切的说,从SDE转换密度$\mathcal{N}(\mathbf{x},t_{n+1}^2,I)$采样出$\mathbf{x}_{t_{n+1}}$,再根据式(5)利用数值ODE求解器的离散化步骤采样出$\hat{\mathbf{x}}_{t_{n}}^{\phi}$。由此,可通过最小化一致性模型在数据点对$(\hat{\mathbf{x}}_{t_n}^{\phi},\mathbf{x}_{t_{n+1}})$上输出差距的方式,进行蒸馏。
定义1:
一致性蒸馏损失为
$$
\begin{aligned}
\mathcal{L}^N_{CD}(\theta,{\theta}^{-};\phi)=\mathbb{E}[\lambda(t_n)d(f_{\theta}(\mathbf{x}_{t_{n+1}},t_{n+1}),f_{\theta^{-}}(\hat{\mathbf{x}}_{t_n}^{\phi},t_n))]
\end{aligned}\tag{8}
$$
式(8)是关于$\mathbf{x}\sim p_{data},n\sim\mathcal{U}[\![1,N-1]\!],\mathbf{x}_{t_{n+1}}\sim\mathcal{N}(\mathbf{x};t_{n+1}^2I)$求期望。其中,$\mathcal{U}[\![1,N-1]\!]$表示关于$\{1,2,\ldots,N-1\}$的均匀分布,$\lambda(\cdot)\in\mathbb{R}^{+}$为正整数权重函数,$\theta^{-}$表示优化过程中$\theta$的移动平均,$d(\cdot,\cdot)$为度量函数。同时,对于$\forall\mathbf{x},\mathbf{y}:d(\mathbf{x},\mathbf{y})\ge0$,且只有$\mathbf{x}=\mathbf{y}$时$d(\mathbf{x},\mathbf{y})=0$
在实验中,作者们利用$d(\mathbf{x},\mathbf{y})=\Vert\mathbf{x}-\mathbf{y}\Vert_2^2$,$d(\mathbf{x},\mathbf{y})=\Vert\mathbf{x}-\mathbf{y}\Vert_1$,以及LPIPS作为度量函数;对于所有任务和数据集,$\lambda\equiv 1$表现较好;利用随机梯度下降更新参数$\theta$,$\theta^{-}$利用指数移动平均进行更新。基于蒸馏的一致性模型训练,可见算法2

与强化学习相对照,$\theta^{-}$被称为目标网络,采用指数移动平均的方式更新,有利于模型稳定的训练。
一致性模型的直接训练
对于一致性蒸馏,需要预训练分数函数$\mathbf{s}_{\phi}(\mathbf{x},t)$近似真实函数$\nabla logp_t(\mathbf{x})$。然而,该预训练模型可完全利用无偏估计器替代
$$
\begin{aligned}
\nabla logp_t(\mathbf{x}_t)=-\mathbb{E}[\frac{\mathbf{x}_t-\mathbf{x}}{t^2}\vert\mathbf{x}_t]
\end{aligned}\tag{9}
$$
其中,$\mathbf{x}\sim p_{data}$,$\mathbf{x}_t\sim\mathcal{N}(\mathbf{x};t^2I)$。
在利用Euler作为ODE求解器且$N\to\infty$时,该无偏估计器足以替换预训练扩散模型。一致性训练算法,可见算法3

同时,为了提升实际表现,作者们提出训练过程中Progressively增加$N$。这是因为在$N$较小时,一致性训练损失的方差小偏差大,从而有利于训练初期的快速拟合;在$N$较大时,一致性训练损失的方差大偏差小,这是训练快结束时期待的结果。总的来说这种方式有利于训练的稳定性。
在整个实验中,作者们设计的调度函数为
$$
\begin{aligned}
N(k)=\lceil\sqrt{\frac{k}{K}((s_1+1)^2-s_0^2)+s_0^2}-1\rceil+1 \\
u(k)=exp(\frac{s_0log\mu_0}{N(k)})
\end{aligned}
$$
式中$K$为训练迭代的总次数,$s_0$为初始离散化步骤,$s_1\gt s_0$表示训练结束时的离散化步骤数的目标值,$\mu_0$为训练开始时EMA衰退率。
引用方法
请参考:
li,wanye. "Consistency Models:一致性模型". wyli'Blog (Jun 2024). https://www.robotech.ink/index.php/archives/523.html
或BibTex方式引用:
@online{eaiStar-523,
title={Consistency Models:一致性模型},
author={li,wanye},
year={2024},
month={Jun},
url="https://www.robotech.ink/index.php/archives/523.html"
}