相似性度量FID的原理

Fr'echet Inception Distance是一种利用Fr'echet Distance计算生成图片与真实图片相似度的度量工具。

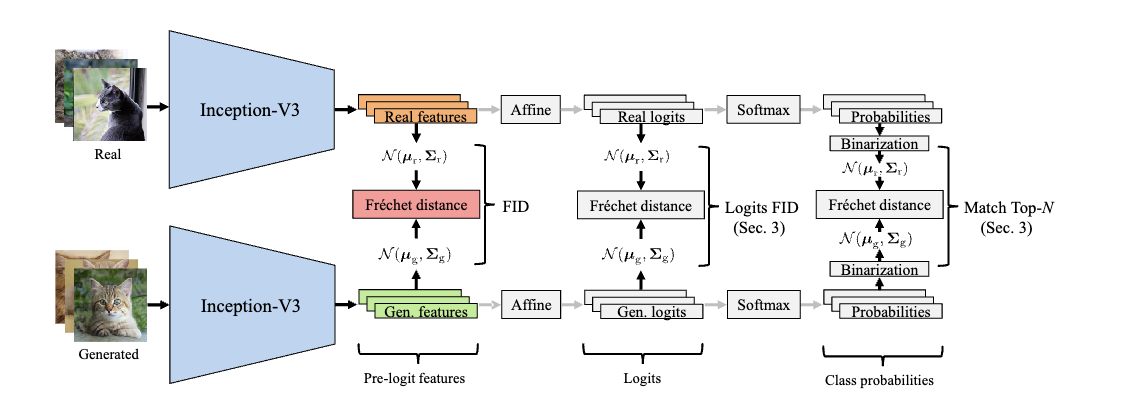
图1 FID原理概览

如图1所示，FID核心思想是：把真实图片和生成图片嵌入到视觉相关的特征空间，且计算两个分布之间的Fr'echet距离。实践中，特征空间为网络的倒数第二层输出，真实图片编码与生成图片编码的分布独立地利用多变量高斯分布近似。由此，两者的距离为
$$
\begin{aligned}
FID(\mu_{r},\Sigma_{r},\mu_g,\Sigma_g)=\Vert\mu_r-\mu_g\Vert_2^2+Tr(\Sigma_r+\Sigma_g-2(\Sigma_r\Sigma_g)^{\frac{1}{2}})
\end{aligned}
$$
式中$(\mu_r,\Sigma_r)$和$(\mu_g,\Sigma_g)$分别为真实数据和生成数据的样本均值与协方差，$Tr(\cdot)$为矩阵的迹。在FID计算时，只考虑pre-logit特征空间，其它的空间是FID的可替代计算方法。

其中，Fr'echet距离是一种曲线之间相似性的度量方法。

Fr'echet距离的定义：

$S$为一个度量空间，曲线$A$为单位区间到$S$的连续性映射，即：$A:[0,1]\to S$。一个区间$[0,1]$的重参数化$\alpha$是一个连续的非递减的映射：$[0,1]\to[0,1]$

若$A$与$B$为空间$S$中两个曲线，那么两者的距离为
$$
\begin{aligned}
F(A,B)=\underset{\alpha,\beta}{inf}~\underset{t\in[0,1]}{max}\{d(A(\alpha(t)),B(\beta(t)))\}
\end{aligned}
$$
$d$为$S$的距离函数。

较为形象的理解：若一个人在一条有限曲线路径上遛狗，狗在另一条曲线上行走。两者均可变化速度以保持皮带的松弛，且均不可向后移动。两条曲线Fr'echet距离为两者均走完各自路径所需的最短皮带长度。若参数$t$为时间，那么$A(\alpha(t))$为狗的位置，$B(\beta(t))$为主人的位置，皮带的长度为时刻$t$两者位置的距离。关于$[0,1]$所有可能重参数化的极小值对应于选择一条最大皮带长度为最小的路径。$\alpha$和$\beta$非递减为两者均不能后退。

那么，若利用多变量高斯分布对特征进行重参数化，计算两者Fr'echet Distance可得FID。其中，高斯分布的均值和协方差为具有相同属性图片编码的统计值。

FID理论很优美，但也存在不足之处。论文The Role of ImageNet Classes in Fréchet Inception Distance中作者们表明：由于FID的特征空间与ImageNet数据类别的空间非常接近，因此模型可通过调整生成图片与真实图片在该特征空间的Top-N分类直方图，就可以降低FID分数。然而，该分数的降低不是生成图片与真实图片更接近生成的，那么该度量方法具有一定的欺骗性。