RL中基于状态-动作的基线降低方差的幻觉

对于基于策略梯度算法估计梯度，常用的减少方差的方法是$Q$函数与只依赖于状态的基线做差，得到优势函数。这种方式可以明显降低方差，且不引入偏差。文献[2],[3],[4],[5],[6]对基于基线的方法进行了扩展，把依赖于状态的基线变为依赖于状态-动作的基线，实验表明其性能超越只依赖状态的基线。为了理解基于状态-动作的基线降低方差的机制，文献[1]对这类基线进行了研究。同时，也提出了一些无偏差的方差降低方法。

对于只依赖于状态的基线，策略梯度的估计器可见式(1)；对于依赖于状态-动作的基线，策略梯度的估计器可见式(2)。
$$
\begin{aligned}
\hat{g}(s,a,\tau)=(\hat{A}(s,a,\tau)-\phi(s))\nabla log\pi(a\vert s)
\end{aligned}\tag{1}
$$

$$
\begin{aligned}
\hat{g}(s,a,\tau)=(\hat{A}(s,a,\tau)-\phi(s,a))\nabla log\pi(a\vert s)+\nabla\mathbb{E}_{a\vert s}[\phi(s,a)]
\end{aligned}\tag{2}
$$

策略梯度方差分解

接下来，先根据方差计算规则，分解一下式(2)的方差$\Sigma:=Var_{s,a,\tau}(\hat{g})$
$$
\begin{aligned}
\Sigma=\mathbb{E}_s[Var_{a,\tau\vert s}((\hat{A}(s,a,\tau)-\phi(s,a))\nabla log\pi(a\vert s))]+Var_s\mathbb{E}_{a,\tau\vert s}[\hat{A}(s,a,\tau)\nabla log{\pi(a\vert s)}]
\end{aligned}\tag{3}
$$
式(3)第一项可进一步分解
$$
\begin{aligned}
& \mathbb{E}_s[Var_{a,\tau\vert s}((\hat{A}(s,a,\tau)-\phi(s,a))\nabla log\pi(a\vert s))] \\
& = \mathbb{E}_{s,a}[Var_{\tau\vert s,a}(\hat{A}(s,a,\tau)\nabla log{\pi(a\vert s)})]+\mathbb{E}_s[Var_{a\vert s}((\hat{A}(s,a)-\phi(s,a))\nabla log{\pi(a\vert s)})]
\end{aligned}\tag{4}
$$
式(4)中$\hat{A}(s,a)=\mathbb{E}_{\tau\vert s,a}[\hat{A}(s,a,\tau)]$

合并式(3)与式(4)可得
$$
\begin{aligned}
\Sigma &= \underset{\Sigma_{\tau}}{\underbrace{\mathbb{E}_{s,a}[Var_{\tau\vert s,a}(\hat{A}(s,a,\tau)\nabla log{\pi(a\vert s)})]}} \\
& + \underset{\Sigma_a}{\underbrace{\mathbb{E}_s[Var_{a\vert s}((\hat{A}(s,a)-\phi(s,a))\nabla log{\pi(a\vert s)}]}} \\
& + \underset{\Sigma_s}{\underbrace{Var_s(\mathbb{E}_{a\vert s}[\hat{A}(s,a)\nabla log\pi(a\vert s)])}}
\end{aligned}\tag{5}
$$
根据式(5)，可知，只有$\Sigma_a$包含$\phi$，且方差最小化的$\phi(s,a)=\hat{A}(s,a)$。同时，也可以了解到在线梯度估计的方差产生于

• $\Sigma_s$显示只收集到了少量状态的数据。
• $\Sigma_a$显示每个状态下只采样了一个动作。
• $\Sigma_\tau$只执行了单一的路径轨迹。

方差$\Sigma_a$的量级决定了依赖于状态-动作的最优基线的有效性。若式(5)中第二项利用一个只依赖于状态基线$\Sigma_a^{\phi(s)}$表示，那么策略梯度估计器的方差为$\Sigma_a^{\phi(s)}+\Sigma_{\tau}+\Sigma_{s}$。同时，若$\phi(s,a)$是最优的，那么$\Sigma_a$消失，方差变为$\Sigma_{\tau}+\Sigma_s$。因此，当$\Sigma_a^{\phi(s)}$相对大于$\Sigma_{\tau}+\Sigma_s$时，最优的依赖于状态-动作的基线才会有益。

经验方差计算

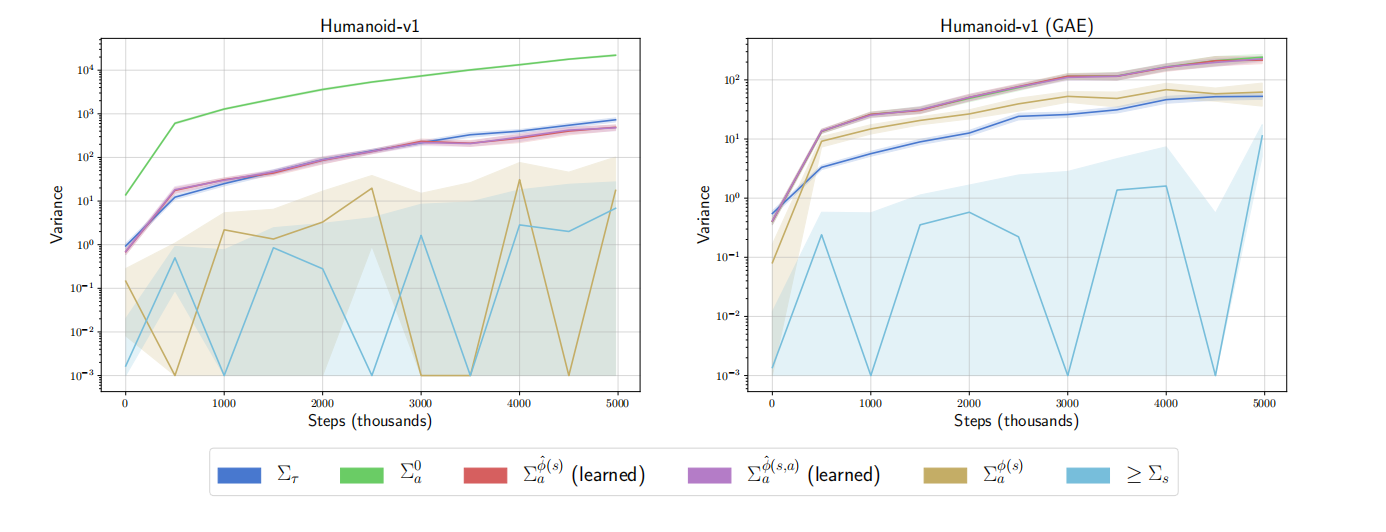
图1中左图中以$\sum_t\gamma^t r^t$方式计算$\hat{A}(s,a)$，而右图中以GAE的方式计算$\hat{A}(s,a)$，从而分别得到不同方差项的结果。其中，$\phi(s)$设置为$\mathbb{E}_a[\hat{A}(s,a)]$，$\phi(s,a)$设置为$\hat{A}(s,a)$；"learned"标签表示基于学习的函数近似，而不是直接使用$\phi$。同时，由于$\phi(s,a)=\hat{A}(s,a)$时，$\Sigma_a^{\phi(s,a)}=0$，所以图1中没有显示该项。

分析图1，可得如下结论：

• 在基于GAE计算优势函数的实验中，发现，依赖于状态-动作的最优先知基线理论上可以提升学习性能。
• 根据函数近似器$\phi$的结果，可知，依赖于状态的函数近似器与依赖于状态-动作的函数近似器产生相似的方差，但是方差高于基于先知$\phi$的结果。从而，表明，实践中基于状态-动作的基线相比于基于状态的基线并不会提升学习性能。

方差降低的原理

优势函数标准化

文献[2]中Q-Prop算法与文献[6]中IPG算法均表明无偏差，该两种算法在实现时均利用了一个自适应标准化。跟确切的说，估计器的标准化为
$$
\begin{aligned}
\hat{g}(s,a,\tau)=\frac{1}{\hat{\sigma}}(\hat{A}(s,a,\tau)-\phi(s,a)-\hat{\mu})\nabla{log\pi(a\vert{s})}+\nabla\mathbb{E}[\phi(s,a)]
\end{aligned}\tag{6}
$$
式(6)中$\hat{\mu}$和$\hat{\sigma}$是基于小批量数据的统计估计值。很明显，这偏离了原本的方法。

值得一提的是，文献[6]中也分析了式(2)中第一项与被称为偏差纠正项的第二项权重不同时，引入的偏差。这种权重的不同可视为方差与偏差之间的妥协。文献[6]中分析的是引入的权重，而不是标准化引入的自适应权重。然而，该显式权重被标准化完全抵消了，因此文献[2]与文献[6]均引入了一个自适应方差与偏差妥协的项。

如图2所示，本文作者们也对无偏差的$Q-Prop$、有偏差的$Q-Prop$、以及TRPO算法进行了评估。

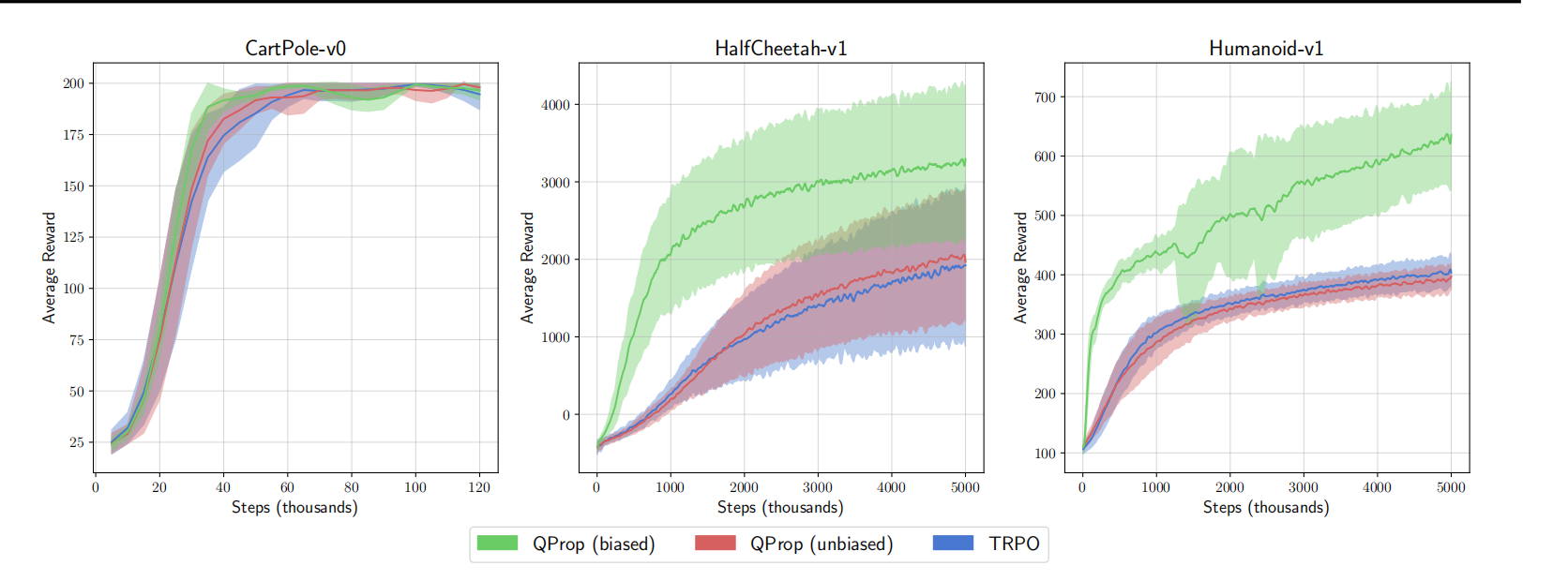
根据图2，可知，异步标准化引入的方差-偏差妥协项的确能够提升算法性能。

价值函数拟合的不充分

文献[4]中，作者们表明在连续控制领域依赖于状态-动作的基线比依赖于状态的基线更能够降低方差。然而，本文作者认为这是因为价值函数拟合不足的原因。为了进行说明，进行了如下分析:

若$\hat{V}(s)=V^{\pi}(s)$，那么GAE估计器的均值为0，这表明价值函数拟合足够的情况下依赖于状态的基线是不必要的。然而，现实中价值函数拟合不足时常出现，因此会出现依赖于状态-动作的基线与依赖于状态的基线具有相似的结果。

基线拟合中样本的再利用

文献[3],[4]中利用on-policy样本对依赖于状态-动作的基线进行拟合。具体来说，要么拟合Monte-Carlo回报，要么最小化梯度估计器方差的近似。这种基于当前批次数据拟合基线，再用更新后的基线得到梯度估计器会产生一个有偏差的梯度。虽然这种方式降低了方差，但是很难分析其引入的偏差。这是因为这种偏差被函数拟合器的正则化所影响。

本文作者基于文献[4]Stein算法的开源代码，评估了三个变体，分别是：计算策略梯度之后无偏的方式拟合依赖于状态-动作的基线、计算策略梯度之后无偏的方式拟合依赖于状态的基线、以及代替重要性权重采样的基于当前批次的额外数据评估偏差纠正项，其结果如图3所示。

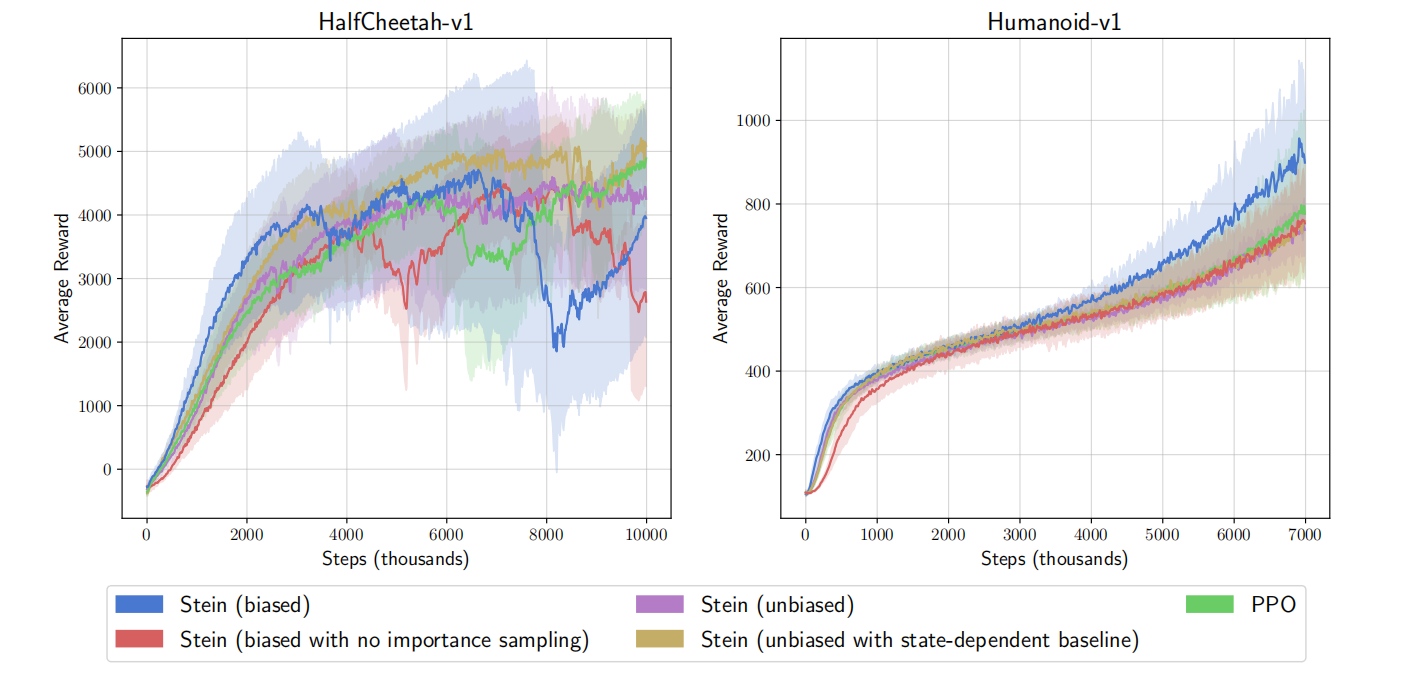
根据图3可知，额外样本通过避免重要性采样的方式降低了方差，但是由于基线对当前批次数据的过拟合降低了性能。

窗口感知的价值函数

在之前的部分中提到价值函数拟合不足产生误导的结果，为了修正这种缺陷，提出了一种新的窗口感知的价值函数参数化方法。与依赖于状态-动作基线相比，这种修改不会引入偏差。

具体来说，价值函数拟合起输出两个值，分别是：$\hat{V}_1(s)$和$\hat{V}_2(s)$，价值函数的估计为
$$
\begin{aligned}
\hat{V}(s_t)=(\sum_{i=t}^T{\gamma}^i)\hat{V}_1(s_t)+\hat{V}_2(s_t)
\end{aligned}\tag{7}
$$
式(7)中$T$为episode的最大长度。

从概念上讲，$\hat{V}_1(s)$被认为预测关于折扣时间平均化的折扣回报，而$\hat{V}_2(s)$被认为依赖于状态的偏移量。如图4所示，本文作者们基于TRPO进行的实验。

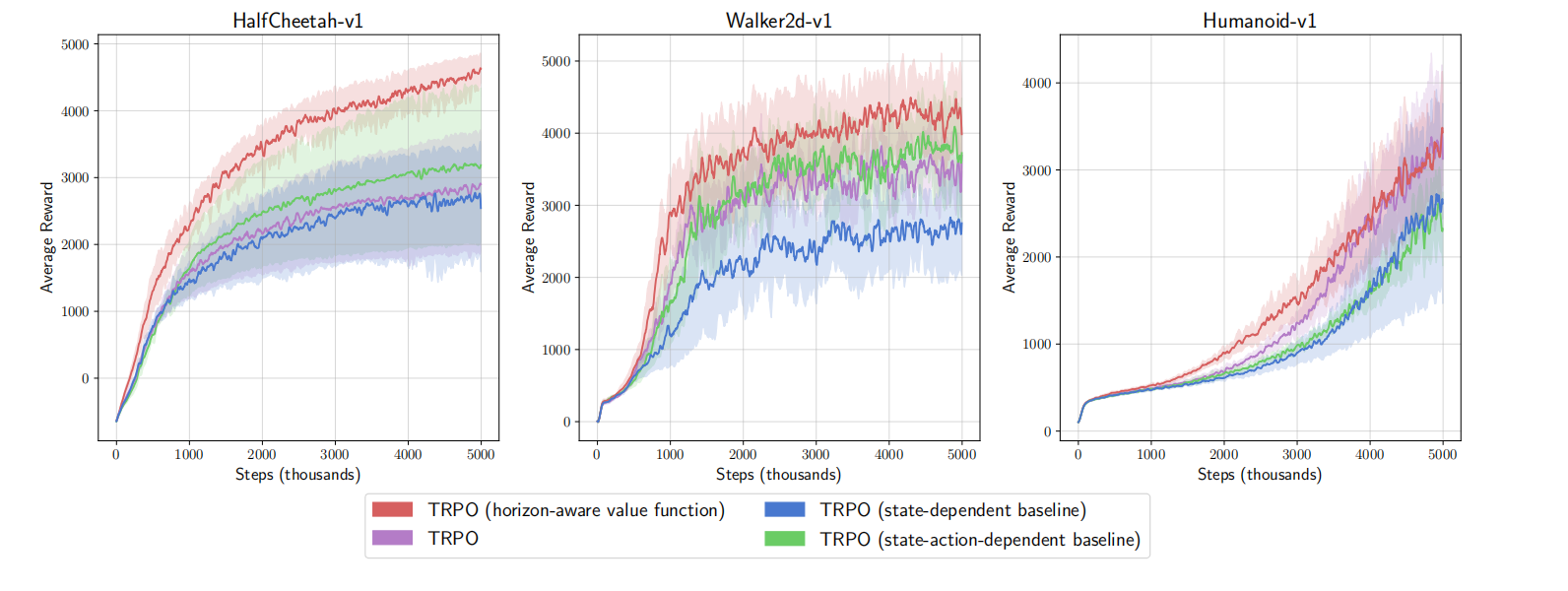
根据实验结果可知，基于窗口感知的价值函数估计的确会实现性能的提升，而且不会引入方差。

参考文献

[1] Tucker, George, et al. "The mirage of action-dependent baselines in reinforcement learning." International conference on machine learning. PMLR, 2018.

[2] Gu, Shixiang, et al. "Q-prop: Sample-efficient policy gradient with an off-policy critic." arXiv preprint arXiv:1611.02247 (2016).

[3] Grathwohl, Will, et al. "Backpropagation through the void: Optimizing control variates for black-box gradient estimation." arXiv preprint arXiv:1711.00123 (2017).

[4] Liu, Hao, et al. "Action-depedent Control Variates for Policy Optimization via Stein's Identity." arXiv preprint arXiv:1710.11198 (2017).

[5] Wu, Cathy, et al. "Variance reduction for policy gradient with action-dependent factorized baselines." arXiv preprint arXiv:1803.07246 (2018).

[6] Gu S S, Lillicrap T, Turner R E, et al. Interpolated policy gradient: Merging on-policy and off-policy gradient estimation for deep reinforcement learning[J]. Advances in neural information processing systems, 2017, 30.