MCAC：稀疏奖励环境下Monte-Carol增强的Actor-Critic算法

现实世界中，强化学习算法面对的往往是稀疏奖励环境。在稀疏奖励环境中，对探索产生了很大的挑战。这是因为稀疏奖励函数使智能体无法有意义的区分不同策略之间的区别。对稀疏奖励函数问题，处理该问题常见的方法是利用专家演示数据提供状态空间中高奖励区域的初始信号。然而，之前基于演示的方式往往使算法本身变得很复杂，且增加了实施以及调节超参数的难度。文献[1]作者们另辟蹊径，提出了MCAC算法了，既没有过多的增加模型复杂性，也没有增加额外的超参数。

MCAC算法背后的核心思想是：鼓励智能体在次优轨迹的邻域内保持初始乐观，且随着算法学习不断减少乐观以鼓励探索新的行为。具体实现方式为：MCAC 中引入了两个修改，分别是基于专家演示数据初始化replay buffer和选择TD-learning中价值估计的目标值与Monte-Carlo价值估计目标值之间的最大值作为Q值的目标值。之所以利用Monte-Carlo价值估计，这是因为MC方法更能够高效的捕获长期奖励信息，使奖励信息得到更快的传递。

Monte-Carlo增强的Actor-Critic

MCAC算法

如图1所示，MCAC算法伪代码。

图1中式(5.2)对应于本文的式(2)，式(5.4)对应于本文的式(4)。

TD-Learning由于基于时序差分的方式，很难传播奖励信息，所以在学习早期的价值估计很低。另一方面，Monte-Carlo方式的目标值虽然很容易捕获长期奖励，但是对表现稍差的轨迹会严重的低估$Q$值，即MC为无偏估计而方差大。与MC不同，TD-Learning属于有偏估计但方差低。在MCAC算法，选择MC目标值与TD-Learning目标值之间的最大值能够降低MC对高价值区域的邻域的过度低估问题。

MCAC算法的实际实现

MCAC可被看成对actor-critic类算法的包装。MCAC算法首先基于次优演示数据$\mathcal{D}_{offline}$初始化Replay Buffer。然后，在每个episode，收集一个完整轨迹$\tau^i$，轨迹中的第$j$个转换为$(s_j^i,a_j^i,s_{j+1}^i,r_j^i)$。接下来，基于任何actor-critic方法学习$Q$函数的近似$Q_{\theta}(s_t,a_t)$。对于给定的转换$\tau_j^{i}=(s_j^i,a_j^i,s_{j+1}^i,r_j^i)\in\tau^i\subsetneq\mathcal{R}$，其损失函数为
$$
\begin{aligned}
J(\theta)=l(Q_{\theta}(s_j^i,a_j^i),Q^{target}(s_j^i,a_j^i))
\end{aligned}\tag{1}
$$
为了实现MCAC，文献[1]作者们首先校准了MC目标值。MC目标值校准的前提假设是：最后观测到的奖励值会一直重复，具体可见式(2)
$$
\begin{aligned}
Q^{target}_{MC-\infty}(s_j^i,a_j^i)=\gamma^{T-j+1}\frac{r^i_T}{1-\gamma}+\sum_{k=j}^T\gamma^{k-j}r(s_k^i,a_k^i)
\end{aligned}\tag{2}
$$

这种校准是有偏差的，但影响不大。这是因为时间$T$步之后的折扣$\gamma$使其奖励对时间步j的影响很小。

MCAC中$Q$函数的目标值只是原始目标值与MC目标值的最大化，可见式(3)
$$
\begin{aligned}
Q^{target}_{MCAC}(s_j^i,a_j^i)=max[Q^{target}(s_j^i,a_j^i),Q^{target}_{MC-\infty}(s_j^i,a_j^i)]
\end{aligned}\tag{3}
$$
最终，得到$Q$函数的损失函数为
$$
\begin{aligned}
J(\theta)=l(Q_{\theta}(s_j^i,a_j^i),Q^{target}_{MCAC}(s_j^i,a_j^i))
\end{aligned}\tag{4}
$$

MCAC算法效果

为了更好理解MCAC影响Q值估计的方法，基于SAC算法在Pointmass Navigation环境中训练50000步之后的Replay Buffer中$Q$值估计进行了可视化，可见图2所示。

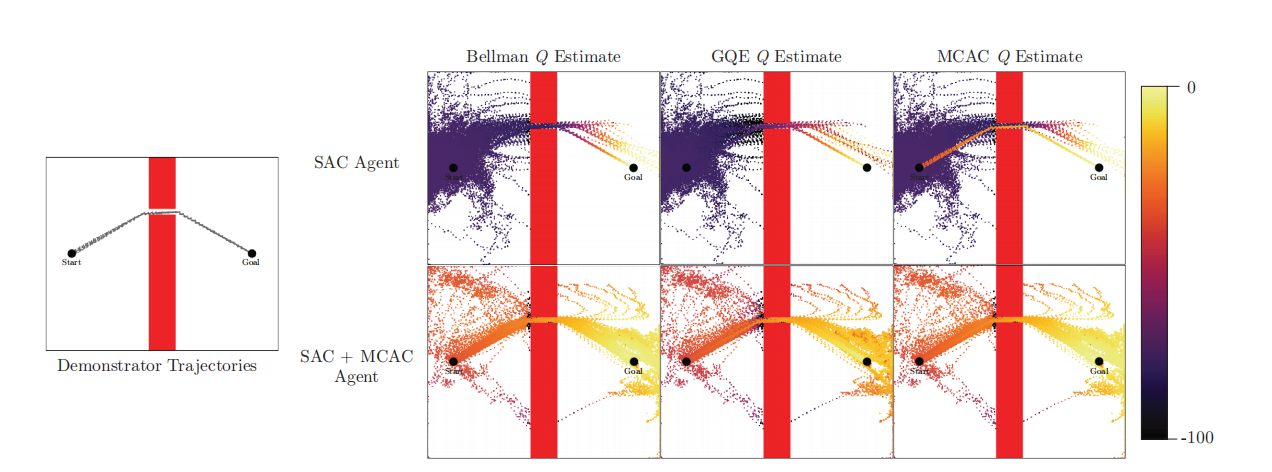
图2中Bellman Q Estimate是基于Bellman方程运算的Q值估计，也就是TD-Learning；GQE为利用GAE的方式计算Q值。

根据图2中上面一行，可知，无MCAC的SAC智能体无法学习到有用的$Q$函数，因此无法学习出完成任务的策略。同时，也可以看到GAE比Bellman的方式有效，但无MCAC有效。根据图2中下面一行，可知，若智能体利用了MCAC，那么可学习到有用的Q函数，从而可靠的完成任务，其Replay Buffer中Bellman估计、GAE估计以及MCAC估计相似。

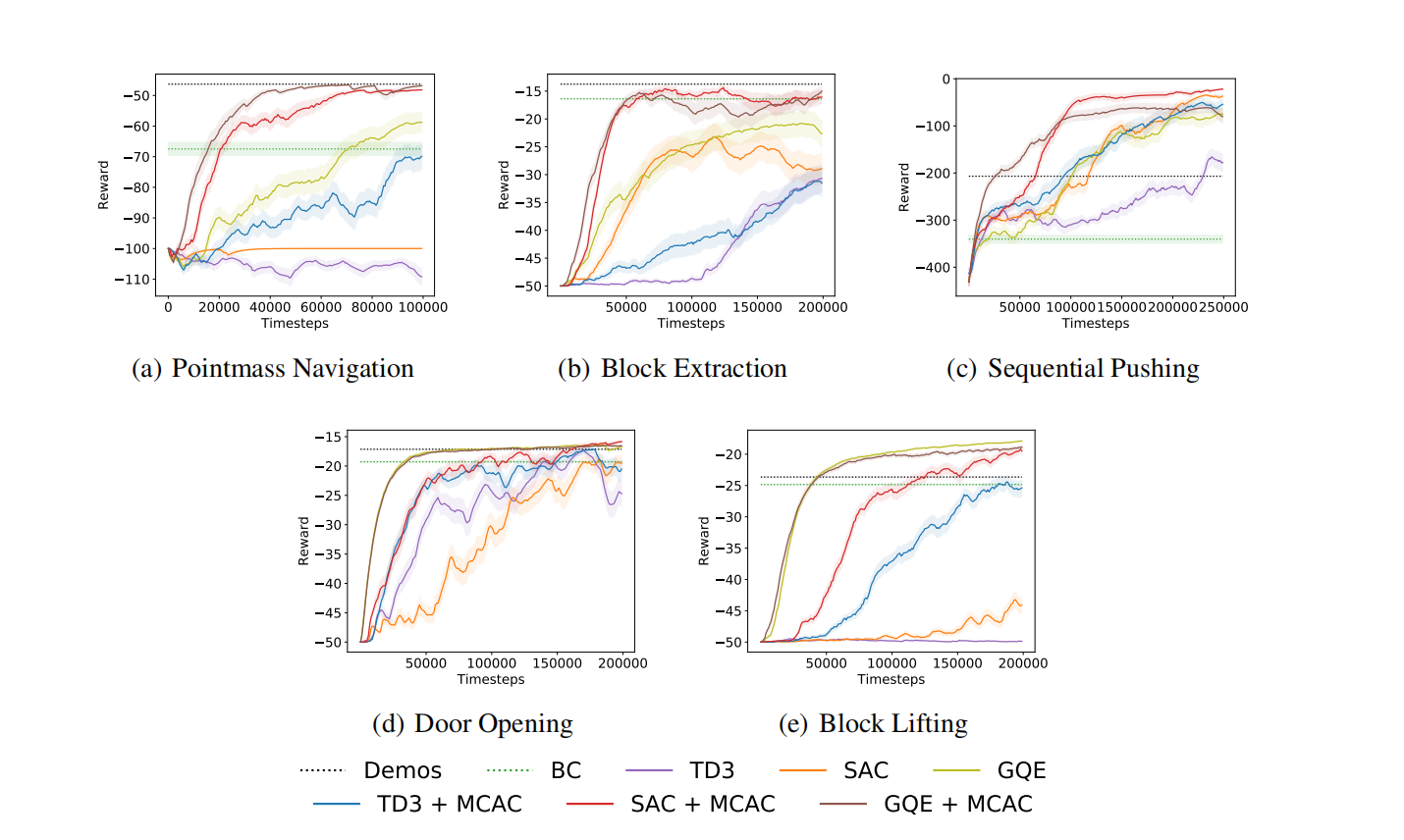
根据图3，可知，与SAC、TD3、以及GAE相比，MCAC增强的版本比原始版本算法性能优越，且样本效率高。

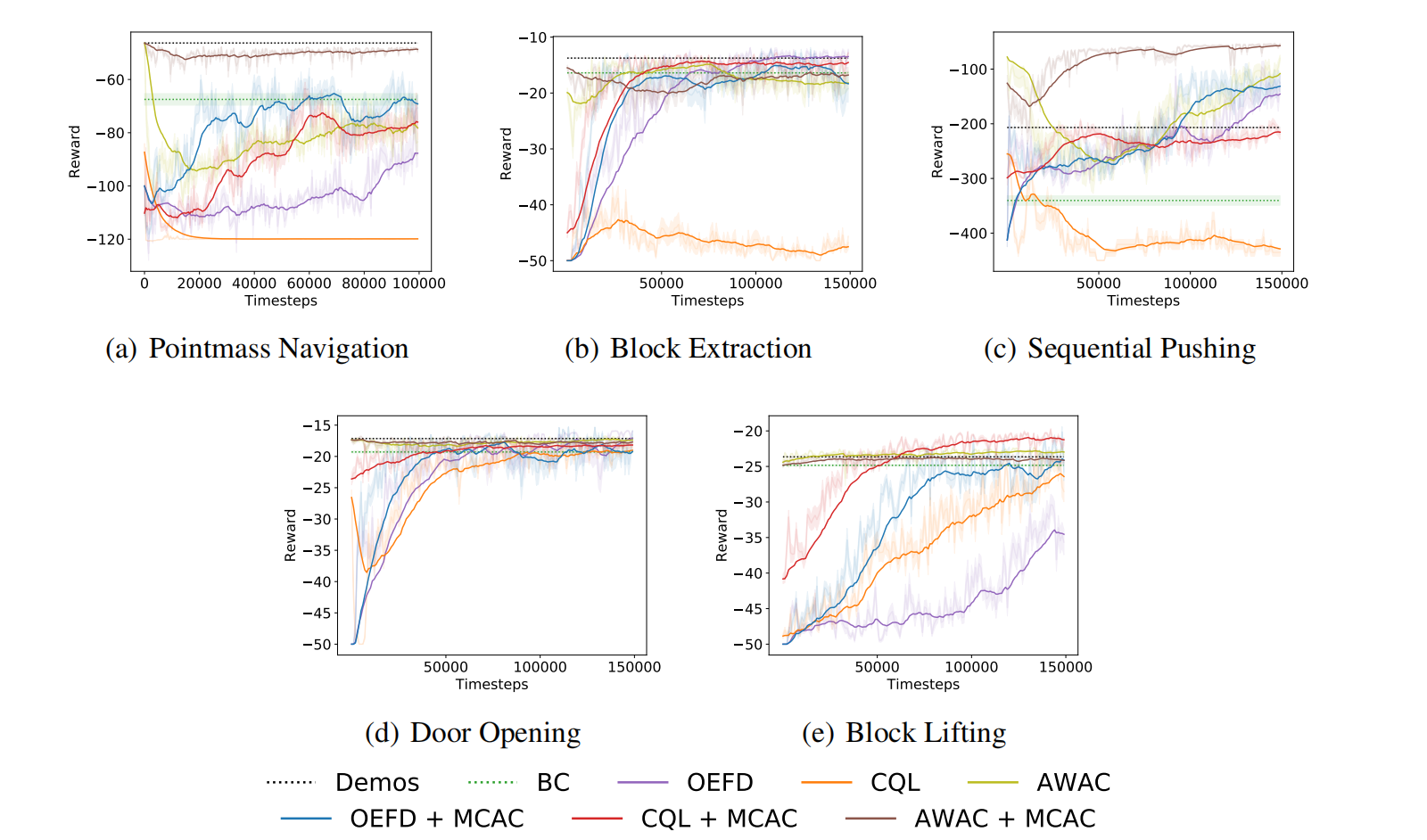
根据图4，可知，与Overcoming Exploration in Reinforcement Learning with Demonstrations、AWAC、以及CQL这类基于专家演示数据初始化策略的算法相比，MCAC增强的版本比原始版本算法性能优越，样本效率高，且训练更稳定。即使部分环境没有提升效果，但是也没有降低算法性能，即无负面影响。

实践经验

在利用MCAC增强SAC算法时，发现，会降低收敛速度且降低模型的性能。