IBC：隐式行为克隆

IBC(Implicit Behavior Cloning)在原理上很简单，就是把行为克隆视作基于能量建模的问题。在推理阶段执行通过采样或梯度下降寻找最优动作$\hat{\mathbf{a}}$的方式执行隐式回归，可见式(1)。
$$
\begin{aligned}
\hat{\mathbf{a}}=\underset{\mathbf{a}\in\mathcal{A}}{argmin}\quad E_{\theta}(\mathbf{o},\mathbf{a})
\end{aligned}\tag{1}
$$
实验结果表明，行为克隆由监督学习问题变为基于能量的建模问题，导致机器人完成任务性能得到提升：从双臂把小物品放进容器，到在1mm容忍度内精确推动bolcks，再到根据颜色分类物品，可见图1所示。IBC不仅能够建模多峰分布，还能够不连续函数。

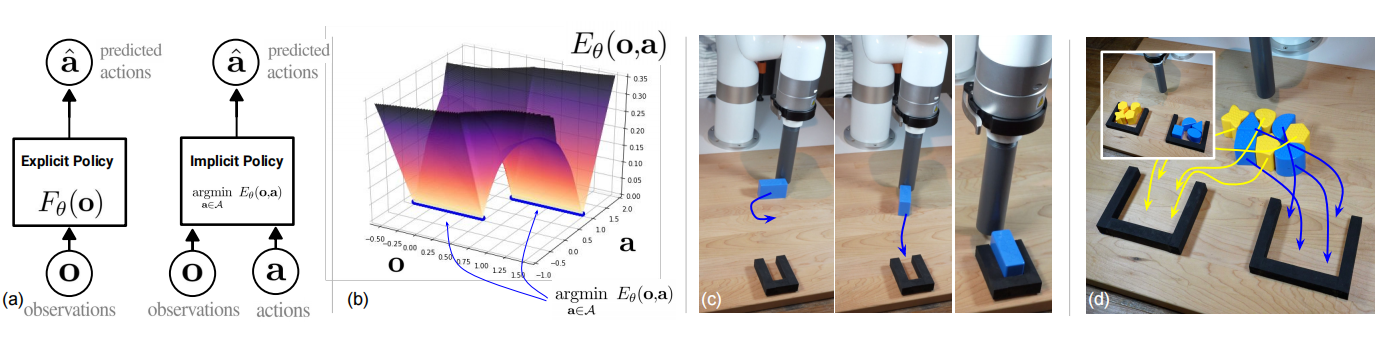
图1 (a)显式策略与隐式策略；(b)能量地图；(c)精确的块嵌入任务；(d)分类任务

隐式模型训练与推理

给定数据集$\{\mathbf{x}_i,\mathbf{y}_i\}$和回归界$\mathbf{y}_{min},\mathbf{y}_{max}\in\mathbb{R}^{m}$，模型训练由生成样本$\mathbf{x}_i$的负样本集合$\{\tilde{\mathbf{y}}_i^j\}_{j=1}^{N_{neg}}$，以及利用InfoNCE作为损失函数构成，可见式(2)所示。
$$
\begin{aligned}
\mathbf{\mathcal{L}}_{InfoNCE}=\sum_{i=1}^N -log(\tilde{p}_{\theta}(\mathbf{y}_i\vert\mathbf{x},\{\tilde{y}_i^j\}_{j=1}^{N_{neg}})) \\
\tilde{p}_{\theta}(\mathbf{y}_i\vert\mathbf{x},\{\tilde{y}_i^j\}_{j=1}^{N_{neg}})=\frac{e^{-E_{\theta}(\mathbf{x}_i,\mathbf{y}_i)}}{e^{-E_{\theta}(\mathbf{x}_i,\mathbf{y}_i)}+\sum_{j=1}^{N_{reg}}e^{-E_{\theta}(\mathbf{x}_i,\tilde{y}_i^j)}}
\end{aligned}\tag{2}
$$
其中，损失函数为$p_{\theta}(\mathbf{y}\vert\mathbf{x})$的负log似然。

能量模型训练之后，隐式推理能够通过随机优化的方式求解$\hat{\mathbf{y}}=argmin_{\mathbf{y}}E_{\theta}(\mathbf{x},\mathbf{y})$。IBC采用了三种训练方式，分别是：基于采样的方式、无倒数优化器的自回归变体、以及基于梯度的朗之万采样，更多的训练方法可见EBMs-Training。

相关思考

能量函数的输入为观测和动作，输出为"能量"，那么能量函数可看作观测与动作的匹配程度。若观测与动作越不匹配，那么能量越高；若观测与动作越匹配，那么能量越低。