Swish：搜索激活函数

深度神经网络是由线性变形和激活函数构成。其中，激活函数对深度神经网络的训练成功很重要。激活函数ReLU因其简单性和可靠性，而得到了广泛的采用。虽然许多实践者提出了ReLU的替代版，但是这些激活函数对于不同的模型和数据集往往拥有不一致的表现。由此，Searching for Activation Functions作者们利用自动搜索技术，找到了Swish激活函数，其性能不仅优越于ReLU，且表现一致。

Swish

Swish被定义为$x\cdot\sigma(\beta x)$，其中$\sigma(z)=(1+exp(-z))^{-1}$为sigmoid函数，$\beta$为常数或可训练参数。如图1所示，不同$\beta$值下的Swish函数。

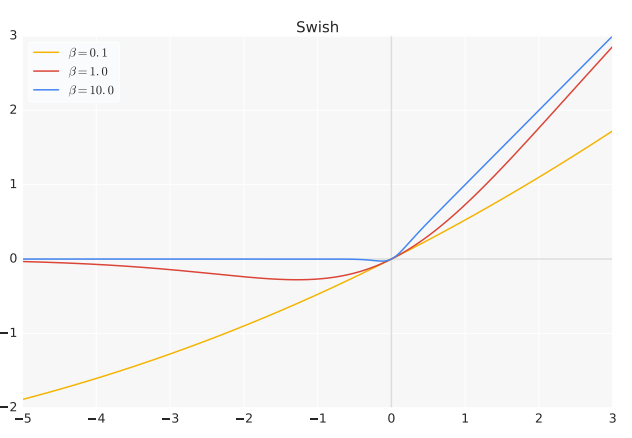
图1 Swish激活函数

若$\beta=1$，那么Swish等价于SiLU，提出于强化学习领域。若$\beta=0$，那么Swish函数变为线性函数$f(x)=\frac{x}{2}$。若$\beta\to\infty$，那么Swish函数类似于ReLU函数。因此，Swish函数可被视为线性函数与ReLU函数之间的非线性插值，由$\beta$控制的插值程度。

与ReLU一致，Swish无上界，有下界。与ReLU不一致，Swish为平滑和非单调的函数。实际上，大部分激活函数均无Swish函数的非单调性。Swish函数的一阶导数为
$$
\begin{aligned}
{f}'(x) &= \sigma(\beta x)+\beta x\cdot\sigma(\beta x)(1-\sigma(\beta x)) \\
&= \sigma(\beta(x))+\beta x\cdot\sigma(\beta x)-\beta x\cdot\sigma(\beta x)^2 \\
&= \beta x\cdot\sigma(x)+\sigma(\beta x)(1-\beta x\cdot\sigma(\beta x)) \\
&= \beta f(x)+\sigma(\beta x)(1-\beta f(x))
\end{aligned}\tag{1}
$$
如图5所示，不同$\beta$值下Swish函数的一阶导数。

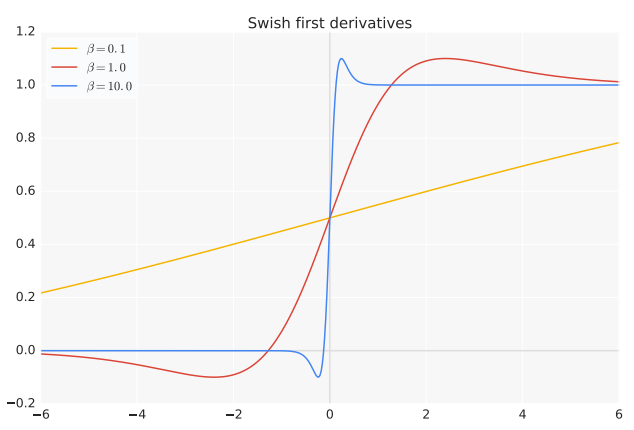
图2 Swish的一阶导数

$\beta$控制着一阶导数渐进于0与1的速度。若$\beta=1$，那么小于1.25的输入的导数小于1。同时，$\beta=1$的Swish有效性表示ReLU保护梯度的优势不再唯一。其中，保护梯度是指若$x\gt0$，那么导数为1。与ReLU相比，Swish的非单调性主要体现在$-5\le x\le0$区域，且非单调性的程度被$\beta$控制。若$\beta$为可训练参数，那么取值范围为$(0,1.5)$，且$\beta\approx 1$的数量最多。对于Swish网络，作者们还建议若利用BatchNorm，那么应设置缩放参数。同时，稍微降低学习率训练Swish网络。