GELU：高斯误差线性单元

在较早的阶段，人工神经单元利用二值阈值单元作为激活函数。后来，这些二值阈值被sigmoid函数代替，拥有了平滑性。然而，随着网络越来越深，利用sigmoid作为激活函数，反而不如ReLU这种非平滑且少概率的激活函数有效。同时，深度非线性分类器往往过拟合数据，所以网络设计者需要选择随机正则化器，例如：隐藏层添加随机噪音、droupout。最终，非线性激活函数与dropout共同决定神经元的输出。然而，两者仍然有明显的区别或独立，即彼此不包含。由此，GELU诞生了。如图1所示，GELU的激活效果。

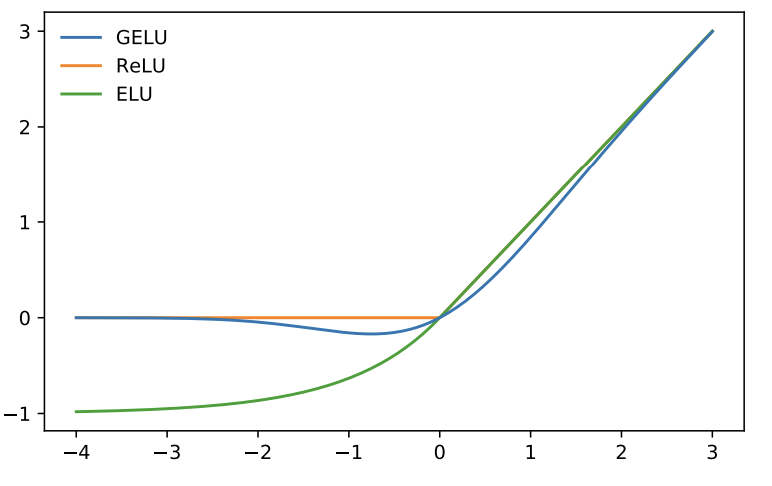
图1 GELU,ReLU,ELU

GELU的主要目的是结合dropout与ReLUs的特性。首先，ReLU使神经元产生一个确定的输出，即输入要么与0相乘，要么与1相乘。同时，dropout随机的乘以0。因此，作者们通过由输入随机决定的0-1掩码值融合这两个特性。确切的说，GELU为
$$
\begin{aligned}
GELU(x)=xP(X\le x)=x\Phi(x)=x\cdot\frac{1}{2}[1+erf(x/\sqrt{2})]
\end{aligned}\tag{1}
$$
式(1)中$X\sim\mathcal{N}(0,1)$且$erf(x)=\frac{2}{\sqrt{x}}\int_{0}^x e^{-t^2}dt$。之所以选择正态分布，是因为神经元的输入往往倾向于遵循正态分布，尤其利用了Batch Normalization技术。

GELU的近似为
$$
\begin{aligned}
&0.5x(1+tanh[\sqrt{2/\pi}(x+0.044715x^3)]) \\
&or\\
& x\sigma(1.702x)
\end{aligned}\tag{2}
$$
若利用Logistic分布的累积分布函数$\sigma(x)$，那么可得Sigmoid线性单元$SiLU(x)=x\sigma(x)$。