NeRF：利用神经辐射场作为场景表示用于视角合成

NeRF是一个利用全连接深度网络优化潜在连续体积场景函数的方法合成新视角的方法。该方法有两个步骤，分别是场景表示和体积渲染，可见图1所示。

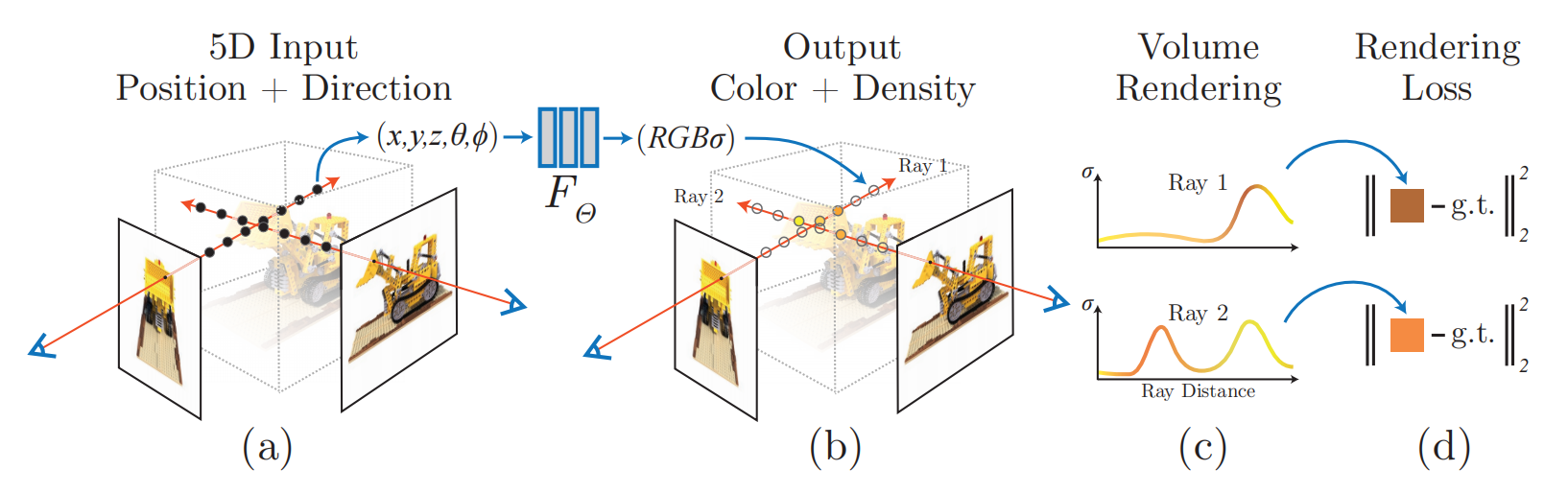
图1 NeRF概览与体积渲染概览

神经辐射场场景表示

作者们把场景表示为一个$5D$向量值的函数，输入为$3D$坐标$\mathbf{x}=(x,y,z)$和2D视角方向$(\theta,\phi)$，输出为发出的颜色$\mathbf{c}=(r,g,b)$和体积密度$\sigma$。对于视角方向，利用3D笛卡尔单位向量$d$表示。在实践中，利用MLP作为函数拟合器为$F_{\Theta}:(\mathbf{x},\mathbf{d}\to(\mathbf{c},\sigma))$

为了鼓励表示的多视角一致性，只利用位置$\mathbf{x}$预测体积密度，利用位置和视角方向预测RGB颜色$\mathbf{c}$。确切的说，利用8层全连接神经网络以3D坐标为输入，输出密度$\sigma$和256维的特征向量。接下来，再利用特征向量和视角方向作为一个全连接层网络的输入，输出视角依赖的RGB颜色。

利用辐射场进行体积渲染

作者们利用经典的体积渲染原则渲染场景内任何射线的颜色。体积密度$\sigma(\mathbf{x})$可被解释为射线终止在位置$\mathbf{x}$处的可微分概率。那么，相机射线$\mathbf{r}(t)=\mathbf{o}+t\mathbf{d}$在$t_n$与$t_f$之间被期望的颜色$C(\mathbf{r})$为
$$
\begin{aligned}
C(\mathbf{r})=\int_{t_n}^{t_f}T(t)\sigma(\mathbf{r}(t))\mathbf{c}(\mathbf{r}(t),d)dt,\quad where\quad T(t)=exp(-\int_{t_n}^t\sigma(\mathbf{r}(s))ds)
\end{aligned}\tag{1}
$$
函数$T(t)$表示的是沿着射线从$t_n$至$t$的累积透明度，即射线$t_n$到$t$的穿透概率。

为了提高渲染的分辨率，作者们利用积分法估计连续积分函数$C(\mathbf{r})$。确切的说，积分区间$[t_n,t_f]$被均匀的分为$n$份，然后从每个bin中随机均匀的采样
$$
\begin{aligned}
t_i\sim\mathcal{U}[t_n+\frac{i-1}{N}(t_f-t_n),t_n+\frac{i}{N}(t_f-t_n)]
\end{aligned}\tag{2}
$$
然后，根据这些样本，利用积分规则估计$C(\mathbf{r})$
$$
\begin{aligned}
\hat{C}(\mathbf{r})=\sum_{i=1}^NT_i(1-exp(-\sigma_i\delta_i))\mathbf{c}_i,\quad where\quad T_i=exp(-\sum_{j=1}^{i-1}\sigma_j\delta_j)
\end{aligned}\tag{3}
$$

神经辐射场的优化

NeRF的两个重要模块：神经辐射场与体积渲染，已经被详细的介绍了。接下来，为了提高MLP表示高频函数，引入了输入坐标的位置编码。同时，利用分层采样提高采样效率。

位置编码

尽管神经网络属于通用函数拟合器，但是作者们发现神经网络直接以坐标为输入往往导致在高频变化区域的表示性能较差，这与深度神经网络倾向于学习低频函数的发现一致。由此，作者们把输入经过傅立叶变化形成编码，再输入到神经网络，从而使网络学习到高频函数
$$
\begin{aligned}
\gamma(p)=(sin(2^{0}\pi p),cos(2^0\pi p),\cdots,sin(2^{L-1}\pi p),cos(2^{L-1}\pi p))
\end{aligned}\tag{4}
$$
函数$\gamma$独立的分别应用在三维坐标$\mathbf{x}$的每个元素和笛卡尔视角方向单位向量$\mathbf{d}$中每个元素，每个向量均被归一化。对于$\gamma(\mathbf{x})$设置$L=10$，对于$\gamma(\mathbf{d})$设置$L=4$。

分层体积渲染

由于自由区域和封闭区域对渲染图片没有贡献，导致稠密的渲染策略不高效。因此，作者们提出了分层表示，从而根据最终渲染的期望效果成比例的分配样本。

确切的说，作者们同时优化两个网络，分别是"coarse"和"fine"。首先，利用分层采样法采样$N_c$个位置，利用式(2)和式(3)进行估计。然后，根据"coarse"网络的输出，沿着每个射线产生更合理的样本点。为了实现该功能，作者们先把"coarse"网络的式(3)变为
$$
\begin{aligned}
\hat{C}_{c}(\mathbf{r})=\sum_{i=1}^{N_c}w_ic_i,\quad w_i=T_i(1-exp(-\sigma_i\delta_i))
\end{aligned}\tag{5}
$$
正则化权重为$\hat{w}_i=w_i/\sum_{j=1}^{N_c}w_j$产生一个沿着射线分片常量的概率密度函数。接下来，根据该概率密度函数利用逆变换采样法，采样出$N_f$个位置。最后，利用"fine"网络对$N_c+N_f$个点进行估计。这种方式会对被期望包含可见内容的区域收集更多样本。

实现细节

对于每个场景，神经连续体积表示网络只需要捕获的场景RGB图片、相机位姿和内参、以及场景界限。在每个优化步骤，从数据集中所有像素集合中随机采样一个batch的相机射线，然后基于层级分层采样方法估计像素，损失函数为
$$
\begin{aligned}
\mathcal{L}=\sum_{\mathbf{r}\in\mathcal{R}}[\Vert\hat{C}_{\mathcal{c}}(\mathbf{r})-C(\mathbf{r})\Vert_2^2+\Vert\hat{C}_{f}(\mathbf{r})-C(\mathbf{r})\Vert_2^2]
\end{aligned}\tag{6}
$$
其中，$\mathcal{R}$为每个batch中射线集合，$C(\mathbf{r}),\hat{C}_c(\mathbf{r}),\hat{C}_{f}(\mathbf{r})$分别是真实值、coarse体积预测、以及fine体积预测的RGB颜色。

相关思考

NeRF实现了SOTA结果，这表明神经辐射场可以作为很强的场景3D表示。这种表示也可用在操作任务以表示3D场景，相关工作可见NeRF in the Palm of Your Hand: Corrective Augmentation for Robotics via Novel-View Synthesis。