生成式建模的流匹配

扩散模型的性能虽优越，但是其限制了采样概率路径的空间。同时，扩散模型不仅拥有较长的训练时间，还需要通过蒸馏等方法提高采样效率。与之相比，连续正则化流CNFs能够建模任意的概率路径，但受限于无可扩展的CNF训练算法。为了解决CNFs模型训练的不稳定性，流匹配FM是一个基于回归固定条件概率路径向量场的Simulation-Free训练方法，为CNFs模型训练提供了等效梯度。该方法不仅拥有较好的样本质量，且训练与推理效率得到了很大的提升。

Plus：根据笔者的理解Simulation-Free属于一步生成的方式，即不需要像扩散模型的前向添加噪音和逆向移除噪音的过程。

连续正则化流

数据点$x=(x^1,\ldots,x^d)\in\mathbb{R}^d$的数据空间为$\mathbb{R}^d$。概率密度路径可被定义为$p:[0,1]\times\mathbb{R}^d\rightarrow\mathbb{R}_{\gt0}$，其为随时间变化的概率密度函数，即$\int p_t(x)dx=1$。若随时间变化的向量场为$v:[0,1]\times\mathbb{R}^d\rightarrow\mathbb{R}^d$，那么随时间变化的微分图或流$\phi:[0,1]\times\mathbb{R}^d\rightarrow\mathbb{R}^d$可通过常微分方程ODE定义为
$$
\begin{aligned}
\frac{d}{dt}\phi_t(x)&=v_t(\phi_t(x)) \\
\phi_0(x)&=x
\end{aligned}\tag{1}
$$
CNFs作者们表明利用神经网络建模向量场$v_t(x;\theta)$，从而可得到流$\phi_t$的深度参数模型，即连续正则化流。一个正则化流可通过前推方程把简单的先验分布$p_0$变为复杂的分布$p_1$。其中，前推方程为
$$
\begin{aligned}
p_t=[\phi_t]* p_0
\end{aligned}\tag{2}
$$
式(2)前推运算符$*$为
$$
\begin{aligned}
~[\phi_t]*p_0(x)=p_0(\phi^{-1}_t(x))det[\frac{\partial\phi^{-1}_t}{\partial x}(x)]
\end{aligned}\tag{3}
$$
若流$\phi_t$满足式(3)，那么向量场$v_t$可用于生成概率密度路径$p_t$。对于一个向量场，可利用连续性方程测试其是否可以生成一个概率路径。其中，连续性方程为
$$
\begin{aligned}
\frac{d}{dt}p_t(x)+div(p_t(x)v_t(x)) = 0
\end{aligned}\tag{26}
$$
式(26)中$div=\sum_{i=1}^d\frac{\partial}{\partial x^i}$为divergence运算。

流匹配

一个随机变量为$x_1$的未知数据分布为$q(x_1)$，即只能从分布$q(x_1)$中获取样本，而不知道密度函数本身。此外，$p_t$表示一个概率路径，$p_0=p$为一个简单的分布，例如：标准正态分布$p(x)=\mathcal{N}(x\vert 0,I)$，且$p_1$近似等于分布$q$。由此，流匹配的目标函数是匹配目标概率路径，即 从$p_0$流向$p_1$。

给定目标概率密度路径$p_t(x)$与对应的向量场$u_t(x)$，那么流匹配的目标函数为
$$
\begin{aligned}
\mathcal{L}_{FM}(\theta)=\mathbb{E}_{t,p_t(x)}\Vert v_t(x)-u_t(x)\Vert^2
\end{aligned}\tag{4}
$$
式(4)中$t\sim \mathcal{U}[0,1]$

从形式上看，流匹配是一个简单的目标函数，但是由于对合适的$p_t$和$u_t$先验不知而导致问题很难求解。即使存在很多满足$p_1(x)\approx q(x)$的概率路径，也因无法得到生成$p_t$的封闭形式$u_t$而不可行。

基于条件概率路径与向量场构建$p_t,u_t$

构建目标概率路径的简单方式是通过一个混合的简单概率路径：给定一个数据样本$x_1$，$p_t(x\vert x_1)$为条件概率路径，其在时刻$t=0$满足$p_0(x\vert x_1)=p(x)$。那么，可在时刻$t=1$设计$p_1(x\vert x_1)$为在$x=x_1$周围，例如：$p_1(x\vert x_1)=\mathcal{N}(x\vert x_1,\sigma^2 I)$，一个以$x_1$为均值和标准差$\sigma\gt0$足够小的正态分布。关于$q(x_1)$求条件概率路径可得边际概率路径
$$
\begin{aligned}
p_t(x)=\int p_t(x\vert x_1)q(x_1)dx_1
\end{aligned}\tag{5}
$$
特别的，在$t=1$时刻，边际概率$p_1$属于数据分布$q$的近似
$$
\begin{aligned}
p_1(x)=\int p_1(x\vert x_1)q(x_1)dx_1\approx q(x)
\end{aligned}\tag{6}
$$
有趣的是，可定义边际向量场为
$$
\begin{aligned}
u_t(x)=\int u_t(x\vert x_1)\frac{p_t(x\vert x_1)q(x_1)}{p_t(x)}dx_1
\end{aligned}\tag{7}
$$
式(7)中$u_t(\cdot\vert x_1):\mathbb{R}^d\rightarrow\mathbb{R}^d$是一个生成$p_t(\cdot\vert x_1)$的条件向量场。这种聚合条件向量场实际上生成了建模边际概率路径的向量场。

Plus: 笔者认为$\frac{p_t(x\vert x_1)q(x_1)}{p_t(x)}=p(x_1\vert x)$。总感觉可以替换为$q(x_1)$，那就变得很简单了。之所以没有这样做，或许是为了强调条件吧。若把$p_t(x)$视为归一化项，那么可以理解为以$x,x_1$同时出现的概率作为权重，对条件向量场进行加权平均。

由此，在条件向量场和边际向量场之间构建了链接，从而可允许把不可知且不可行的边际向量场分解成简单的条件向量场，而条件向量场只取决于单个数据样本。

在论文中，作者们不仅进行了证明还给出了形式化定义。同时，该理论也可根据扩散混合表示理论推导。

条件流匹配

由于式(5)和式(7)中边际概率路径和向量场的定义计算积分，因此计算$u_t$也是很困难的，即很难计算一个原始流匹配目标函数的无偏估计器。由此，作者们提出了条件流匹配目标函数
$$
\begin{aligned}
\mathcal{L}_{CFM}(\theta)=\mathbb{E}_{t,q(x_1),p_x(x\vert x_1)}\Vert v_t(x)-u_t(x\vert x_1)\Vert^2
\end{aligned}\tag{8}
$$
式(8)中$t\sim\mathcal{U}[0,1],x_1\sim q(x_1),x\sim p_t(x\vert x_1)$

与流匹配目标函数不同，条件流匹配目标函数很容易采样出一个无偏估计，只要可从$p_t(x\vert x_1)$中高效的采样和高效的计算$u_t(x\vert x_1)$，而这两项是在每个样本基础上定义的。作者们也观测到优化条件流匹配目标函数等同于优化流匹配目标函数。因此，只需要设计合适的条件概率路径和向量场，就可以训练生成边际概率路径$p_t$的CNF。

条件概率路径与向量场

条件流匹配目标函数可与条件概率路径和条件向量场的任何选择结合。作者们讨论了高斯条件概率路径中$p_t(x\vert x_1)$和$u_t(x\vert x_1)$的构建。确切的，条件概率路径为
$$
\begin{aligned}
p_t(x\vert x_1)=\mathcal{N}(x\vert \mu_t(x_1),\sigma_t(x_1)^2I)
\end{aligned}\tag{9}
$$
其中，$\mu:[0,1]\times\mathbb{R}^d\rightarrow\mathbb{R}^d$为高斯分布的依赖于时间的均值，$\sigma:[0,1]\times\mathbb{R}\rightarrow\mathbb{R}_{\gt0}$为依赖于时间的标量标准差。$\mu_{0}(x_1)=0,\sigma_0(x_1)=1$从而所有条件概率路径都拟合到相同标准高斯分布$p_{0}(x)=p(x)=\mathcal{N}(x\vert 0,I)$。$\mu_1(x_1)=x_1,\sigma_1(x_1)=\sigma_{min}$设置的足够小以至于$p_1(x\vert x_1)$为以$x_1$为中心的高斯分布。

有无穷的向量场可生成特别的概率路径。然而，大量的向量场因使潜在分布不变的元件的存在而产生不必要的计算，所以作者们利用最简单的向量场。该向量场与高斯分布的正则化变形相对应，其流为
$$
\begin{aligned}
\psi_t(x)=\sigma_t(x_1)x+\mu_t(x_1)
\end{aligned}\tag{10}
$$
式(10)中$x$为标准高斯分布，$\psi_t(x)$仿射变换。可以理解为，按照式(3)$\psi_t$从噪音分布$p_0(x\vert x_1)=p(x)$流向$p_t(x\vert x_1)$，即
$$
\begin{aligned}
~[\psi_t]*p(x)=p_t(x\vert x_1)
\end{aligned}\tag{11}
$$
该流的生成条件概率路径的向量场为
$$
\begin{aligned}
\frac{d}{dt}\psi_t(x)=u_t(\psi_t(x)\vert x_1)
\end{aligned}\tag{12}
$$
那么，以$x_0$为输入，CFM损失为
$$
\begin{aligned}
\mathcal{L}_{CFM}(\theta)=\mathbb{E}_{t,q(x_1),p(x_0)}\Vert v_t(\psi_t(x_0))-\frac{d}{dt}\psi_t(x_0)\Vert
\end{aligned}\tag{13}
$$
由于$\psi_t$为简单的仿射映射，因此可利用式(12)求解$u_t$的封闭形式。

最后，作者们还讨论了概率流的两个特例，分别是扩散模型和Wasserstein-2最优传输解决方案。同时，发现，条件最优传输(Optimal Transport,OT)路径比扩散路径还简单，OT形成了直线轨迹而扩散路径为曲线，可见图1所示。

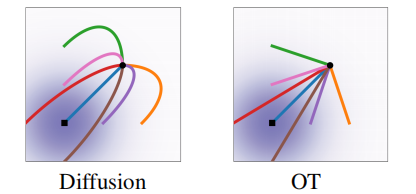
图1 扩散与OT轨迹