哪种训练方法导致GANs真实的拟合 (二)?
在上一篇哪种训练方法导致GANs真实的拟合(一)?中,表示了对于低维流形数据,GAN的训练往往无法拟合到Nash均衡点,这是训练不稳定性造成的。接下来,这篇文章将分析不稳定性的来源,且提出降低不稳定性的方法。
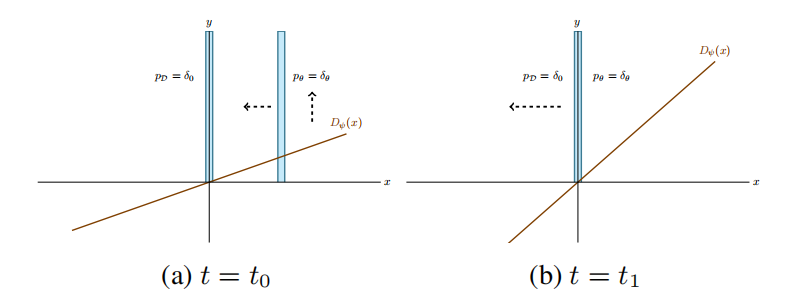
图1 基于梯度下降的GAN优化永远无法拟合的反例可视化
不稳定性的来源
作者们给出了上篇文章中图1显示的振荡行为的解释:在生成器远离真实数据分布时,判别器推动生成器朝向真实数据分布移动。同时,判别器变得更加确定,提高了判别器的斜率。此时,若判别器接近目标分布,判别器的斜率是最大的,推动生成器远离目标分布。因此,生成器再次远离真实数据分布,而判别器会由正到负改变斜率。一段时间后,以与训练开始相似的情况结束。这种过程会确定的重复,且永远不会拟合。
另一种解释方式是:考虑训练算法在Nash均衡的局部行为。在Nash均衡的附近,没有什么可推动判别器向零斜率前进。即使生成器精确的初始化为目标分布,这里也不存在动机推动判别器移向均衡点。因此,在均衡点的训练是不稳定的。
判别器梯度正交于数据分布的现象,也可产生于更复杂的样本:只要数据分布为低维流形,判别器的类别足够大,那么判别器就没有足够动机产生正交于数据流形正切空间的零梯度,从而拟合均衡判别器。在这种情况下,判别器无法为生成器正交于数据分布提供有用的梯度,从而生成器也无法拟合。
正则化策略
正如前面讨论的,非正则化GAN训练无法拟合到Nash均衡。接下来,作者们讨论了一些影响Dirac-GAN拟合的正则化技术。同时,作者们也发现了GAN原始论文中提出的非饱和损失可导致连续系统拟合,但其拟合速率很慢。
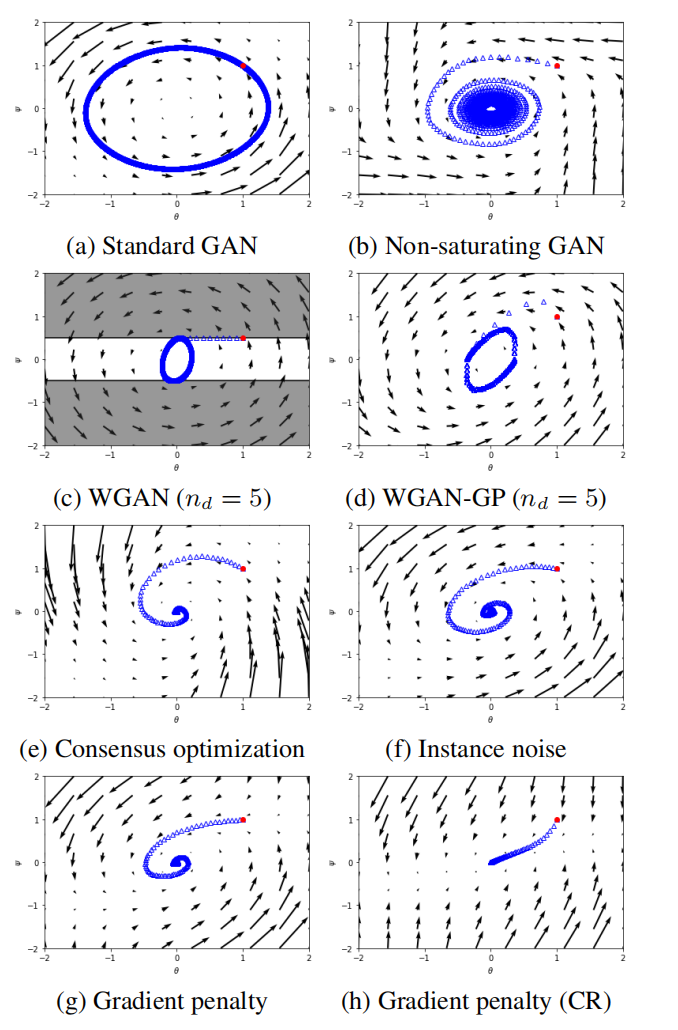
图3 不同训练方法的GAN拟合特性
Wasserstein GAN
GAN可被解释为最小化真实数据分布与生成器分布之间概率发散程度或距离。这种发散或距离是通过考虑判别器的最好响应策略得到的,最终导致目标函数只包含生成器参数。这种距离对生成器参数可能是不连续的,也可能在数据分布与生成器分布不匹配时取无穷值。根据这一观测,产生了许多GANs的正则化技术。
为了使这种距离关于生成器参数连续,WGANs作者们利用Wasserstein-divergence替换JS-divergence。在WGANs中,作者们利用$f(t)=t$,且限制判别器类别为常数$g_0\gt0$的Lipschitz连续约束。虽然理论上只要判别器一直被训练直到拟合则WGANs会拟合,但是实践中WGANs的生成器每次更新只对应判别器的有限次数更新。然而,在Nash均衡附近,最优判别器参数为当前生成器参数的不连续函数:对于Dirac-GAN,最优判别器参数在$\theta$符号发生改变时,由$\psi=-1$变为$\psi=1$。随着在均衡点附近梯度变小,梯度更新不会导致判别器拟合。最的来说,训练动力学再次被梯度向量场的雅可比所决定:
引理3.1. 一个利用同步梯度下降或交替梯度下降更新的WGAN,对于Dirac-GAN通常不会拟合到Nash均衡点。其中,生成器的每次更新都对应固定次数的判别器更新,学习率固定为$h\gt0$。
如图3c所示,WGANs的训练行为。这种训练是建立在每次生成器更新对应固定次数的判别器更新。或许,更仔细的训练可确保判别器精确的保持最优,或两倍规模的训练可能会确保WGANs拟合。
Instance noise
稳定化GANs的常用技术是添加实例噪音,即对于数据点添加独立的高斯噪音。虽然原始的动机是使数据与生成分布之间的概率距离可被很好的定义,但是仍不清楚实例噪音对训练算法本身和寻找Nash均衡能力的效果。然而,论文Gradient descent GAN optimization is locally stable表明在绝对连续分布情况下,在合适的假设下,梯度下降优化的GAN可局部拟合。
对于Dirac-GAN来说,可有:
引理3.2. 若高斯实例噪音的标准差为$\sigma$,梯度向量场的雅可比的特征值为
$$
\begin{aligned}
\lambda_{1/2}={f}''(0)\sigma^2\pm\sqrt{{f}''(0)^2\sigma^4-{f}'(0)^2}
\end{aligned}
$$
特别的,若${f}''\lt0$且$\sigma\gt0$,那么特征值均有负实数部分。因此,同步梯度和交替梯度更新在足够小的学习率下GANs会局部拟合。
有趣的是,引理3.2.中存在一个关键噪音级别$\sigma^2_{critical}=\vert{f}'(0)\vert/\vert{f}''(0)\vert$。若噪音级别小于关键噪音级别,那么在均衡点附近雅可比的特征值有非零的虚数部分。其中,虚数部分会使GANs优化在均衡点附近的梯度向量场拥有一个旋转部分。若噪音级别大于关键噪音级别,那么所有雅可比的特征值均为实数。若$\sigma=\sigma_{critical}$,那么优化问题属于最好的行为:在这种情况下,对于$h=\vert{f}'(0)\vert^{-1}$可实现二次拟合。如图4b所示,实例噪音对特征值的效果,其表明了随着$\sigma$从$0$到$2\sigma_{critical}$时两个特征值的迹。
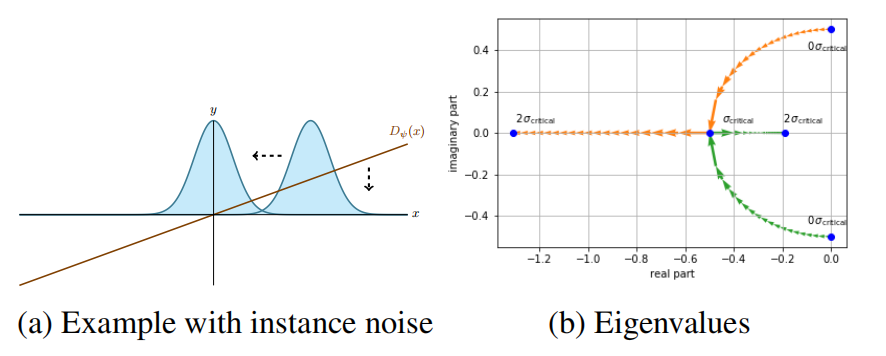
图4 带有实例噪音的Dirac-GAN
图3f为带有实例噪音的GAN的训练行为,表明实例噪音确实在梯度向量场创建了一个强的径向元件,从而使训练算法拟合。
Zero-centered gradient penalties
论文Stabilizing Training of Generative Adversarial Networks through Regularization推导出实例噪音的局部近似,产生了判别器的零为中心的梯度惩罚。
对于Dirac-GAN,判别器梯度的二范数惩罚为
$$
\begin{aligned}
R(\psi)=\frac{\gamma}{2}{\psi}^2
\end{aligned}
$$
引理3.3. 基于梯度正则化的Dirac-GAN的梯度向量场的雅可比在均衡点的特征值为
$$
\begin{aligned}
\lambda_{1/2}=-\frac{\gamma}{2}\pm\sqrt{\frac{{\gamma}^2}{4}-{f}'(0)^2}
\end{aligned}
$$
对于$\gamma\gt0$,所有特征值均有负实数部分。因此,同步或交替梯度下降均会导致Dirac-GAN以足够小的学习率局部拟合。
正如实例噪音,这里也存在一个关键正则化参数$\gamma_{critical}=2\vert{f}'(0)\vert$,会产生局部无旋转的向量场。如图3g所示,带有梯度惩罚的Dirac-GAN的训练行为可视化。如图3h所示,带有梯度惩罚和关键正则化参数的GAN的训练行为。根据3h可知,在Nash均衡向量场附近不存在一个旋转部分,因此行为与标准优化问题相似。
一般GANs的拟合特性
简化梯度惩罚
论文Stabilizing Training of Generative Adversarial Networks through Regularization中提出的零为中心的梯度惩罚主要用于惩罚判别器偏离于Nash均衡。实现该方法的最简单方式是只惩罚真实数据的梯度:在生成器产生真实数据分布且判别器在数据流形上输出为0的情况下,梯度惩罚用于确保判别器不能创建正交于数据流形的非零梯度。那么,正则化项为
$$
\begin{aligned}
R_1(\psi):=\frac{\gamma}{2}E_{p_{\mathcal{D}}(x)}[\Vert\nabla D_{\psi}(x)\Vert^2]
\end{aligned}
$$
plus:这里的是确保不存在正交于数据流形的非零梯度,与前面的径向非零梯度导致收敛不一致。
同时,作者们也考虑相似的正则化项,用于惩罚在当前生成器分布上的判别器梯度
$$
\begin{aligned}
R_2(\theta,\psi):=\frac{\gamma}{2}E_{p_{\theta}(x)}[\Vert\nabla D_{\psi}(x)\Vert^2]
\end{aligned}
$$
最终,作者们证明了基于梯度惩罚的GAN训练可以线性速率拟合。
引用方法
请参考:
li,wanye. "哪种训练方法导致GANs真实的拟合 (二)?". wyli'Blog (Oct 2024). https://www.robotech.ink/index.php/archives/643.html
或BibTex方式引用:
@online{eaiStar-643,
title={哪种训练方法导致GANs真实的拟合 (二)?},
author={li,wanye},
year={2024},
month={Oct},
url="https://www.robotech.ink/index.php/archives/643.html"
}