哪种训练方法导致GANs真实的拟合 (一)?
GANs属于强有力的隐变量模型,可以用于学习复杂的真实世界数据的分布。然而,实践中发现,GANs很难训练,且观测到基于梯度下降方法的GAN优化无法拟合。因此,研究人员对GANs的训练,提出了更好的训练算法。同时,这些算法拥有更好的理论理解。尽管如此,对于GANs的训练动力学仍没有完全理解。由此,论文Which Training Methods for GANs do actually Converge?作者们进行了如下研究:
- 确定了一个简单且典型的反例,表明基于梯度下降的GAN优化不总是局部拟合。
- 讨论了之前提出的正则化技术是否可以稳定化训练,以及如何稳定化训练。
- 引入了一个简单的梯度惩罚且证明了正则化的GAN训练动力学,可实现局部拟合。
与之前通过检测相关梯度向量场的雅可比特征值的方式分析训练动力学的方式不同,作者们通过考虑简单且典型的例子分析GANs训练动力学。
训练的不稳定性
背景知识
GANs被定义为两个玩家(判别器与生成器)的min-max博弈。其中,判别器尝试区分真实数据与生成数据,而生成器生成数据迷惑判别器。原论文中作者表明:若生成器和判别器有足够能力近似任意实数值函数,那么两个玩家之间的Nash均衡可被生成器和判别器实现。
根据Gradient descent GAN optimization is locally stable表示,两个玩家之间的训练目标函数可被表述为
$$
\begin{aligned}
L(\theta,\psi)=E_{p(z)}[f(D_{\psi}(G_{\theta}(z)))]+E_{p_{\mathcal{D}}(x)}[f(-D_{\psi}(x))]
\end{aligned}
$$
函数$f$的常见选择为$f(t)=-log(1+exp(-t))$,从而产生与原始GAN论文一致的损失函数。
在这里,作者们假设$f$属于连续可微的,且对于$\forall t\in\mathbb{R}$有${f}'(t)\neq0$
确切的说,生成器的目标是最小化损失函数,而判别器的目标是最大化损失函数。为了寻找到Nash均衡点$(\theta^{*},\psi^{*})$,通过可同步梯度下降SimGD或交替梯度下降AltGD训练两个神经网络。在论文The Numerics of GANs中,该两个梯度下降算法被描述为固定点算法,即对生成器参数值$\theta$和判别器参数值$\psi$分别执行运算$F_h(\theta,\psi)$。例如:同步梯度下降对应于运算$F_h(\theta,\psi)=(\theta,\psi)+hv(\theta,\psi)$,且$v(\theta,\psi)$表示梯度向量场
$$
\begin{aligned}
v(\theta,\psi):=\begin{pmatrix}
-\nabla_{\theta}L(\theta,\psi) \\
\nabla_{\psi}L(\theta,\psi)
\end{pmatrix}
\end{aligned}
$$
类似的,交替梯度下降被描述为运算$F_h=F_{2,h}\circ F_{1,h}$,且$F_{1,h}$和$F_{2,h}$分别为生成器和判别器执行的更新。
在论文The Numerics of GANs中,表明GAN训练的局部拟合可通过均衡点的雅可比${F}'_h({\theta}^{*},{\psi}^{*})$场进行分析:
- 若${F}'_h({\theta}^{*},{\psi}^{*})$拥有绝对值大于$1$的特征值,那么训练算法通常不会拟合到$({\theta}^{*},{\psi}^{*})$。
- 若所有特征值的绝对值小于1,那么训练将以线性速率$\mathcal{O}(\vert\lambda_{max}\vert^k)$拟合到$({\theta}^{*},\psi^{*})$。其中,$\lambda_{max}$为均值最大的特征值。
- 若所有特征值均在一个单位球上,那么算法可能拟合、发散、或两者都不。若拟合,那么拟合速率通常为次线性率。
论文Gradient descent GAN optimization is locally stable在连续系统中,展示相似的结果:
- 若静态点$({\theta}^{*},\psi^{*})$处雅可比${v}'({\theta^{*},\psi^{*}})$所有特征值均有负实数部分,那么连续系统以线性速率局部拟合。
- 若静态点$({\theta}^{*},\psi^{*})$处雅可比${v}'({\theta^{*},\psi^{*}})$所有特征值均有正实数部分,那么连续系统均不局部拟合。
- 若静态点$({\theta}^{*},\psi^{*})$处雅可比${v}'({\theta^{*},\psi^{*}})$所有特征值均有零实数部分,那么连续系统可能拟合、发散、或两者均不。若拟合,则会以次线性速率拟合。
其中,连续系统是指
$$
\begin{aligned}
\begin{pmatrix}
\dot{\theta}(t) \\
\dot{\psi}(t)
\end{pmatrix}=\begin{pmatrix}
-\nabla_{\theta}L(\theta,\psi) \\
\nabla_{\psi}L(\theta,\psi)
\end{pmatrix}
\end{aligned}
$$
Dirac-GAN
Simple experiments, simple theorems are the building blocks that help us understand more complicated systems.
Ali Rahimi - Test of Time Award speech, NIPS 2017
接下来,作者们描述一个简单且典型的反例,以表示在通常情况下无正则化的GAN训练既不会局部也不会全局拟合。
定义2.1. Dirac-GAN由一个不变的生成器分布$p_{\theta}=\delta_{\theta}$和一个线性判别器$D_{\psi}(x)=\psi\cdot x$构成。真实数据分布$p_{\mathcal{D}}$由以0为中心的Dirac分布构成。
对于Dirac-GAN,生成器与判别器只拥有一个参数,可见图1所示。那么,训练的目标函数为
$$
\begin{aligned}
L(\theta,\psi)=f(\psi\theta)+f(0)
\end{aligned}
$$
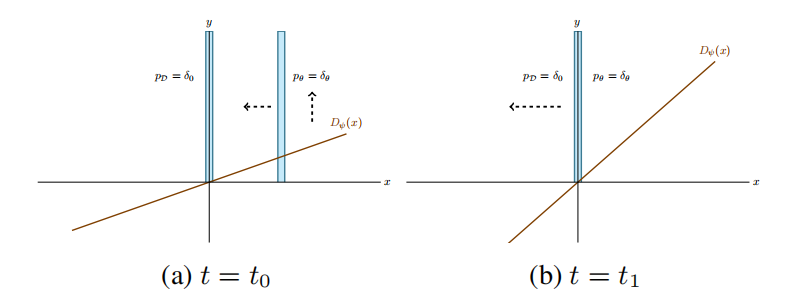
图1 基于梯度下降的GAN优化永远无法拟合的反例可视化
虽然线性分类器可能具有限制性,但是在该例子中线性分类器的能力与所有真实值函数一致:若利用$f(t)=-log(1+exp(-t))$,那么取式(4)的极值,可得到$p_{\theta}$与$p_{\mathcal{D}}$之间的$JS-Divergence$。若利用$f(t)=t$且对分类器施加Lipschitz约束,那么对于Wasserstein-divergence也保持该特性。这个论断在后面也有相应的讨论。
作者们表示:在该简单常见下,GANs的训练动力学无法拟合。
引理2.2. 训练目标函数式(4)的平衡点在$\theta=\psi=0$取得。此外,平衡点处的梯度向量场的雅可比有两个特征值$\pm{f}'(0)i$,均在虚轴上。
根据引理2.2,在式(3)的连续系统中,Dirac-GAN虽然通常不会线性速率拟合,但可能次线性速率拟合。然而,引理2.3表示其不会拟合。
引理2.3. $v(\theta,\psi)$的梯度向量场的积分曲线不会拟合到Nash均衡。确切的说,梯度向量场$v(\theta,\psi)$的每个积分曲线$(\theta(t),\psi(t))$满足$\theta(t)^2+\psi(t)^2=const$。
引理2.3,简单理解就是:沿着梯度方向移动,只会转圈圈。其中,梯度向量场的积分曲线是指沿着梯度方向移动。
然而,该结果与相关论文结果并不矛盾。这是因为反例违反了Gradient descent GAN optimization is locally stable中假设$IV$,其要求在均衡点附近生成器分布与真实数据分布一致。同时,也违反了TTUR中假设:最优分类器参数向量是当前生成器参数的连续函数。实际上,除非$\theta=0$,否则Dirac-GAN不存在最优分类器。即使作者们利用TTUR中两倍规模的更新,也无法拟合到Nash均衡。然而,这个例子可以说是GAN训练中典型的例子,这是因为处理的真实数据主要聚焦于低维流形。

图2 Dirac-GAN的训练行为。起始点标记为红色
接下来,在离散场景下观察一下该反例。
引理2.4. 对于同步梯度下降,更新运算$F_h(\theta,\psi)$的雅可比在均衡点的特征值$\lambda_{1/2}=1\pm h{f}'(0)i$,其绝对值为$\sqrt{1+h^2{f}'(0)^2}$。与学习率无关,同步梯度下降在均衡点附近不稳定。甚至,对于初始条件和学习率$h\gt0$,同步梯度下降获得的$(\theta_k,\psi_k)$是单调增加的。
如图2a所示,同步梯度下降的行为。
类似的,在交替梯度下降情况下,训练动力学为:
引理2.5. 对于交替梯度下降,其生成器的更新次数$n_g$和判别器的更新次数$n_d$,运算$F_h(\theta,\psi)$的雅可比的特征值为
$$
\begin{aligned}
\lambda_{1/2}=1-\frac{\alpha^2}{2}\pm\sqrt{(1-\frac{\alpha^2}{2})^2-1}
\end{aligned}
$$
其中$\alpha:=\sqrt{n_gn_d}h{f}'(0)$。对于$\alpha\le2$,所有特征值在单位球上。若$\alpha\gt2$,所有特征值在单位球外。
即使引理2.5. 也表明交替梯度下降不会线性速度拟合到Nash均衡,原则上可次线性速度拟合。然而,这是不可能的,因为即使连续系统也不会拟合。作者们通过实验也发现:交替梯度下降法只会在均衡点周围的稳定圆上震荡,不存在收敛的迹象,可见图2b所示。
总结
绕了这么一大圈,作者想表达的是在数据分布为低维流形的情况下,基于经典梯度下降算法无法使GAN收敛到Nash均衡点。
引用方法
请参考:
li,wanye. "哪种训练方法导致GANs真实的拟合 (一)?". wyli'Blog (Oct 2024). https://www.robotech.ink/index.php/archives/640.html
或BibTex方式引用:
@online{eaiStar-640,
title={哪种训练方法导致GANs真实的拟合 (一)?},
author={li,wanye},
year={2024},
month={Oct},
url="https://www.robotech.ink/index.php/archives/640.html"
}