sCMs:连续时间一致性模型的进阶
一致性模型 (Consistency Model, CM)属于一类可实现快速采样的扩散生成模型。然而,利用离散化时间步训练的一致性模型,往往需要引入辅助参数且容易产生离散化误差,从而造成样本质量不佳。与之相对的,连续时间范式的模型缓和了该问题,但会产生训练的不稳定性。为了解决该问题,sCMs作者们提出了TrigFlow范式,统一了EDM和Flow Matching,显著简化了扩散模型范式。在该基础上,分析了CM训练不稳定的根本原因,且提出了improved time-conditioning和自适应group normalization用于缓解该问题。除此之外,作者们也重新阐释了连续时间的CMs,其包含关键项自适应权重与正则化,以及可产生稳定训练和可扩展训练的渐进衰退。
基于这些方法,作者们提升了一致性模型在一致性训练和蒸馏方面的性能,实现了与之前离散化范式可媲美或更优的结果。作者们也表明该模型(sCMs)的高效扩展性,实现了一个可预测的更优采样质量。此外,与SOTA扩散模型相比,sCMs利用两步生成把FID间隔缩小到了$10\%$。作者们证明了随着相邻时间间隔缩小至接近连续时间,连续时间CMs相比离散时间拥有更好的采样质量。
相关理论
扩散模型
给定训练集,$p_d$表示数据的潜在分布,$\sigma_d$表示标准差。扩散模型通过逆噪音化过程生成样本。其中,噪音过程可渐近的扰动数据样本$s_0\sim p_d$为噪音$x_t=\alpha_t x_0+\sigma_tz_t$,且$z_t\sim\mathcal{N}(0,I)$为标准高斯噪音。随着$t\in[0,T]$的增加,扰动也增加。
扩散模型两种范式EDM和Flow Matching
EDM:噪音过程中$\alpha_t=1$和$\sigma_t=t$,训练目标为$\mathbb{E}_{x_0,z,t}[w(t)\Vert f_{\theta}(x_t,t)-x_0\Vert_2^2]$,其$w_t$为权重函数。扩散模型被参数化为$f_{\theta}(x_t,t)=c_{skip}(t)x_t+c_{out}(t)F_{\theta}(c_{in}(t)x_t,c_{noise}(t))$。其中,$F_{\theta}$是参数为$\theta$的神经网络,$c_{skip},c_{out},c_{in}$以及$c_{noise}$为可确保初始化时训练目标在时间步之间拥有单位方差的人工设计系数。在采样时,EDM求解概率流ODE$\frac{dx_t}{dt}=[x_t-f_{\theta}(x_t,t)]/t$,起始点为$x_t\sim\mathcal{N}(0,T^2I)$和停止时间点$x_0$。
Flow Matching:噪音过程利用可微分系数$\alpha_t$和$\sigma_t$,时间导数${\alpha}'_t$和${\sigma}'_t$ 。通常,$\alpha_t = 1-t,\sigma_t = t$ 。训练目标为$\mathbb{E}_{x_0,z,T}[w(t)\Vert F_{\theta}(x_t,t)-({\alpha}'_tx_0+{\sigma}'_tz)\Vert_2^2]$。其中,$w_t$为权重函数。采样过程从时刻$t=1$的$x_1\sim\mathcal{N}(0,I)$开始,求解概率流常微分方程$\frac{dx_t}{dt}=F_{\theta}(x_t,t)$
Plus: 从这里可以看到扩散模型的时间调度是离散的,且时刻$t\gt1$开始。然而,流匹配模型属于连续的,且时间调度范围为$t\in[0,1]$。对于目标函数,扩散模型的目标函数为拟合真实数据,而流匹配模型的目标为拟合概率流。
一致性模型
一致性模型训练的是映射噪音$x_t$和对应数据$x_0$的神经网络。一个有效的$f_{\theta}$应满足边界条件$f_{\theta}(x,0)\equiv x$。一种满足该条件的方式是参数化一致性模型为$f_{\theta}(x_t,t)=c_{skip}(t)x_t+c_{out}(t)F_{\theta}(c_{in}(t)x_t,c_{noise}(t))$,且$c_{skip}(0)=1,c_{out}(0)=0$。一致性模型的训练目标是相邻时间步之间拥有一致性输出。取决于时间步的选择,一致性模型被分为:

图1 离散时间一致性模型和连续时间一致性模型
离散时间 CMS:训练目标被定在两个连续时间步之间
$$ \begin{aligned} \mathbb{E}_{x_t,t}[w(t)d(f_{\theta}(x_t,t),f_{\theta^{-}}(x_{t-\Delta t},t-\Delta t))] \end{aligned}\tag{1} $$
式中$\theta^{-}$表示stopgrad$(\theta)$,$w(t)$为权重函数,$\Delta t\gt0$表示相邻时间步之间的距离,以及$d(\cdot,\cdot)$为度量函数。通常,度量函数为$l_2$损失$d(x,y)=\Vert x-y\Vert_2^2$,Pseudo-Huber损失$d(x,y)=\sqrt{\Vert x-y\Vert_2^2+c^2}-c$且$c\gt0$,以及LPIPS损失。离散一致性模型对$\Delta t$的选择很敏感,容易产生离散化误差,因此需要人工设计衰退调度。
连续时间 CMs:若利用$d(x,y)=\Vert x-y\Vert_2^2$,且$\Delta t\to 0$,那么式(1)关于$\theta$的梯度拟合至
$$ \begin{aligned} \nabla_{\theta}\mathbb{E}_{x_t,t}[w(t)f_{\theta}^T(x_t,t)\frac{df_{\theta^{-}}(x_t,t)}{dt}] \end{aligned}\tag{2} $$
其中,$\frac{df_{\theta^{-}}(x_t,t)}{dt}=\nabla_{x_t}f_{\theta^{-}}(x_t,t)\frac{dx_t}{dt}+\partial_tf_{\theta^{-}}(x_t,t)$为$f_{\theta^{-}}$在$(x_t,t)$处的正切。显而易见,连续时间的一致性模型不取决于ODE求解器,由此避免了离散化误差且提供了训练期间更多的精确监督信号。
简化连续时间一致性模型
之前的一致性模型采用EDM中的模型参数化和扩散过程。然而,EDM的扩散过程是方差爆炸的,即$x_t=x_0+tz_t$,作者们推导出$c_{skip}(t)=\frac{\sigma_d^2}{t^2+\sigma_d^2},c_{out}(t)=\sigma_d\cdot t/\sqrt{\sigma_d^2+t^2}$以及$c_{in}(t)=1/\sqrt{t^2+\sigma_d^2}$。虽然这些系数对训练效率很重要,但$t$与$\sigma_d$之间复杂算法关系复杂化了CMs的理论分析。
为了简化EDM以及CMs,作者们提出了TrigFlow,一种保持EDM特性的扩散模型,且满足$c_{skip}(t)=cos(t),c_{out}(t)=sin(t)$以及$c_{in}(t)\equiv1/\sigma_d$。同时,TrigFlow属于flow matching和v-prediction参数化的特殊情况。因此,该扩散范式可同时结合EDM和Flow Matching的优势,即允许扩散过程、扩散模型参数化、PF-ODE、扩散训练目标、以及CM参数化。
扩散过程:给定$x_0\sim p_d(x_0)$和$z\sim\mathcal{N}(0,\sigma_d^2I)$,噪音样本被定义为$x_t=cos(t)x_0+sin(t)z$,且$t\in[0,\frac{\pi}{2}]$。特别的,先验样本$x_{\frac{\pi}{2}}\sim\mathcal{N}(0,\sigma_d^2I)$
扩散模型与概率流-ODE:扩散模型参数化为$f_{\theta}(x_t,t)=F_{\theta}(x_t/\sigma_d,c_{noise}(t))$,对应的PF-ODE为
$$ \begin{aligned} \frac{dx_t}{dt}=\sigma_dF_{\theta}(\frac{x_t}{\sigma_d},c_{noise}(t)) \end{aligned}\tag{3} $$
扩散目标函数:
$$ \begin{aligned} \mathcal{L}_{Diff}(\theta)=\mathbb{E}_{x_0,z,t}[\Vert\sigma_d F_{\theta}(\frac{x_t}{\sigma_d},c_{noise}(t))-v_t\Vert_2^2] \end{aligned}\tag{4} $$
式中$v_t=cos(t)z-sin(t)x_0$
一致性模型:一个有效的CM满足边界条件$f_{\theta}(x,0)\equiv x$。为了实现该条件,利用一阶ODE求解器参数化CM为式(3)中概率流常微分方程的单步生成方案。确切的说,参数化为
$$ \begin{aligned} f_{\theta}(x_t,t)=cos(t)x_t-sin(t)\sigma_dF_{\theta}(\frac{x_t}{\sigma_t},c_{noise}(t)) \end{aligned}\tag{5} $$
式中$c_{noise}(t)$为时间的变化。
Plus:这里在介绍TrigFlow,只是省去了公式推导。
稳定化连续时间一致性模型
为了构建稳定化连续时间CMs的训练,作者们对参数化、网络架构、以及训练目标进行了改进。
参数化与网络架构
训练连续时间CMs的关键是式(2),其取决于正切函数$\frac{df_{\theta^{-}}(x_t,t)}{dt}$。在TrigFlow下,正切函数为
$$ \begin{aligned} \frac{df_{\theta^{-}}(x_t,t)}{dt}=-cos(t)(\sigma_dF_{\theta^{-}}(\frac{x_t}{\sigma_d},t)-\frac{dx_t}{dt})-sin(t)(x_t+\sigma_d\frac{dF_{\theta^{-}}(\frac{x_t}{\sigma_d},t)}{dt}) \end{aligned}\tag{6} $$
式中$\frac{dx_t}{dt}$表示概率流常微分方程,在一致性蒸馏中利用预训练扩散模型估计,或者在一致性训练中利用无偏估计器估计。
为了稳定化训练,确保式(6)中正切函数在不同时间步属于稳定的很有必要。实验中,发现$\sigma_dF_{\theta^{-}}$,概率流常微分方程(PF-ODE)$\frac{dx_t}{dt}$,以及噪音样本$x_t$均属于相对稳定的。那么,正切函数中就剩下$sin(t)\frac{dF_{\theta^{-}}}{dt}=sin(t)\nabla_{x_t}F_{\theta^{-}}\frac{dx_t}{dt}+sin(t)\partial_tF_{\theta^{-}}$。在进一步分析之后,发现$\nabla_{x_t}F_{\theta^{-}}\frac{dx_t}{dt}$属于well-conditioned,那么不稳定性来源于时间导数$sin(t)\partial_tF_{\theta^{-}}$,可被分解为
$$ \begin{aligned} sin(t)\partial_tF_{\theta^{-}}=sin(t)\frac{\partial c_{noise}(t)}{\partial t}\cdot\frac{\partial emb(c_{noise})}{\partial c_{noise}}\cdot\frac{\partial F_{\theta^{-}}}{\partial emb(c_{noise})} \end{aligned}\tag{7} $$
式中$emb(\cdot)$表示时间的编码,通常为位置编码或Fourier编码。
Identity Time Transformation$(c_{noise}(t)\equiv t)$:大部分存在的CMs利用EDM范式,均可被直接迁移到TrigFlow范式。尤其是,时间变化为$c_{noise}(t)=log(\sigma_d tan(t))$,那么导数$sin(t)\cdot\partial_tc_{noise}(t)=1/cos(t)$,在$t\to\frac{\pi}{2}$时趋向于$\infty$,造成了不稳定。因此,作者们提出利用$c_{noise}(t)=t$作为默认时间变换。
Positional Time Embeddings:对于时间编码的通用形式$emb(c)=sin(s\cdot 2\pi w\cdot c+\phi)$,那么$\partial_{c}emb(c)=s\cdot2\pi w~cos(s\cdot2\pi w\cdot c+\phi)$。在大的Fourier规模$s$下,导数拥有更大的幅度且非常振荡,引起不稳定性。为了避免这种情况,作者们利用了位置编码,且与$s\approx0.02$中Fourier编码一致。在论文中Improved Techniques for Training Consistency Models提供了一个原则性解释。
Adaptive Double Normalization:论文Improved Techniques for Training Consistency Models中,作者们发现AdaGN层,被定义为$y=norm(x)\bigodot s(t)+b(t)$,负面的影响了CM训练。因此作者们利用了自适应double normalization,被定义为$y=norm(x)\bigodot pnorm(s(t)+pnorm(b(t)))$,其$pnorm(\cdot)$为Pixel Normalization。
如图2所示,以上三种稳定化方法的效果。
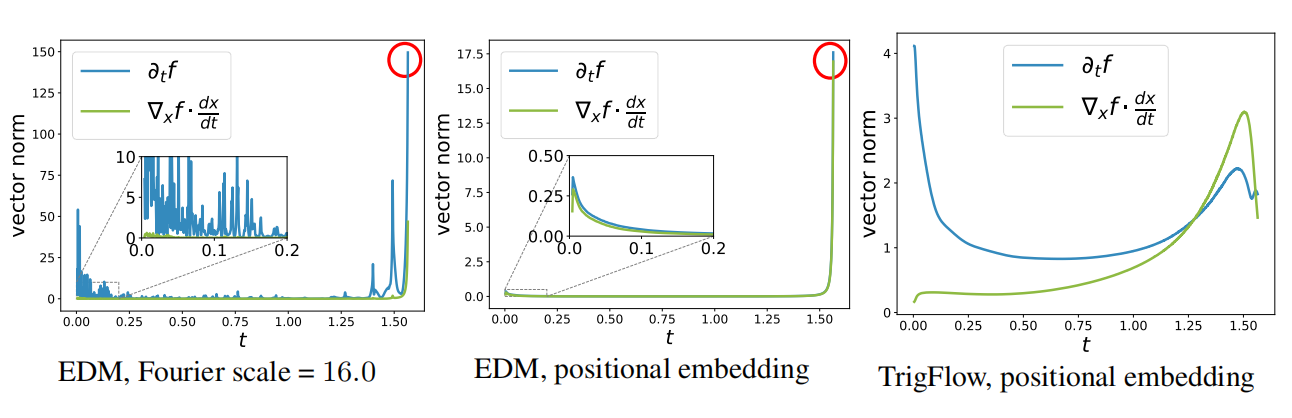
图2 不同范式的稳定性
目标函数
在TrigFlow范式和稳定化方法下,连续时间CM训练的梯度变为
$$ \begin{aligned} \nabla_{\theta}\mathbb{E}_{x_t,t}[-w(t)\sigma_d sin(t)F_{\theta}^{T}(\frac{x_t}{\sigma_d},t)\frac{df_{\theta^{-}}(x_t,t)}{dt}] \end{aligned}\tag{8} $$

图3 一致性蒸馏不同目标函数的比较
为了控制梯度以提升稳定性,作者们提出了以下技术:
Tangent Normalization:一致性训练中大部分梯度方差来源于正切函数$\frac{df_{\theta^{-}}}{dt}$。通过利用$\frac{df_{\theta^{-}}}{dt}/(\Vert\frac{df_{\theta^{-}}}{dt}\Vert+c)$替换$\frac{df_{\theta^{-}}}{dt}$对正切函数进行标准化,其$c=0.1$。一种可替代的方式是在$[-1,1]$内对正切函数进行clip。如图5(a)所示,标准化或clipping导致连续时间CMs的大幅度提升。
Adaptive Weighting:在CM训练中,之前的工作人工设计权重函数$w(t)$,这对于不同的数据分布和网络架构属于次优的。根据EDM2,作者们提出自适应权重函数,这不仅消除了超参数调优的负担,也超越了人工设计权重函数的性能。由于$\nabla_{\theta}\mathbb{E}[F_{\theta}^Ty]=\frac{1}{2}\nabla_{\theta}\mathbb{E}[\Vert F_{\theta}-F_{\theta^{-}}+y\Vert_2^2]$,$y$属于独立于$\theta$的任意向量,那么在基于式(2)训练连续时间CMs时设定$y=-w(t)\sigma_dsin(t)\frac{df_{\theta^{-}}}{dt}$,由此可把式(2)转化为MSE目标函数的梯度。因此,作者们利用与EDM2相同的方式训练一个自适应函数,用于最小化时间步之间MSE损失的方差。在实践中,作者们发现整合一个先验权重$w(t)=\frac{1}{\sigma_dtan(t)}$可进一步降低训练方差。通过包含先验权重,训练网络$F_{\theta}$和自适应权重函数$w_{\phi}(t)$可通过最小化
$$ \begin{aligned} \mathcal{L}_{sCM}(\theta,\phi):=\mathbb{E}_{x_t,t}[\frac{e^{w_{\phi}(t)}}{D}\Vert F_{\theta}(\frac{x_t}{\sigma_d},t)-F_{\theta^{-}}(\frac{x_t}{\sigma_d},t)-cos(t)\frac{df_{\theta^{-}}(x_t,t)}{dt}\Vert_2^2-w_{\phi}(t)] \end{aligned}\tag{9} $$
Diffusion Finetuning and Tangent Warmup:对于一致性蒸馏,作者们发现对预训练扩散模型的微调CM可加速拟合。在式(6)中,正切函数$\frac{df_{\theta^{-}}}{dt}$中$sin(t)(x_t+\sigma_d\frac{dF_{\theta^{-}}}{dt})$引起了不稳定性。为了减轻该问题,作者们利用$r\cdot sin(t)$替换$sin(t)$逐渐warm up该项,其$r$在前$10k$训练迭代中逐渐从$0$增加到$1$。
综合所有这些技术,离散时间和连续时间CM训练的稳定性训练可大幅度提升。如图5(c)所示,增加离散时间CM中的离散化步骤$N$可通过减少离散化误差来提高样本质量,但一旦$N$变得太大($N\gt 1024$ 之后)就会降低,从而出现数值精度问题。相比之下,连续时间CM在所有$N$上的表现都明显优于离散时间CM,这为选择连续时间CM而不是离散时间CM提供了强有力的理由。因此,sCM模型中s表示simple, stable, and scalable,可见算法1。

扩展连续时间一致性模型
大规模扩散模型的训练常见场景包含FP16和Flash Attention。为了提升训练一致性模型时正切$\frac{df_{\theta^{-}}}{dt}$,作者们提升了数值精确性和内存高效的注意力计算,分别是JVP Rearrangement和JVP of Flash Attention。
JVP Rearrangement:计算$\frac{df_{\theta^{-}}}{dt}$包含$\frac{dF_{\theta^{-}}}{dt}=\nabla_{x_t}F_{\theta^{-}}\cdot\frac{dx_t}{dt}+\partial_tF_{\theta^{-}}$,其可通过Jacobian-vector乘积(JVP)对输入向量$(x_t,t)$的$F_{\theta^{-}}$和正切向量$(\frac{dx_t}{dt},1)$进行高效计算得到。然而,作者们发现在$t\to0$或$t\to\frac{\pi}{2}$正切的计算在中间层会发生溢出。为了提升树枝精确性,作者们提出重新分配正切的计算。确切的说,由于式(9)中包含$cos(t)\frac{df_{\theta}^{-}}{dt}$且$\frac{df_{\theta^{-}}}{dt}$成比例于$sin(t)\frac{dF_{\theta^{-}}}{dt}$,那么
$$ \begin{aligned} cos(t)sin(t)\frac{dF_{\theta^{-}}}{dt}=(\nabla_{\frac{x_t}{\sigma_d}}F_{\theta^{-}})\cdot(cos(t)sin(t)\frac{dx_t}{dt})+\partial_t F_{\theta^{-}}\cdot(cos(t)sin(t)\sigma_d) \end{aligned}\tag{10} $$
这种重新分配极大减轻了中间层的溢出问题,且导致FP16的训练更稳定。
JVP of Flash Attention:在大规模注意力计算中,Flash Attention被广泛地应用。然而,该算法无法计算JVP。为此,在一次前向过程中作者们提出了相似的算法不仅可高效的计算softmax注意力,也可高效的计算JVP。
引用方法
请参考:
li,wanye. "sCMs:连续时间一致性模型的进阶". wyli'Blog (Oct 2024). https://www.robotech.ink/index.php/archives/657.html
或BibTex方式引用:
@online{eaiStar-657,
title={sCMs:连续时间一致性模型的进阶},
author={li,wanye},
year={2024},
month={Oct},
url="https://www.robotech.ink/index.php/archives/657.html"
}
CC版权: 本篇博文采用《CC 协议》,转载必须注明作者和本文链接
博主太厉害了!