Stable Diffusion3:扩展Rectified Flow Transformers
扩散模型从噪音中生成数据,已经成为从自然语言中生成高分辨率图片和视频的标准方式。然而,扩散模型的迭代性本质造成了很大的计算成本,以及推理时较长的采样时间。为了提升扩散模型的效率,研究人员也提出了很多模型,例如:Consistency Model,但需要考虑采样路径选择的问题。这是因为路径的选择对采样有很重要的影响,例如:论文Common Diffusion Noise Schedules and Sample Steps are Flawed表明无法从数据中移除所有噪音的路径可能导致训练数据与测试数据之间分布的差异,甚至导致伪影的产生。同时,前向过程的选择也影响着反向过程的采样效率。
前向路径的一个特别选择是Rectified Flow,该方法通过直线的方式连接数据与噪音。虽然该模型的优势已经在实验上得到证明(可见论文:SiT: Exploring Flow and Diffusion-based Generative Models with Scalable Interpolant Transformers),但是这些大部分局限于类条件模型。
在此基础上,Stable Diffusion3论文Scaling Rectified Flow Transformers for High-Resolution Image Synthesis作者们提升了训练rectified flow模型的噪音采样技术。同时,作者们发现固定的文本表示直接用于模型是不理想。因此,设计了新的架构,可容纳图片和文本tokens的可学习流。不仅如此,作者们研究了新架构和新采样方式结合下的模型扩展性。实验证明了验证损失的一个可预测扩展趋势,也表明了更低的验证损失与提升自动的评估和人类评估强相关。
Flows的Simulation-Free训练
假设把生成模型定义为噪音分布$p_1$中样本$x_1$到数据分布$p_0$中样本$x_0$之间的映射。该映射可定义为常微分方程
$$ \begin{aligned} dy_t=v_{\Theta}(y_t,t)dt \end{aligned}\tag{1} $$
其中,速度$v$被参数化为权重为$\Theta$的神经网络。
然而,通过ODE求解器直接求解式(1)实际上计算成本很高。一种高效的方式是近似可生成$p_0$和$p_1$之间概率路径的向量场$u_t$。其中,概率路径实际上可以理解为ODE的解。
Plus:根据笔者的理解,向量场应该是指从噪音到真实数据的路径上所经过的向量构成的集合。每个向量均有方向,那么向量形成的集合就是一个场。
为了构建向量场$u_t$,定义一个前向过程为
$$ \begin{aligned} z_t=a_tx_0+b_t\epsilon~where~\epsilon\sim\mathcal{N}(0,I) \end{aligned}\tag{2} $$
该前向过程对应的是一条$p_0$与$p_1=\mathcal{N}(0,1)$概率路径$p_t$。
在$a_0=1,b_0=0,a_1=0,b_1=1$情况下,边缘分布
$$ \begin{aligned} p_t(z_t)=\mathbb{E}_{\epsilon\sim\mathcal{N}(0,I)}p_t(z_t\vert\epsilon) \end{aligned}\tag{3} $$
与数据分布和噪音分布一致。
为了形式上清晰的表达$z_t,x_0$以及$\epsilon$之间的关系,引入$\psi_t$和$u_t$
$$ \begin{aligned} \psi_t(\cdot\vert\epsilon):x_0\to a_tx_0+b_t\epsilon\\ u_t(z\vert\epsilon):={\psi}'_t(\psi_t^{-1}(z\vert\epsilon)\vert\epsilon) \end{aligned}\tag{4} $$
此时,$z_t,u_t$和$p_t$实际上属于等价关系,均可被理解为ODE的解或概率路径。根据Flow-Matching,边缘向量场$u_t$可利用条件向量场$u_t(\cdot\vert\epsilon)$构建
$$ \begin{aligned} u_t(z)=\mathbb{E}_{\epsilon\sim\mathcal{N}(0,I)}u_t(z\vert\epsilon)\frac{p_t(z\vert\epsilon)}{p_t(z)} \end{aligned}\tag{5} $$
由于式(5)中边缘化的存在,直接基于Flow-Matching目标函数回归$u_t$很困难
$$ \begin{aligned} \mathcal{L}_{FM}=\mathbb{E}_{\epsilon\sim\mathcal{N}(0,I)}\Vert v_{\Theta}(z,t)-u_t(z)\Vert \end{aligned}\tag{6} $$
plus: 这里的计算复杂很高,可能是因为每次边缘化都需要求加权平均带来的。
基于条件向量场的条件Flow Matching可提供等价且可行的目标函数
$$ \begin{aligned} \mathcal{L}_{CFM}=\mathbb{E}_{t,p_t(z\vert\epsilon),p(\epsilon)}\Vert v_{\Theta}(z,t)-u_t(z\vert\epsilon)\Vert \end{aligned}\tag{7} $$
为了把损失函数转为确切的形式,对式(3)引入${\psi}'(x_0\vert\epsilon)={a}'_tx_0+{b}'_t\epsilon$和${\psi_t}'(z\vert\epsilon)=\frac{z-b_t\epsilon}{a_t}$
$$ \begin{aligned} {z}'_t=u_t(z_t\vert\epsilon)=\frac{{a}'_t}{a_t}z_t-\epsilon b_t(\frac{{a}'_t}{a_t}-\frac{{b}'_t}{b_t}) \end{aligned}\tag{8} $$
若定义信噪比为$\lambda_t:=log\frac{a^2_t}{b_t^2}$,那么
$$ \begin{aligned} u_t(z_t\vert\epsilon)=\frac{{a}'_t}{a_t}z_t-\frac{b_t}{2}{\lambda}'_t\epsilon \end{aligned}\tag{9} $$
式(9)中${\lambda}'_t=2(\frac{{a}'_t}{a_t}-\frac{{b}'_t}{b_t})$可以理解信噪比的另一种表达形式
由此,式(6)变为
$$ \begin{aligned} \mathcal{L}_{CFM} &=\mathbb{E}_{t,p_t(z\vert\epsilon),p(\epsilon)}\vert v_{\Theta}(z,t)-\frac{{a}'_t}{a_t}z+\frac{b_t}{2}{\lambda}'_t\epsilon\Vert_2^2 \\ &=\mathbb{E}_{t,p_t(z\vert\epsilon),p_{\epsilon}}(-\frac{b_t}{2}{\lambda}'_t)^2\Vert\epsilon_{\Theta}(z,t)-\epsilon\Vert \end{aligned}\tag{10} $$
式(10)中$\epsilon_{\Theta}:=\frac{-2}{{\lambda}'_tb_t}(v_{\Theta}-\frac{{a}'_t}{a_t}z)$
根据式(10),可知,时变的权重不会影响目标函数的最优点。因此,可以推导出提供期望解决方案信号的各种加权损失函数,且不影响优化轨迹。为了便于分析,作者们把目标函数写为
$$ \begin{aligned} \mathcal{L}_w(x_0)=-\frac{1}{2}\mathbb{E}_{t\sim\mathcal{U}(t),\epsilon\sim\mathcal{N}(0,I)}[w_t{\lambda}'_t\Vert\epsilon_{\Theta}(z_t,t)-\epsilon\Vert^2] \end{aligned}\tag{11} $$
式(11)中$w_t=-\frac{1}{2}{\lambda}'_tb_t^2$时对应于$\mathcal{L}_{CFM}$
Flow的轨迹
接下来,作者们描述了以上形式的不同变体
Rectified Flow:把前向过程定义为数据分布和标准正态分布之间的直线路径,即
$$ \begin{aligned} z_t=(1-t)x_0+t\epsilon \end{aligned}\tag{12} $$
损失函数为$\mathcal{L}_{CFM}$时,其$w_t^{RF}=\frac{t}{1-t}$。神经网络直接参数化的是速度$v_{\Theta}$
EDM:前向过程形式定义为
$$ \begin{aligned} z_t=x_0+b_t\epsilon \end{aligned}\tag{13} $$
论文Understanding Diffusion Objectives as the ELBO with Simple Data Augmentation中$b_t=exp~F_{\mathcal{N}}^{-1}(t\vert P_m,P_s^2)$。其中,$F_{\mathcal{N}}^{-1}$为均值为$P_m$和方差为$P_s^2$正态分布的分位数函数。那么,可产生
$$ \begin{aligned} \lambda_t\sim\mathcal{N}(-2P_m,(2P_s)^2)~for~t\sim\mathcal{U}(0,1) \end{aligned}\tag{14} $$
网络通过F预测进行参数化,损失函数$\mathcal{L}_{w_t}^{EDM}$的权重为
$$ \begin{aligned} w_t^{EDM}=\mathcal{N}(\lambda_t\vert-2P_m,(2P_s)^2)(e^{-\lambda_t}+0.5^2) \end{aligned}\tag{15} $$
Cosine:前向过程为
$$ \begin{aligned} z_t=cos(\frac{\pi}{2}t)x_0+sin(\frac{\pi}{2}t)\epsilon \end{aligned}\tag{16} $$
在与$\epsilon$参数化和损失结合之后,这对应于一个权重$w_t=sech(\lambda_t/2)$
Tailored信噪比采样器
Rectified Flow的损失函数在时间步$[0,1]$上均匀的训练速度$v_{\Theta}$。直觉上,速度预测目标$\epsilon-x_0$在中间步骤是最困难。这是由于$t=0$的最优预测为$p_1$的均值,$t=1$的最优预测为$p_0$的均值。因此,需要把关于$t$的均匀分布$\mathcal{U}(t)$改为密度$\pi(t)$的有偏分布,其对应于权重$w_t^{\pi}=\frac{t}{1-t}\pi(t)$的损失函数$\mathcal{L}_{w_t^{\pi}}$
为了对中间时间步赋予更多权重,可通过高频采样的方式实现。接下来,作者们描述了时间步密度$\pi(t)$
Logit-Normal采样:对中间步骤施加更多权重的方式是logit-normal分布
$$ \begin{aligned} \pi_{ln}(t;m,s)=\frac{1}{s\sqrt{2\pi}}\frac{1}{t(1-t)}exp(-\frac{(logit(t)-m)^2}{2s^2}) \end{aligned}\tag{17} $$
式中$logit(t)=log\frac{t}{1-t}$,位置参数$m$,缩放参数$s$。位置参数为负值可使训练时间步骤偏向于数据$p_0$,而正数$m$则偏向于$p_1$。
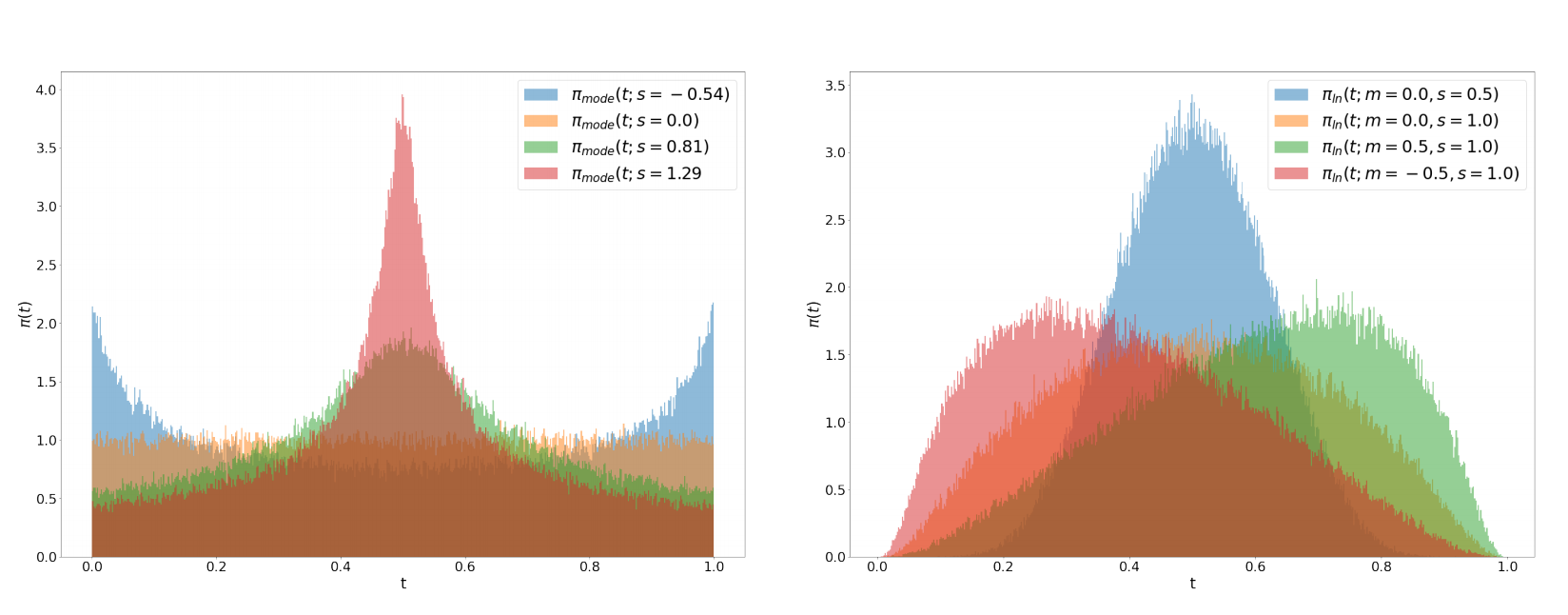
图1 位置参数和缩放参数对分布的影响
如题1所示,缩放参数控制分布的宽度。在实践中,作者们从正太分布$\mathcal{N}(u;m,s)$中采样变量$u$,再把它映射为标准logistic函数。
带有长尾的Mode采样:logit-normal密度总是在端点$0$和$1$处消失。为了研究这对性能是否存在负面效果,作者们利用了一个在$[0,1]$严格正密度的时间步采样分布
$$ \begin{aligned} f_{mode}(u;s)=1-u-s\cdot(cos^2(\frac{\pi}{2}u)-1+u) \end{aligned}\tag{18} $$
式中$s$为缩放系数。
对于$-1\le s\le\frac{2}{\pi-2}$,该函数属于单调的,由此作者们可利用它从隐式密度$\pi_{mode}(t;s)=\vert\frac{d}{dt}f_{mode}^{-1}(t)\vert$中采样。根据图1,可知,在采样时,缩放参数控制着中点或端点有效性。
CosMap:作者们也寻找使log-snr(信噪比)匹配Improved Denoising Diffusion Probabilistic Models中余弦调度$2log\frac{cos(\frac{\pi}{2}u)}{sin(\frac{\pi}{2}u)}=2log\frac{1-f(u)}{f(u)}$的映射$f:u\to f(u)=t,u\in[0,1]$,求解得到
$$ \begin{aligned} t=f(u)=1-\frac{1}{tan(\frac{\pi}{2}u)+1} \end{aligned}\tag{19} $$
对应的密度为为
$$ \begin{aligned} \pi_{CosMap}(t)=\vert\frac{d}{dt}f^{-1}(t)\vert=\frac{2}{\pi-2\pi t+2\pi t^2} \end{aligned}\tag{20} $$
文生图架构
如图2所示,本文的扩散架构。网络架构的设置遵循在预训练自编码器的隐空间训练text-to-image模型的LDM。与Photorealistic Text-to-Image Diffusion Models with Deep Language Understanding相似,作者们把图片编码为隐表示,且利用预训练frozen文本模型编码条件文本$c$。
与DiT架构相似,作者们把时间步$t$的embedding和文本embedding($c_{vec}$)输入到调节机制。在此基础上,为了解决pooled文本表示只保留了粗粒度的信息,构建了序列序列表示$c_{ctxt}$信息。
确切的说,作者们构建了文本和图片的embeddings序列。对于图片,先把隐藏空间的像素表示$x\in\mathbb{R}^{h\times w\times c}$划分为$2\times2$的patches,再把这些patches打平长度为$\frac{1}{2}\cdot h\cdot\frac{1}{2}\cdot w$的patch编码序列。同时,每个patch均加上一个位置编码。在把这些patch编码和文本编码$c_{txt}$映射到共用维度之后,再对两个序列进行concat操作,可见图2a所示。
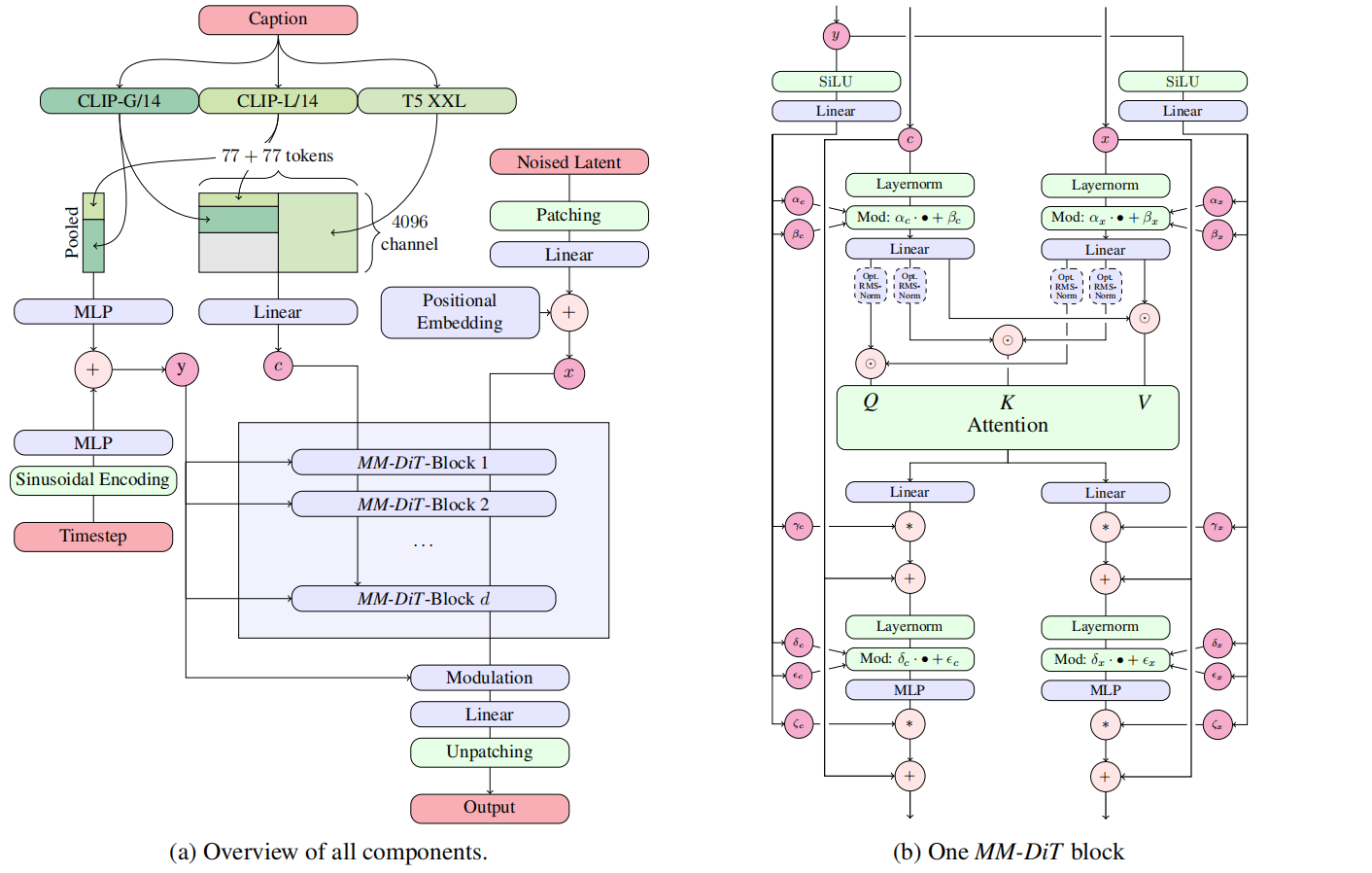
图2 Stable Diffusion3架构。连接用⊙表示,元素乘法用∗表示。可以添加Q和K的RMS-Norm以稳定训练运行
由于文本与图片编码属于不同的模态,因此利用两个独立的权重集处理。如图2b所示,这对应于两个独立的transformer。同时,为了两个表示在自己的空间内考虑彼此,因此加入了两个模态之间的注意力计算。
对于模型扩展实验,作者们把模型深度设置为$d$(注意力模块),隐藏层维度为$64\cdot d$,注意力head的数量为$d$,MLP块的通道扩展为$4\cdot64\cdot d$
总结
对于采样器的改进,根据中间时间步预测最困难的直觉,把采样器由均匀采样变为有偏采样。网络架构的设计综合考虑了各种模态。
引用方法
请参考:
li,wanye. "Stable Diffusion3:扩展Rectified Flow Transformers". wyli'Blog (Oct 2024). https://www.robotech.ink/index.php/archives/653.html
或BibTex方式引用:
@online{eaiStar-653,
title={Stable Diffusion3:扩展Rectified Flow Transformers},
author={li,wanye},
year={2024},
month={Oct},
url="https://www.robotech.ink/index.php/archives/653.html"
}
CC版权: 本篇博文采用《CC 协议》,转载必须注明作者和本文链接