SiT:利用可扩展的Interpolant Transformer探索基于Flow和扩散的生成模型
SoTA扩散模型增量式的把数据转变为高斯噪音,被称为扩散过程,该过程可被建模为把原始数据分布迭代的平滑为正态分布的时变分布。扩散模型的学习目标要么为预测扩散过程中的噪音,要么为预测数据与高斯之间分布的分数。然而,扩散过程限制了数据和高斯之间的联系,直到随机插值的出现。SiT作者们探究了随机插值带来的灵活性对大规模图片生成的影响。除此之外,作者们研究了学习目标的选择和推理时模型的采样问题。基于这些研究,作者们在设计空间中采取一系列正交步骤从扩散模型转换为插值模型。最终,不仅简化了学习问题而且提升了算法性能。
其中,SiT的整个设计空间由时间离散化和模型预测(对应于估计分数和速度部分的内容)、插值选择(对应于确定插值过程的内容)、采样器和扩散系数的选择(对应于确定扩散系数的内容)、以及模型大小构成(对应于插值Transformer架构的内容)。
Flows与Diffusions
Flow和扩散模型均利用随机过程,把噪音$\mathbf{\epsilon}\sim\mathcal{N}(0,I)$逐渐的变为数据$\mathbf{x}_{*}\sim p(x)$。这种时变过程可被表示为
$$
\begin{aligned}
\mathbf{x}_t=\alpha_t\mathbf{x}_{*}+\sigma_t\mathbf{\epsilon}
\end{aligned}\tag{1}
$$
式(1)中$\alpha_t$为$t$的递减函数,而$\sigma_t$为$t$的递增函数。
在随机插值和Flow模型中,$t\in[0,1]$且$\alpha_0=\sigma_1=1,\alpha_1=\sigma_0=0$。
虽然制定随机过程$\mathbf{x}_t$存在细微差别,但是随机插值和基于分数的扩散模型的共同点是:$\mathbf{x}_t$要么利用逆时间随机微分方程采样,要么利用概率流常微分方程采样。
概率流常微分方程:$\mathbf{x}_t$的边缘概率分布$p_t(x)$符合概率流常微分方程分布,其向量场为
$$
\begin{aligned}
\dot{\mathbf{X}}_t=\mathbf{v}(\mathbf{X}_t,t)
\end{aligned}\tag{2}
$$
式中$\mathbf{v}(\mathbf{X}_t,t)$为速度场,由条件期望确定
$$
\begin{aligned}
\mathbf{v}(\mathbf{x},t)&=\mathbb{E}[\dot{\mathbf{x}}_t\vert\mathbf{x}_t=\mathbf{x}]\\
&=\dot{\alpha}_t\mathbb{E}[\mathbf{x}_{*}\vert\mathbf{x}_t=\mathbf{x}]+\dot{\sigma}_t\mathbb{E}[\mathbf{\epsilon}\vert\mathbf{x}_t=\mathbf{x}]
\end{aligned}\tag{3}
$$
通过求解式(2),就可以从$\mathbf{X}_T=\epsilon\sim N(0,I)$生成真实数据。作者们把式(2)称为基于流的生成模型。
与之相比,基于分数的扩散模型通过前向随机微分方程的方式,非直接的设置$\alpha_t$和$\sigma_t$。其中,随机微分方程的均衡分布为$N(0,I)$,即$t\to\infty$时$\mathbf{x}_t$拟合至$N(0,I)$。确切的说,时变概率分布$p_t(\mathbf{x})$符合逆时间随机微分方程分布
$$
\begin{aligned}
d\mathbf{X}_t=\mathbf{v}(\mathbf{X}_t,t)dt-\frac{1}{2}w_t\mathbf{s}(\mathbf{X}_t,t)dt+\sqrt{w_t}d\bar{\mathbf{W}}_t
\end{aligned}\tag{4}
$$
式(4)中$\bar{\mathbf{W}}_t$为逆时间的维纳过程,$w_t\gt0$为任意的时变扩散系数,$\mathbf{v}(\mathbf{x},t)$为式(3)定义的速度,以及$s(\mathbf{x},t)=\nabla logp_t(\mathbf{x})$为分数。与$\mathbf{v}$相似,分数通过条件期望给定
$$
\begin{aligned}
s(\mathbf{x},t)=-\sigma_t^{-1}\mathbb{E}[\epsilon\vert\mathbf{x}_t=\mathbf{x}]
\end{aligned}\tag{5}
$$
求解逆随机微分方程,扩散模型可从$\mathbf{X}_T=\epsilon\sim N(0,I)$生成真实数据。
基于分数的扩散模型与$\alpha_t,\sigma_t$和$w_t$选择有很强的耦合性。与之不同,随机插值模型对$\mathbf{x}_t$和随机微分方程(SDE)之间进行了解耦合,对$\alpha_t,\sigma_t,w_t$的选择更灵活。
Plus:式(3)和式(5)的推导,均在论文的附录中得到了展示。
估计分数与速度
概率流常微分方程和逆时间随机微分方程作为生成模型主要取决于估计速度$\mathbf{v}(\mathbf{x},t)$和分数$\mathbf{s}(\mathbf{x},t)$的能力。根据式(5)可得,基于分数的扩散模型中分数$\mathbf{s}_{\theta}(\mathbf{x},t)$可通过损失函数
$$
\begin{aligned}
\mathcal{L}_{s}(\theta)=\int_{0}^T\mathbb{E}[\Vert \sigma_t\mathbf{s}_{\theta}(\mathbf{x}_t,t)+\epsilon\Vert^2]
\end{aligned}\tag{6}
$$
进行估计。
类似的,式(3)中速度$\mathbf{v}_{\theta}(\mathbf{x},t)$可通过损失函数
$$
\begin{aligned}
\mathcal{L}_{\mathbf{v}}(\theta)=\int_{0}^{T}\mathbb{E}[\Vert\mathbf{v}_{\theta}(\mathbf{x}_t,t)-\dot{\alpha}_t\mathbf{x}_{*}-\dot{\sigma}_t\epsilon\Vert^2]dt
\end{aligned}\tag{7}
$$
对于基于分数的扩散模型来说,随着$T$的增大,时变权重参数越来越重要。与之相比,随机插值中的时变权重变得越来越不重要,但可能引起数值稳定性问题。
基于约束
$$
\begin{aligned}
\mathbf{x}&=\mathbb{E}[\mathbf{x}_t\vert\mathbf{x}_t=\mathbf{x}] \\
&=\alpha_t\mathbb{E}[\mathbf{x}_{*}\vert\mathbf{x}_t=\mathbf{x}]+\sigma_t\mathbb{E}[\epsilon\vert\mathbf{x}_t=\mathbf{x}]
\end{aligned}\tag{8}
$$
那么,式(5)中分数可利用式(3)中速度表达为
$$
\begin{aligned}
\mathbf{s}(\mathbf{x},t)=\sigma_t^{-1}\frac{\alpha_t\mathbf{v}(\mathbf{x},t)-\dot{\alpha}_t\mathbf{x}}{\dot{\alpha}_t\sigma_t-\alpha_t\dot{\sigma}_t}
\end{aligned}\tag{9}
$$
Plus:式(9)的推导可见论文。
根据式(9),速度$\mathbf{v}(\mathbf{x},t)$可利用分数$\mathbf{s}(\mathbf{x},t)$表达,因此可利用该关系确定模型的预测。在实验中,学习了向量场$\mathbf{v}(\mathbf{x},t)$,若利用随机微分方程进行采样,那么利用向量场表示分数。为了保证分母不为0,设定$\dot{\alpha}_t\lt0$和$\dot{\sigma}_t\gt0$。同时,作者们表明:在$t=0$时,$\sigma_t$逐渐消失,$\sigma_{t}^{-1}$引起很大的奇异值,而式(4)中$w_t=\sigma_t$可抵消此奇异值。
确定插值过程
在Flows与Diffusions章节中,呈现了随机插值和基于分数扩散模型的插值($\alpha_t$与$\sigma_t$)通用定义。接下来,确定插值的三个选择。
基于分数的扩散:根据Score-SDE,在前向时间,利用标准的variance-preserving随机微分方程(VP-SDE)
$$
\begin{aligned}
d\mathbf{X}_t=-\frac{1}{2}\beta_t\mathbf{X}_tdt+\sqrt{\beta_t}d\mathbf{W}_t
\end{aligned}\tag{10}
$$
对于$\beta_t\gt0$,$\mathbf{x}_t$的扰动核$p_t(\mathbf{x}_t\vert\mathbf{x}_0)=N(\alpha_t\mathbf{x}_t,\sigma_t^2I)$可被
$$
\begin{aligned}
SBDM-VP:\alpha_t=e^{-\frac{1}{2}\int_{0}^{t}\beta_sds},\quad\sigma_t=\sqrt{1-e^{-\int_0^t\beta_sds}}
\end{aligned}\tag{11}
$$
所定义。式中$SBDM$是指基于分数的扩散模型。
根据式(11),可知,$\beta_t$的选择共同决定$\alpha_t$和$\sigma_t^{2}$。若$\beta_t=1$,那么$\alpha_t=e^{-t},\sigma_t=\sqrt{1-e^{-2t}}$。然而,$\beta_t=1$需要$T$足够大,否则需要搜索更合适的$\beta_t$以减少偏差。确切的说,这种偏差来源于采样时$\epsilon\sim N(0,I)$和式(1)的随机过程密度$\mathbf{x}_1\nsim N(0,I)$不匹配导致的。
通用插值:在随机插值框架下,式(1)的随机过程被确切的定义,且不需要引用任何一个前向随机微分方程,因此在$\alpha_t$和$\sigma_t$的选择上可更灵活。该选择应满足:
- 对于$\forall t\in[0,1]$,$\alpha_t^2+\sigma_t^2\gt0$
- 对于$\forall t\in[0,1]$,$\alpha_t$和$\sigma_t$可微分
- $\alpha_1=\sigma_0=0,\alpha_0=\sigma_1=1$
给定一个过程,在$\mathbf{x}_{t=0}=\mathbf{x}_{*}$和$\mathbf{x}_{t=1}=\epsilon$之间无偏差的插值。在实验中,做出了如下选择
$$
\begin{aligned}
Linear:\quad\alpha_t=1-t,\quad\sigma_t=t, \\
GVP:\alpha_t=cos(\frac{1}{2}\pi t),\sigma_t=sin(\frac{1}{2}\pi t)
\end{aligned}\tag{12}
$$
Generalized Variance Preserving(GVP)是指对于任何具有相同方差的端点分布,其方差在时间上是恒定的。为了学习出$\mathbf{v}(\mathbf{x},t)$和$\mathbf{s}(\mathbf{x},t)$,$\alpha_t$和$\sigma_t$需要在学习前确定。
确定扩散系数
与$\alpha_t$和$\sigma_t$不同,扩散系数$w(t)$不需要学习前确定。对于基于分数的扩散模型($SBDM$),式(4)的扩散系数必须与式(10)的相匹配。在随机插值框架下,只需要保证$w_t\ge0$即可。在实验中,作者们通过考虑如下选择:
- $w_t=\sigma_t$;以抵消时刻$0$奇异值的产生。
- $w_t=sin^2(\pi t)$;不仅可抵消时刻$t=0$的奇异值,且允许在采样时探索时刻接近$t=1$的扩散性消除。
- $w_t$被选择以最小化$D_{KL}(p(\mathbf{x})\Vert p_0(\mathbf{x}))$,$p(\mathbf{x})$表示真实数据分布,$p_0(\mathbf{x})$指时刻$t=0$时$\mathbf{x}_t$的密度。在不考虑式(4)仿真成本的情况下,可进行如下选择
$$
\begin{aligned}
w_t=w_t^{KL}\equiv 2(\dot{\sigma}_t\sigma_t-\frac{\dot{\alpha}_t\sigma_t^2}{\alpha_t})
\end{aligned}\tag{13}
$$
在SBDM-VP插值下,$w_t^{KL}$与$\beta_t$一致。
- 若3中SDE由于在$t=1$时$w_t^{KL}$的幅度而无法整合,那么可正则化扩散系数减少整合成本。例如:若$t\to1$时$w_t^{KL}\to\infty$(式(13)中$\alpha_t$存在于分母),那么Linear和GVP插值可能产生困难。对于式(4)的整合成本,最优的正则化器为
$$
\begin{aligned}
w_t^{KL,\eta}\equiv w_t^{KL}\sqrt{\frac{\mathcal{L}_t}{\mathcal{L}_t+2\eta(w_t^{KL})^2}}
\end{aligned}\tag{14}
$$
式中$\mathcal{L}_t$为$\mathcal{L}_{\mathbf{v}}$在时刻$t$的取值,$\eta$为非负常量。对于分数模型,根据式(9)转换为速度场,再计算对应的$\mathcal{L}_{\mathbf{v}}$。若$t\to1$,若$t\to1$,那么$w_t^{KL,\eta}$在$\sqrt{\frac{\mathcal{L}_{t\to1}}{2\eta}}$处接近于极限。若$\mathcal{L}_t$在$[0,1]$上定义的较好,那么$w_t^{KL,\eta}$在$[0,1]$上表现也很好。
插值Transformer架构
为了聚焦于其它模块的研究,SiT采用了DiT的网络架构。为了降低计算复杂度,与Stable Diffusion相似,SiT也属于一个隐式生成模型,利用了Stable Diffusion中的预训练VAE编码器和解码器。首先,SiT通过'ptachifying'把空间输入$z$处理为$T$个维度为$d$的线性编码tokens。然后,再对这些tokens利用标准的ViT线性位置编码。整个模型由$N$个SiT的transformer块构成,每个维度为$d$。
Plus:笔者认为这里的transformer块应该是指VAE块。
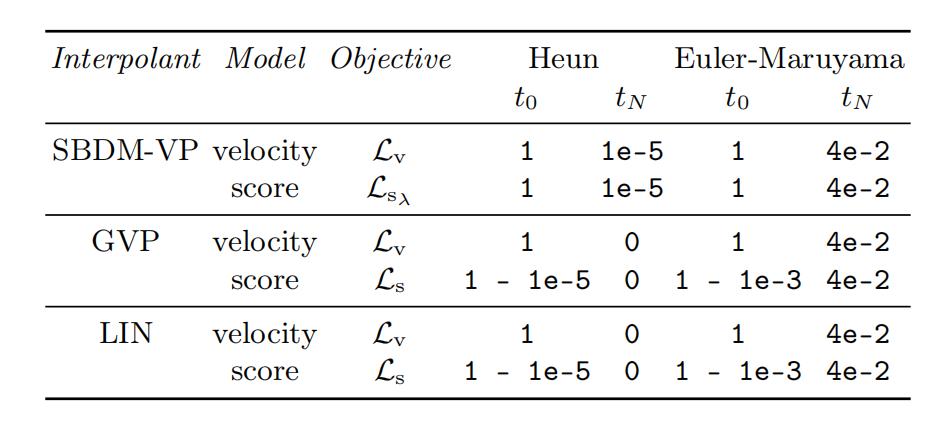
SiT在模型大小上拥有$\{S,B,L,XL\}$四种,与DiT的选择一致。如表1所示,SiT模型的细节。对于ImageNet上的类条件生成,利用AdaLN-Zero块处理条件信息(时间和类标签)。如表2所示,采样器的配置。
表1 SiT模型的细节
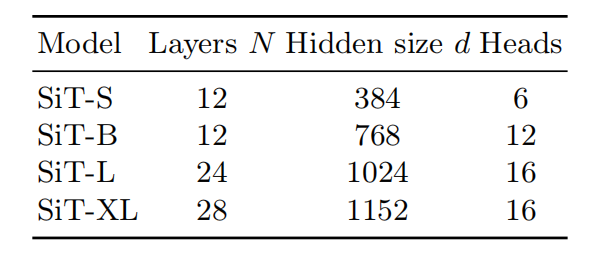
表2 采样器的配置
引用方法
请参考:
li,wanye. "SiT:利用可扩展的Interpolant Transformer探索基于Flow和扩散的生成模型". wyli'Blog (Nov 2024). https://www.robotech.ink/index.php/archives/663.html
或BibTex方式引用:
@online{eaiStar-663,
title={SiT:利用可扩展的Interpolant Transformer探索基于Flow和扩散的生成模型},
author={li,wanye},
year={2024},
month={Nov},
url="https://www.robotech.ink/index.php/archives/663.html"
}