奖励中心化可大幅降低智能体样本复杂度

在持续性问题中，智能体与环境的交互无法被分为子序列或episodes。那么，评估智能体表现的方式有两种，分别是度量平均奖励和累积折扣奖励。论文Reward Centering的作者们表明从每步的观测奖励中估计和减去平均奖励可显著提升基于折扣方法的智能体的性能。同时，作者们表明奖励中心化的含义有：

• 平均中心化奖励从价值估计中移除了一个独立于状态的常量，从而使价值函数近似器聚焦于状态与动作之间的相对区别。
• 平均中心化奖励使标准方法对奖励中的常量偏置具有更强的鲁棒性。这对奖励信号不可知或变化的场景非常有用。

奖励中心化理论

通过Laurent级数分解，折扣的价值函数$v^{\gamma}_{\pi}=\mathbb{E}[\sum_{t=0}^{\infty}\gamma^tR_{t+1}\vert S_t=s,A_{t:\infty}\sim\pi]$可被分解为两个部分，其中一个是不取决于状态或动作的常量，即不参与动作的选择。数学上，对于策略$\pi$的表格型折扣价值函数$v_{\pi}^{\gamma}:\mathcal{S}\to\mathbb{R}$可分解为
$$
\begin{aligned}
v_{\pi}^{\gamma}(s)=\frac{r(\pi)}{1-\gamma}+\tilde{v}_{\pi}(s)+e_{\pi}^{\gamma}(s),~\forall s,
\end{aligned}\tag{1}
$$

式(1)中$r(\pi)$为策略$\pi$下的独立于状态的平均奖励，$\tilde{v}_{\pi}(s)$为状态$s$的差值。对于ergodic MDPs，两者的定义为
$$
\begin{aligned}
r(\pi)\stackrel{\cdot}{=}\underset{n\to\infty}{lim}\frac{1}{n}\sum_{t=1}^n\mathbb{E}[R_t\vert S_0,A_{0:t-1}\sim\pi],~\tilde{v}_{\pi}(s)\stackrel{\cdot}{=}\mathbb{E}[\sum_{k=1}^{\infty}(R_{t+k}-r(\pi))\vert S_t=s,A_{t:\infty}\sim\pi]
\end{aligned}\tag{2}
$$
式中$e_{\pi}^{\gamma}(s)$表示误差项，在折扣因子$\gamma$趋近于$1$时接近于$0$。状态-动作价值的分解与状态的分解相似。

Laurent级数分解解释了奖励中心化有助于算法学习的原因。确切的说，动作的选择是基于相对价值，但是动作的价值估计需要独立的学习常数偏置。然而，若偏置过大，那么估计偏置的近似误差很容易mask动作之间的相对差。

在整个强化学习问题中，与状态无关的偏置是非常大。如图1所示，三状态的马尔可夫决策过程。状态$A$转换为状态$B$的奖励为$+3$，否则为$0$，平均奖励为$r(\pi)=1$。三个折扣因子下折扣状态价值可见下表。与标准折扣价值相比，中心化折扣价值随着折扣因子的增加，其变化幅度很小。同时，随着折扣因子接近于$1$，中心化折扣价值接近于差值。

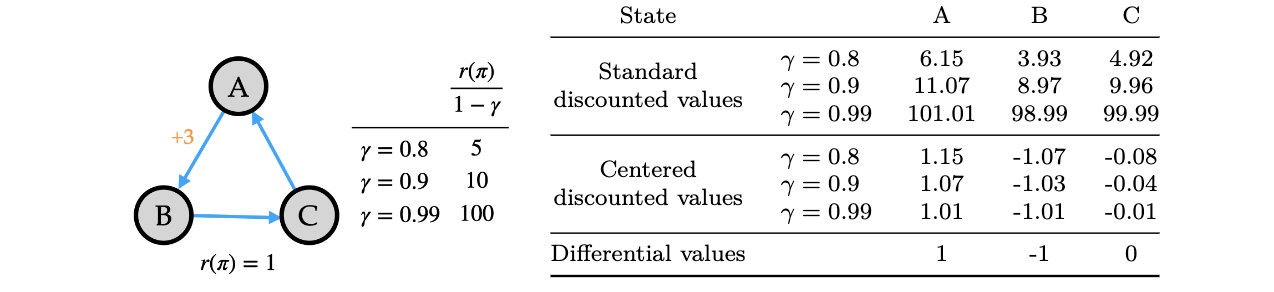
图1 标准折扣价值与中心化折扣价值在简单例子上的比较

正式的，中心化折扣价值为均值中心化的奖励折扣和的期望：
$$
\begin{aligned}
\tilde{v}_{\pi}^{\gamma}(s)=\mathbb{E}[\sum_{t=0}^{\infty}\gamma^t(R_{t+1}-r(\pi))\vert S_t=s,A_{t:\infty}\sim\pi],~v^{\gamma}_{\pi}(s)=\frac{r(\pi)}{1-\gamma}+\overbrace{\tilde{v}_{\pi}(s)+e_{\pi}^{\gamma}(s)}^{\tilde{v}_{\pi}^{\gamma}(s)},~\forall s
\end{aligned}\tag{3}
$$
式中$\gamma\in[0,1]$。若$\gamma=1$，那么中心化折扣价值与差值一致，即$\tilde{v}_{\pi}^{\gamma}(s)=\tilde{v}_{\pi}(s)$。通常情况下，中心化折扣价值为差值与误差项之和。

奖励中心化通过两个元件捕获折扣价值函数内的所有信息，分别是平均奖励常量和中心化折扣价值函数。这种分解的价值有：

• 随着$\gamma\to1$，折扣价值倾向于爆炸，而中心化折扣价值仍很小且可计算。
• 若问题的奖励偏移一个常数$c$，那么折扣价值的幅度增加$c/(1-\gamma)$，而中心化折扣价值不变，这是因为平均奖励也增加了一个$c$。

奖励中心化也使得算法设计中折扣因子在智能体学习期间可变。这是因为折扣因子的变化会导致标准折扣价值会发生很大的变化，而中心化价值的变化很小。

如图2所示，奖励中心化主要降低了样本复杂度，从而加快了学习效率。

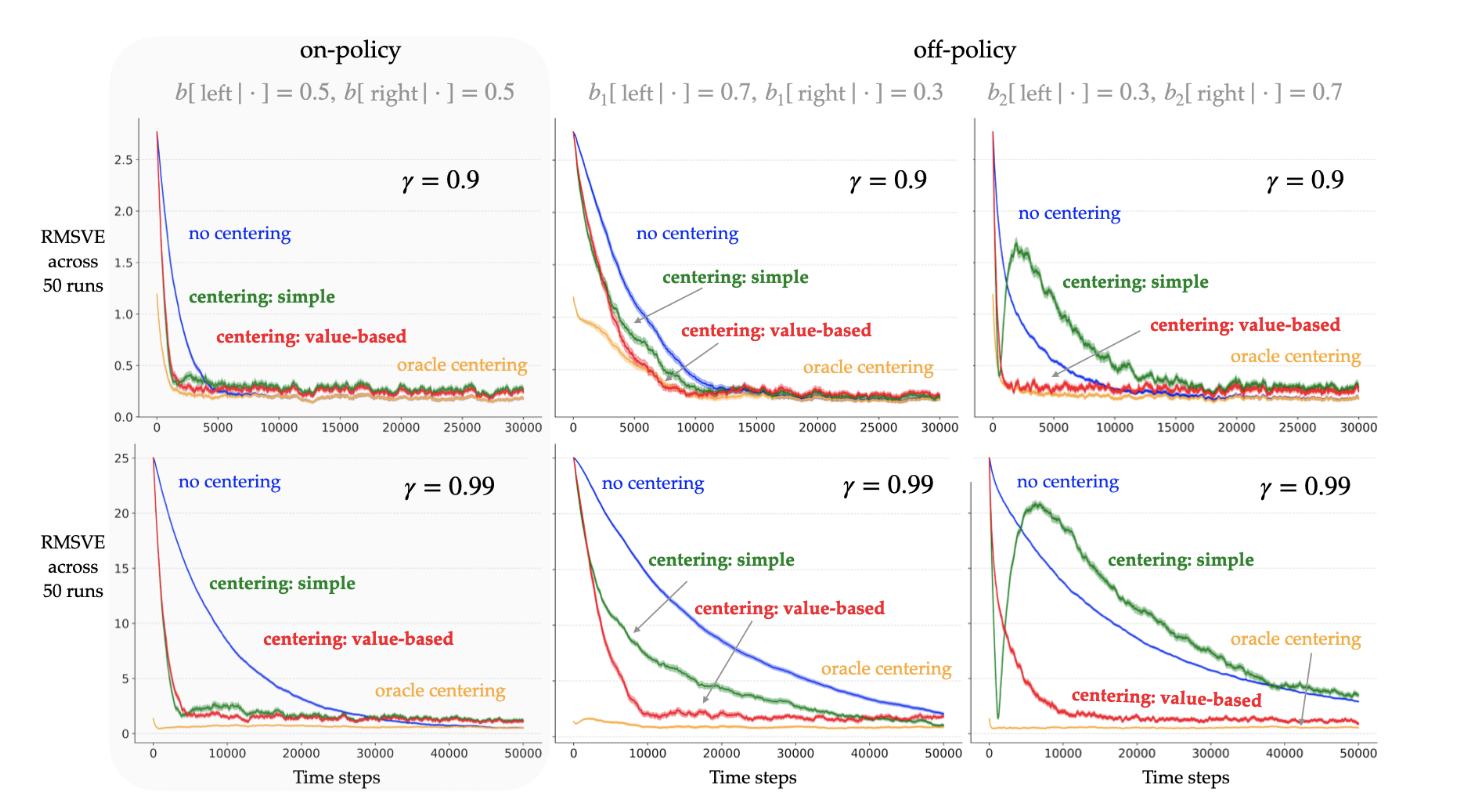
图2 表明奖励中心化对on-policy和off-policy影响的学习曲线

为了获得奖励中心化的益处，那么接下来介绍从数据中估计平均奖励的方法。

中心化方法

简单的奖励中心化

估计平均奖励最简单的方式是维护一个观测奖励的运行时平均。简单来说，若$t$时间步之后估计的平均奖励$\bar{R}_t=\sum_{k=1}^t R_k$，那么$t+1$步的平均奖励为
$$
\begin{aligned}
\bar{R}_{t+1}\stackrel{\cdot}{=}\bar{R}_t+\beta_t(R_{t+1}-\bar{R}_t)
\end{aligned}\tag{4}
$$
式中$\beta_t$为步长。这种更新方式属于平均奖励$\bar{R}_t\approx r(\pi)$的无偏估计。

若式(4)的中心化与时序差分相结合，那么价值函数$\tilde{V}^{\gamma}:\mathcal{S}\to\mathbb{R}$从$t$到$t+1$的转换为
$$
\begin{aligned}
\tilde{V}^{\gamma}_{t+1}(S_t)\stackrel{\cdot}{=}\tilde{V}_t^{\gamma}(S_t)+\alpha_t[(R_{t+1}-\bar{R}_t)+\gamma\tilde{V}_t^{\gamma}(S_{t+1})-\tilde{V}_t^{\gamma}(S_t)]
\end{aligned}\tag{5}
$$
且$\forall s\neq S_t$，那么$\tilde{V}_{t+1}^{\gamma}(s)\stackrel{\cdot}{=}\tilde{V}_t^{\gamma}(s)$

式中$\alpha_t\gt0$的步长参数。

局限性：然而，在Off-Policy场景中式(4)为行为策略$r(b)$平均奖励的无偏估计，而不是目标策略$r(\pi)$的。同时，重要性采样只是纠正动作分布的不匹配，而不是状态分布的不匹配，即重要性采样也不足以保证拟合到$r(\pi)$

基于价值的奖励中心化

论文Learning and Planning in Average-Reward Markov Decision Processes表明在表格型off-policy场景下，时序差分可为奖励率的无偏估计，即使在有折扣奖励范式下亦成立。若行为策略采取了目标策略所有的策略，那么平均奖励的近似为
$$
\begin{aligned}
\tilde{V}_{t+1}^{\gamma}(S_t)\stackrel{\cdot}{=}\tilde{V}_t^{\gamma}(S_t)+\alpha_t\rho_t\delta_t \\
\bar{R}_{t+1}\stackrel{\cdot}{=}\bar{R}_t+\eta+\alpha_t\rho_t\delta_t
\end{aligned}\tag{6}
$$
式中$\delta_t \stackrel{\cdot}{=}(R_{t+1}-\bar{R}_t)+\gamma\tilde{V}_t^{\gamma}(S_{t+1})-\tilde{V}_t^{\gamma}(S_t)$为时序差分，$\rho_t\stackrel{\cdot}{=}\pi(A_t\vert S_t)/b(A_t\vert S_t)$为重要项采样比例。由于这种中心化方式不仅包含奖励也包含价值，因此被称为基于价值的中心化。