扩散模型解决RL问题(一)

在解决控制任务时，RL呈现出样本效率低和模型表达能力有限的问题。为了提升RL的表达能力，一系列工作尝试把扩散模型与RL相结合。本篇文章主要介绍对于offline RL数据集，如何利用扩散模型解决RL问题，以及如何处理下游任务？

动作序列建模方法

MTDIFF利用扩散模型建模大规模多任务offline数据。确切的说，该方法利用基于Transformer的扩散模型和prompt learning进行生成式规划和数据合成。其中，生成式规划是指生成模型在给定条件下预测未来动作序列；数据合成是指在给定task-oriented提示下估计整个转换(包含状态、动作、以及奖励)的联合条件分布。实验中，发现，MTDIFF可以合成高质量的多任务数据，可进一步利用该数据进行增强offline数据集，从而提升策略表现。

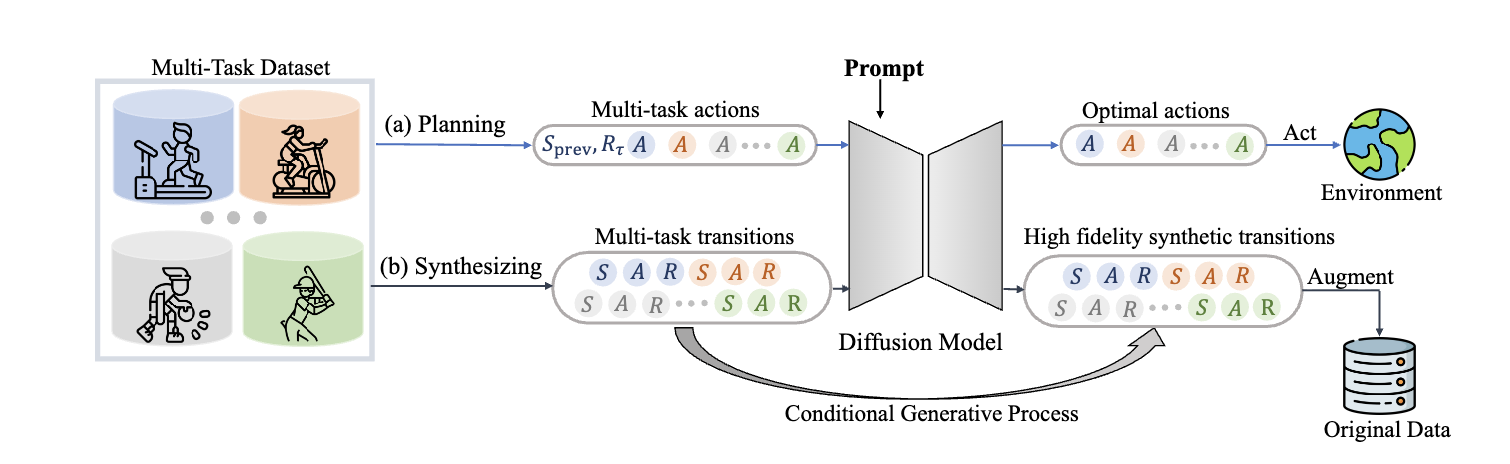
图1 MTDIFF整体网络架构

为了捕获从多个MDPs采样得到轨迹的多模态分布，把多任务轨迹建模为通过扩散模型的条件生成问题，即：
$$
\begin{aligned}
max_{\theta}\mathbb{E}_{\tau\sim\cup_i\mathcal{D}_i}[log p_{\theta}(x_0(\tau)\vert y(\tau))]
\end{aligned}\tag{1}
$$
式中$x_0(\tau)$为生成的期望序列，$y(\tau)$为条件。$x_0(\tau)$通过条件逆去噪过程$p_{\theta}$被用于生成式规划或数据合成。

Planning

在规划任务中，$x(\tau)$表示规划的动作序列，即
$$
\begin{aligned}
x_k^{p}(\tau):=(a_t,a_{t+1},\ldots,a_{t+H-1})_k
\end{aligned}\tag{2}
$$
上下文条件为
$$
\begin{aligned}
y^{p}(\tau):=[y^{'}(\tau),R(\tau)],~{y}'(\tau):=(Z,s_{t-L+1},\ldots,s_t)
\end{aligned}\tag{3}
$$
式中$t$为轨迹$\tau$的访问时刻$t$，$H$为输入序列的长度，$R(\tau)$为轨迹$\tau$下标准化累积回报，$L$为观测到的状态历史长度，$Z$为任务相关的信息作为prompt。同时，对于给定任务，$R(\tau)$作为classifier-free的引导以获得最优动作序列。

Data Synthesis

对于数据合成，输入输出变为了包含状态、动作、以及奖励的转换序列，即
$$
\begin{aligned}
x_k^{s}(\tau):=\begin{bmatrix}s_t & s_{t+1} & \cdots & s_{t+H-1}\\ a_t & a_{t+1} & \cdots & a_{t+H-1} \\ r_t & r_{t+1} & \cdots & r_{t+H-1}\end{bmatrix}
\end{aligned}\tag{4}
$$
条件为
$$
\begin{aligned}
y^{s}(\tau):=[Z]
\end{aligned}\tag{5}
$$

Prompt, Training and Sampling

在多任务场景，利用专家演示的轨迹片段以构建表达性提示。确切的说，任务标签$Z$作为轨迹提示，包含状态和动作
$$
\begin{aligned}
Z:=\begin{bmatrix}s_i^* & s_{i+1}^{*} & \cdots & s_{i+J-1}^{*} \\
a_i^{*} & a_{i+1}^{*} & \cdots & a_{i+J-1}^{*}
\end{bmatrix}
\end{aligned}\tag{6}
$$
式中$J$为识别任务的环境步数。以该提示为条件，MTDIFF可隐式的捕捉转换模型和奖励函数。

在规划任务中，通过classifier-free引导的方式进行动作规划。形式上，最优动作序列$x_0^p(T)$从高斯噪音$x_{K}(T)$开始采样，在逆扩散过程中，通过扰动噪音把$x_k^{p}(\tau)$变为$x_{k-1}^{p}(\tau)$。其中，扰动噪音为
$$
\begin{aligned}
\epsilon_{\theta}(x_k^p(\tau),{y}'(\tau),\varnothing,k)+\alpha(\epsilon_{\theta}(x_k^p(\tau),{y}'(\tau),R(\tau),k)-\epsilon_{\theta}(x_k^p(\tau),{y}'(\tau),\varnothing,k))
\end{aligned}\tag{7}
$$
式中$\alpha$为超参数，用于增强和抽取轨迹中带有高回报的部分。
在训练阶段，利用扩散模型DDPM和classifier-free引导的方式训练逆扩散过程，损失函数为
$$
\begin{aligned}
\mathcal{L}^p(\theta):=\mathbb{E}_{k\sim\mathcal{U}(1,K),x_0(\tau)\sim q,\epsilon\sim\mathcal{N}(0,1),\beta\sim Bern(p)}[\Vert\epsilon-\epsilon_{\theta}(x_k^{p}(k),{y}'(\tau),(1-\beta)R(\tau)+\beta\varnothing,k)\Vert^2]
\end{aligned}\tag{8}
$$
在推理阶段，采用low-temperature sampling技术产生高似然序列，即从$x_{k-1}^p(\tau)\sim\mathcal{N}(\mu_{\theta}(x_{k-1}^{p},{y}'(\tau),R_{max}(\tau),k-1),\beta\Sigma_{k-1})$，方差被$\beta\in[0,1]$缩放从而确保生成动作的最优性。

对于数据合成，其损失函数为
$$
\begin{aligned}
\mathcal{L}^{s}(\theta):=\mathbb{E}_{k\sim\mathcal{U}(1,K),x_0(\tau)\sim q,\epsilon\sim\mathcal{N}(0,I)}[\Vert\epsilon-\epsilon_{\theta}(x_{k}^s(\tau),{y}^{s}(\tau),k)\Vert^2]
\end{aligned}\tag{9}
$$
采样分布为$x_{k-1}^s(\tau)\sim\mathcal{N}(\mu_{\theta}(x_{k-1}^s,y^{s}(\tau),k-1),\Sigma_{k-1})$

状态动作序列建模方法

在人物控制领域，运动合成扩散模型可通过分类器引导在各种下游任务中重复使用，但物理一致性不足。与之不同，运动追踪策略预测动作的扩散模型无法重复使用，但物理一致性较强。
为了融合分类器引导和物理一致性能力，Diffuse-CLoC对于状态-动作进行联合扩散，使扩散模型成为自回归运动生成器和控制策略。

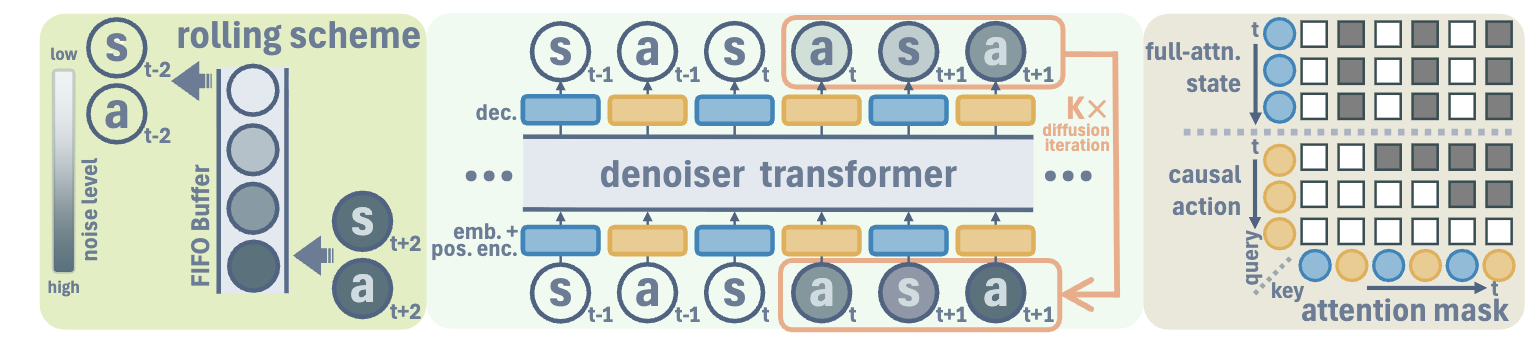
图2 Diffuse-CLoC网络架构

如图2所示，Diffuse-CLoC网络架构，其利用Transformer的Decoder进行建模。对于注意力机制，其动作利用因果注意力掩码只关注过去的状态，而状态不仅关注过去的状态也关注未来状态。然而，状态不关注动作，从而简化学习。同时，为了实现规划，预测未来$1s$的状态；为了确保预测动作的方差较低，预测未来$16$步的动作。

在策略推理阶段，利用receding horizon control的方式执行immediate动作。同时，为了避免规划轨迹不一致导致振荡，因此利用rolling inference scheme提升策略一致性。

总结

MTDIFF与Diffuse-CLoC均可用于多任务，只不过MTDIFF是classifier-free引导，而Diffuse-CLoC是classifier引导。这种方式不仅可处理offline-RL数据集，也可以对online RL策略进行蒸馏，例如：机器人领域通常先基于特权信息学习出teacher policy，然后再基于Dagger方式在部分观测下蒸馏出student policy。