扩散模型的可控生成与引导
Score-Based扩散模型中表明可利用训练中不可获得的信息调节生成过程。这是因为conditional reverse-time SDE可高效的从unconditional分数中估计。为了实现可控生成,通常需要进行引导。接下来,详细介绍该两部分内容。
可控生成的数学原理
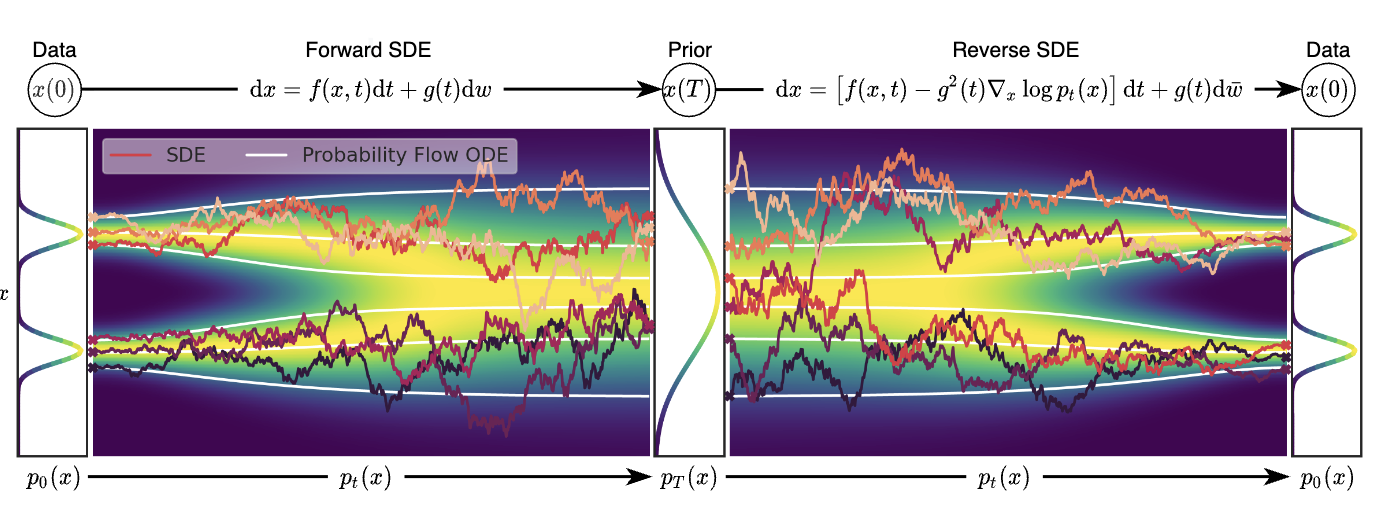
图1 score-based generative modeling through SDE概览
对于前向随机微分方程
$$
\begin{aligned}
d\mathbf{x}=\mathbf{f}(\mathbf{x},t)dt+g(t)d\mathbf{w}
\end{aligned}\tag{1}
$$
unconditional的逆随机微分方程为
$$
\begin{aligned}
d\mathbf{x}=[\mathbf{f}(\mathbf{x},t)-g(t)^2\nabla_{\mathbf{x}}logp_t(\mathbf{x})]dt+g(t)d\bar{\mathbf{w}}
\end{aligned}\tag{2}
$$
conditional的逆随机微分方程为
$$
\begin{aligned}
d\mathbf{x}=\{\mathbf{f}(\mathbf{x},t)-\nabla\cdot[\mathbf{G}(\mathbf{x},t)\mathbf{G}(\mathbf{x},t)^{T}]-\mathbf{G}(\mathbf{x},t)\mathbf{G}(\mathbf{x},t)^{T}\nabla_{\mathbf{x}}logp_{t}(\mathbf{x}\vert\mathbf{y})\}dt+\mathbf{G}(\mathbf{x},t)d\bar{\mathbf{w}}
\end{aligned}\tag{3}
$$
由于$p_t(\mathbf{x}(t)\vert \mathbf{y})\propto p_t(\mathbf{x}(t))p(\mathbf{y}\vert \mathbf{x}(t))$,那么分数$\nabla_{\mathbf{x}}logp_t(\mathbf{x}_t\vert \mathbf{y})$的计算方法为
$$
\begin{aligned}
\nabla_{\mathbf{x}}logp_t(\mathbf{x}(t)\vert\mathbf{y})=\nabla_{\mathbf{x}}logp_t(\mathbf{x}(t))+\nabla_{\mathbf{x}}logp(\mathbf{y}\vert\mathbf{x}(t))
\end{aligned}
$$
同时,由于$\mathbf{G}(\mathbf{x},t)=g(t)$,即散度$\nabla\cdot\mathbf{G}\mathbf{G}^{T}=0$
那么,式(3)可为
$$
\begin{aligned}
d\mathbf{x}=\{\mathbf{f}(\mathbf{x},t)-g(t)^2[\nabla_{\mathbf{x}}logp_t(\mathbf{x})+\nabla_{\mathbf{x}}logp_t(\mathbf{y}\vert\mathbf{x})]\}dt+g(t)d\bar{\mathbf{w}}
\end{aligned}\tag{4}
$$
根据式(3),可知,一旦获取到前向过程的梯度估计$\nabla_{\mathbf{x}}logp(\mathbf{y}\vert\mathbf{x}(t))$,那么可通过相应的采样器生成样本。
确切的说,$\nabla_{\mathbf{x}}logp_t(\mathbf{y}\vert\mathbf{x})$可通过训练模型进行估计,也可以通过启发式方法或领域知识进行估计。例如:在采样时,可以训练一个time-dependent分类器$p_t(\mathbf{y}\vert\mathbf{x}(t))$进行采样引导。
Guidance
可控生成分为两种,一种是分类器引导,另一种是Classifier-Free引导。其中,分类器引导是指训练一个分类器和分数估计模型,采样时混合分类器梯度和分数,从而引导采样。
为什么有Classifier-Free引导?
基于分类器的扩散采样可被解释为尝试利用基于梯度的对抗攻击confuse分类器,这种范式显然与GAN的训练相似。由此,猜测基于分类器引导的扩散模型是否在基于分类器的度量表现得很好?Classifier-Free引导的引入被用于回答该问题。
Classifier-Free引导的原理
简单来说,Classifier-Free引导混合了conditional扩散模型和unconditional扩散模型的分数估计,且两种扩散模型是联合训练的。该引导方式的训练和采样可见算法$1$和算法$2$

unconditional去噪扩散模型$p_{\theta}(\mathbf{z})$通过分数估计器$\epsilon_{\theta}(\mathbf{z}_{\lambda})$进行参数化,conditional去噪扩散模型$p_{\theta}(\mathbf{z}\vert\mathbf{c})$通过分数估计器$\epsilon_{\theta}(\mathbf{z}_{\lambda},\mathbf{c})$进行参数化。两个模型利用一个神经网络进行表达,即$\epsilon_{\theta}(\mathbf{z}_{\lambda})=\epsilon_{\theta}(\mathbf{z}_{\lambda},\mathbf{c}=\varnothing)$

在采样时,利用conditional和unconditional分数估计的线性组合作为分数估计
$$
\begin{aligned}
\tilde{\epsilon}_{\theta}(\mathbf{z}_{\lambda},\mathbf{c})=(1+w)\epsilon_{\theta}(\mathbf{z}_{\lambda},c)-w\epsilon_{\theta}(\mathbf{z}_{\lambda})
\end{aligned}\tag{5}
$$
由于$\tilde{\epsilon}_{\theta}$利用unconstrained神经网络估计的非保守向量场,那么通常不存在潜在的标量分类器,即该引导不属于基于梯度对抗攻击的分类器。
数学原理:
Classifier-Free引导受到隐式分类器梯度$p^{i}(\mathbf{c}\vert\mathbf{z}_{\lambda})\propto p(\mathbf{z}_{\lambda}\vert\mathbf{c})/p(\mathbf{z}_{\lambda})$的启发。若可得到确切的分数$\epsilon^{*}(\mathbf{z}_{\lambda},\mathbf{c})$和$\epsilon^{*}(\mathbf{z}_{\lambda})$,那么隐式分类器的梯度为$\nabla_{\mathbf{z}_{\lambda}}logp^{i}(\mathbf{c}\vert\mathbf{z}_{\lambda})=-\frac{1}{\sigma_{\lambda}}[\epsilon^{*}(\mathbf{z}_{\lambda},\mathbf{c})-\epsilon^{*}(\mathbf{z}_{\lambda})]$,且利用隐式分类器进行分类器引导可把分数估计改为
$$
\begin{aligned}
\tilde{\epsilon}^{*}(\mathbf{z}_{\lambda},\mathbf{c})=(1+w)\epsilon^{*}(\mathbf{z}_{\lambda},\mathbf{c})-w\epsilon^{*}(\mathbf{z}_{\lambda})
\end{aligned}\tag{6}
$$
式(6)与式(5)很相似,但不同。$\tilde{\epsilon}_{\theta}(\mathbf{z}_{\lambda},\mathbf{c})$为分数估计,而$\tilde{\epsilon}^{*}(\mathbf{z}_{\lambda},\mathbf{c})$为scaled分类器梯度。
最终,Classifier-Free引导与分类器引导的扩散模型拥有相似的性能。
引用方法
请参考:
li,wanye. "扩散模型的可控生成与引导". wyli'Blog (Sep 2025). https://www.robotech.ink/index.php/archives/769.html
或BibTex方式引用:
@online{eaiStar-769,
title={扩散模型的可控生成与引导},
author={li,wanye},
year={2025},
month={Sep},
url="https://www.robotech.ink/index.php/archives/769.html"
}