DTC：四足机器人可穿越稀疏奖励环境的深度轨迹追踪控制

足式运动是一个复杂的控制问题，它需要精确性和鲁棒性以应对真实世界的挑战。经典的方式是基于逆运动学的轨迹优化控制足式系统。这种层级的基于模型的方法很有吸引力，因为直观的成本函数、精确的规划、泛化性、以及数十年的研究成果积累。然而，模型的不匹配与假设的违反是错误产生的常见源头。另一方面，基于仿真的强化学习产生了空前的鲁棒性策略和恢复技能。尽管如此，所有的学习算法很难应对稀疏奖励的环境，在这样的环境中有效的足迹是稀疏的。DTC是一个混合控制架构，结合了经典的轨迹优化与基于学习的控制方式，同时实现更强的鲁棒性、足迹精确性、以及领域泛化性。具体来说，在训练阶段，基于模型的规划器产生参考运动。在仿真环境中训练深度神经网络以追踪参考运动的立足点。

引言

早期足式机器人运动的轨迹优化主要是运用简单的模型，例如刚体或倒立摆。这些方法需要机器人运行时的运动学和动力学，以及环境参数。后来，研究迁移到了更复杂的情形，例如：文献[2]中质心动力学或文献[3]中全身动力学。尽管这类方法产生了产生了敏捷的和多样的运动，但是由于不切实际的假设，使仿真与现实之间仍存在很大的间隔。

强化学习作为形成鲁棒性较强策略的一个强有力的工具，它不需要确定的模型。该方法是智能体与环境交互不断试错，从而得到一个闭环控制策略。虽然理论上基于强化学习方法可使机器人运动可以穿越稀疏奖励区域，但是需要好的探索策略。到目前为止，稀疏奖励区域只能被专门的策略所应对，且这种策略往往是对特定区域过拟合。

RL中的一些缺点可被基于优化的方法缓和。虽然稀疏奖励仍然存在，但是两个重要的优势可被采用：

• 成本函数和约束梯度可通过少量样本技术得到。
• 局部最优可被避免。

其中，避免局部最优的方法有：预先计算立足点([4],[5])、预先分割稀疏奖励区域([6],[7])、以及平滑整个奖励或梯度地图([8])。

在基于学习的社区，稀疏奖励或稀疏梯度问题已经被广泛的处理。一种方式是通过模仿专家行为学习特定任务，这类方式要么专家提供了演示以解决特定任务([9],[10])，要么被用于发现任务([11]-[13])。这种方式的可得到稠密的奖励函数。尽管如此，这种方式只是利用现有的知识降低样本复杂性和奖励复杂性。

为了进一步降低仿真与现实之间的间隔，文献[14]与[15]通过均匀采样立足点近似专家数据；文献[16]、[17]、以及[18]通过深度生成模型近似专家轨迹，从而得到更多的数据。然而，前者很难捕获真实基于模型控制器的分布，后者无法解决探索问题。

文献[1]中提出了基于轨迹优化引导探索的解决方案。由于这种数据线上与线下均可获得，所以被称为“参考”或专家运动。作者们也采用了文献[18]引入的层级结构。文献[18]中高层的规划器以低频率提出参考立足点，而底层控制器以高频跟随参考立足点。作者们并没有利用神经网络生成立足点，而是利用轨迹优化。此外，不仅仅利用目标立足点作为高层方向的指示器，也作为最优立足点的演示。

基于模型与无模型相结合的方法不是新的研究领域。例如：文献[19]中有监督学习和文献[20]、[21]中无监督学习的方式作为非线性求解器的冷启动。RL方法通过求解轨迹优化问题被用于模仿[9],[10]或纠正[22]轨迹优化得到运动策略。相反的，文献[17]基于模型的方法检测高层命令的可行性，文献[23]追踪学习的加速过程。与[22]相比，文献[1]并没有基于WBC学习纠正关节扭矩，而是学习参考轨迹到关节位置端到端的预测。

为了生成参考数据，文献[1]中作者们利用文献[8]中被称为领域意识的运动方法进行高效的轨迹优化。这种方式同时优化了立足点和基础姿势，因此能够使机器人以运动学极限运动。作者们只让策略得到解决方案子集的部分观测，这种方式相对于完全观测训练出来的策略鲁棒性更强。除此之外，通过使用可变的更新频率限制求解优化问题的计算成本。在部署时，优化器以尽可能快的速度运行，同时考虑模型的不确定性和外部的扰动性。

参考运动

设计控制器解决一个轨迹优化问题，总是存在精度与泛化性的妥协，以应对好的数值条件、低的计算时间、凸性、平滑性、可导性、以及高质量初始猜测的需要。在文献[1]中作者们采用文献[8]的TAMOLS方法生成轨迹。与别的相似方法不一样，它不需要领域分割，也不需要预先计算立足点，而且它对变化的初始猜测更有鲁棒性。

作者们也在TAMOLS增加了三个重要的特征：

• 允许使用CPU并行化，且可同时使用多种优化方法。
• 创建Python接口，从而允许在Python环境中运行。
• 假设测量的接触状态与期望的接触状态相吻合，从而使轨迹优化独立于接触估计。

优化器需要一个离散化2.5维度的环境模型表示作为输入，这种表示被称为高程图(elevation map)。简单来说，直接通过采样高度的方式从仿真器中抽取地图。

训练环境概览

运动策略$\pi(\mathbf{a}\vert\mathbf{o})$是动作$\mathbf{a}\in\mathcal{A}$以观测$\mathbf{o}\in\mathcal{O}$为条件的随机分布，被参数化为MLP。动作空间包括利用PD控制器追踪的目标关节位置。

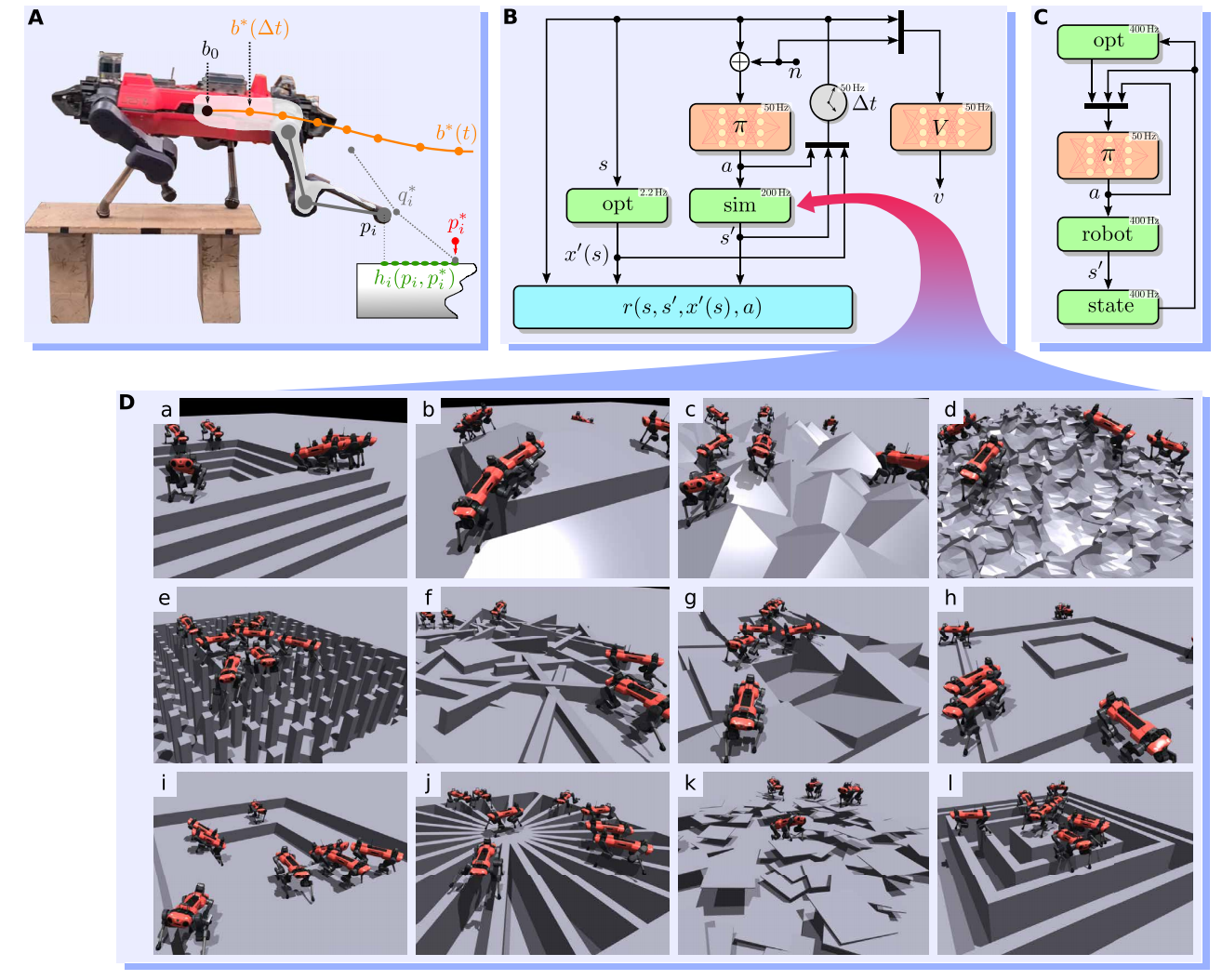
给定状态$\mathbf{s}\in\mathcal{S}$，从优化器中抽取下一个时间步的解决方案$\mathbf{x}'(s)\in\mathcal{X}\subseteq\mathcal{S}$，包含四个立足点$\mathbf{p}^{*}_{i=0,\ldots,3}$，触地时的关节位置$\mathbf{q}^*$，以及下一个时间步基座被估计的轨迹。该轨迹由基座位姿$\mathbf{b}^{*}(\Delta t)$，旋量$\dot{\mathbf{b}}^*(\Delta t)$，以及线性加速度和角加速度$\ddot{\mathbf{b}}^*(\Delta t)$，更多细节可见图1.A。然后，从策略中采样动作，被用于前向仿真系统动力学，产生新的状态${\mathbf{s}}'\in\mathcal{S}$，可见图1.B。

标量奖励函数被定为$r(\mathbf{s},{\mathbf{s}}',{\mathbf{x}}',\mathbf{a})$，是一个被优化的状态与测量的状态之间误差单调递减函数，也就是$r\propto{{\mathbf{x}}'(\mathbf{s})\ominus\mathbf{x}({\mathbf{s}}')}$。其中，减法运算$\ominus$被定义在集合$\mathcal{X}$上，向量${\mathbf{x}}'(\mathcal{s})$是被优化的状态，$\mathbf{x}({\mathbf{s}}')$为仿真起的状态。策略也可以被理解为一个参考自适应控制器建模的模型。

文献[1]中作者们基于异步的actor-critic方法在仿真环境中训练。利用特权观测$\tilde{o}\in\tilde{O}$和策略观测$o$作为近似价值函数$V(o,\tilde{o})$的输入。

观测空间

价值函数基于策略观测与特权观测训练获得，然而策略网络只是基于策略观测训练得到。所有的观测都是以机器人基座坐标系为中心的。接下来，对策略观测与特权观测进行介绍。

策略观测

策略观测包含本体感知度量，例如：基座旋量、重力向量、关节位置、以及关节速度。历史信息只有之前的动作。其它观测是从基于模型规划器中抽取得到的，包含立足点位置的平面坐标、期望触地时关节位置、期望接触状态、以及当前阶段剩下的时间。最后两个是每条腿各有一个，用于描述步态样式。立足点仅仅包含平面坐标，这是因为高度可以从高度扫描中抽取。

高度扫描是观测空间的另一部分，它使网络能够预测一个无碰撞的摆腿轨迹。与文献[17]相比，文献[1]没有构建一个稀疏的高程图。相反，只是沿着当下足的位置与期望立足点之间连线采样，可见图1.A。这种方式的优势为：

• 通过扫描与腿摆动最相关的区域进行采样可得到更稠密的高程图。
• 它阻止了网络抽取不相关的信息。
• 允许很方便为每条腿建模高程图漂移。

由于运动优化器不提供摆动轨迹，因此利用分析逆运动学计算期望的关节位置。同时，也不提供基座参考位姿作为观测，有助于降低对高程图误差的敏感性，也使策略独立于规划器。最后，为了允许网络推断期望行走方向，在观测空间增加参考旋量。

特权观测

特权观测包含提前抽取一个时间步由优化器产生的基座位姿、基座旋量、基座线加速度和角加速度。除此之外，critics还可以观测到仿真器提供的信号，例如：基座受到的外部力、足受到的外部力、测量到的外部接触力、摩擦系数、以及高程图漂移。

奖励函数

奖励函数由许多元件的权重和构成，包含的元件有参考运动追踪奖励、连续行为奖励、以及其它有助于sim-to-real的必要正则化项。

基座位姿追踪

为了实现参考基座位姿追踪，奖励为
$$
\begin{aligned}
r_{Bn}=e^{-\sigma_{Bn}\cdot\Vert\mathbf{b}^*(t+\Delta t)^{(n)}\ominus\mathbf{b}(t)^{(n)}\Vert^2}
\end{aligned}\tag{1}
$$
式(1)中$n=\{0,1,2\}$，$\mathbf{b}(t)$为测量的基座位姿，$\mathbf{b}^{*}(t+\Delta t)$为从参考轨迹中采样得到的期望基座位姿，$\ominus$表示基座方向的四元数差或者向量差。该奖励被视为“软”追踪任务，这是因为即使追踪误差没有完全消失仍可以得到大的奖励。

为了进一步分析，把基座的轨迹分成三个片段。“头”片段对应的时间索引为0，“尾”片段对应的时间索引为2，“中间”片段时间索引为1。指数形式奖励函数把追踪任务分为多阶段。在初始阶段，轨迹的追踪误差中部和尾部很可能相对大，因此将不会明显贡献奖励梯度，即会先最小化轨迹头的误差。一旦它在梯度上的效果消失，那么轨迹中间的误差将会占主导地位。在训练的最后阶段，追踪最可能提升轨迹尾部。

立足点追踪

立足点追踪的奖励函数
$$
\begin{aligned}
r_{pi}=-ln(\Vert\mathbf{p}^*_i-\mathbf{p}_i\Vert^2+\epsilon)
\end{aligned}\tag{2}
$$
式(2)中$\mathbf{p}_i$为腿的当前位置，$\mathbf{p}_i^*$为对应期望的立足点，且$0\lt\epsilon\lt1$，确保公式有意义。随着追踪的提升，奖励梯度将会变得更大，在后面训练阶段产生更“严格”的追踪。

一个稠密的奖励结构典型鼓励沿着地面拖着腿，从而最小化追踪误差。为了避免机器人拖着腿，在一个完整步态周期内只要腿受到力，那么智能体就收到至多一次奖励。

持续性

在足式运动的强化学习中，机器人犹豫在挑战领域运动是很常见的现象。这种现象阻止了更有信息的采样，也阻碍了机器人的表现。这种行为可被解释为不充分的探索：大部分智能体无法解决一个任务，而一小部分拒绝行走的智能体实现更高的平均奖励。为了解决这种局部最优，提出了鼓励行走的奖励。若两个连续的动作很相似，那么就被认为没有行走。这种相似是基于欧式距离度量的，可见式(3)
$$
\begin{aligned}
r_c=\sum_{\delta tj+t_0\in T(T_a\cap T_b)}-\delta t\Vert\mathbf{b}_a^*(\delta tj+t_{0,a})\ominus\mathbf{b}^*_b(\delta tj+t_{0,b})\Vert-w_p\Vert\mathbf{p}_a^*-\mathbf{p}_b^*\Vert
\end{aligned}\tag{3}
$$
式(3)中$\mathbf{p}^*_t$为栈中立足点，$t=\{a,b\}$，$\delta t=0.01$为基座轨迹的离散化时间，$t_0$为已经过去的时间。

正则化

为了确保机器人平滑的行走，利用两个不同的平滑项实施互补约束。第一项$r_{r1}=-\sum_i\vert v_i^Tf_i\vert$惩罚脚部受到的力避免脚的磨损和末端执行器的碰撞。第二项$r_{r2}=-\sum_i(\dot{\mathbf{q}}_i^T\tau_i)^2$惩罚关节功率以阻止任意的运动，特别是在摆动阶段。

模型训练与部署

观测和奖励函数设计完之后，就可以在仿真环境中训练策略。在训练策略时，作者们利用领域随机化和课程学习。在训练时，优化器的更新速度与脚的触底时间有关，以防止机器人产生“Lazy”行为。在部署时，优化器的更新频率尽可能的大。其中，轨迹优化器是完全基于真实数据进行训练而得到的。

参考文献

[1] Jenelten F, He J, Farshidian F, et al. DTC: Deep Tracking Control[J]. Science Robotics, 2024, 9(86): eadh5401.

[2] Grandia R, Jenelten F, Yang S, et al. Perceptive Locomotion Through Nonlinear Model-Predictive Control[J]. IEEE Transactions on Robotics, 2023.

[3] Mastalli C, Merkt W, Xin G, et al. Agile maneuvers in legged robots: a predictive control approach[J]. arXiv preprint arXiv:2203.07554, 2022.

[4] Jenelten F, Miki T, Vijayan A E, et al. Perceptive locomotion in rough terrain–online foothold optimization[J]. IEEE Robotics and Automation Letters, 2020, 5(4): 5370-5376.

[5] Mastalli C, Merkt W, Xin G, et al. Agile maneuvers in legged robots: a predictive control approach[J]. arXiv preprint arXiv:2203.07554, 2022.

[6] Grandia R, Jenelten F, Yang S, et al. Perceptive Locomotion Through Nonlinear Model-Predictive Control[J]. IEEE Transactions on Robotics, 2023.

[7] Griffin R J, Wiedebach G, McCrory S, et al. Footstep planning for autonomous walking over rough terrain[C]//2019 IEEE-RAS 19th international conference on humanoid robots (humanoids). IEEE, 2019: 9-16.

[8] Jenelten F, Grandia R, Farshidian F, et al. TAMOLS: Terrain-aware motion optimization for legged systems[J]. IEEE Transactions on Robotics, 2022, 38(6): 3395-3413.

[9] Brakel P, Bohez S, Hasenclever L, et al. Learning coordinated terrain-adaptive locomotion by imitating a centroidal dynamics planner[C]//2022 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2022: 10335-10342.

[10] Bogdanovic M, Khadiv M, Righetti L. Model-free reinforcement learning for robust locomotion using demonstrations from trajectory optimization[J]. Frontiers in Robotics and AI, 2022, 9: 854212.

[11] Peng X B, Abbeel P, Levine S, et al. Deepmimic: Example-guided deep reinforcement learning of physics-based character skills[J]. ACM Transactions On Graphics (TOG), 2018, 37(4): 1-14.

[12] Peng X B, Ma Z, Abbeel P, et al. Amp: Adversarial motion priors for stylized physics-based character control[J]. ACM Transactions on Graphics (ToG), 2021, 40(4): 1-20.

[13] Bohez S, Tunyasuvunakool S, Brakel P, et al. Imitate and repurpose: Learning reusable robot movement skills from human and animal behaviors[J]. arXiv preprint arXiv:2203.17138, 2022.

[14] Xie Z, Ling H Y, Kim N H, et al. Allsteps: curriculum‐driven learning of stepping stone skills[C]//Computer Graphics Forum. 2020, 39(8): 213-224.

[15] Duan H, Malik A, Dao J, et al. Sim-to-real learning of footstep-constrained bipedal dynamic walking[C]//2022 International Conference on Robotics and Automation (ICRA). IEEE, 2022: 10428-10434.

[16] Yu W, Jain D, Escontrela A, et al. Visual-locomotion: Learning to walk on complex terrains with vision[C]//5th Annual Conference on Robot Learning. 2021.

[17] Tsounis V, Alge M, Lee J, et al. Deepgait: Planning and control of quadrupedal gaits using deep reinforcement learning[J]. IEEE Robotics and Automation Letters, 2020, 5(2): 3699-3706.

[18] Peng X B, Berseth G, Yin K K, et al. Deeploco: Dynamic locomotion skills using hierarchical deep reinforcement learning[J]. ACM Transactions on Graphics (TOG), 2017, 36(4): 1-13.

[19] Melon O, Geisert M, Surovik D, et al. Reliable trajectories for dynamic quadrupeds using analytical costs and learned initializations[C]//2020 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2020: 1410-1416.

[20] Surovik D, Melon O, Geisert M, et al. Learning an expert skill-space for replanning dynamic quadruped locomotion over obstacles[C]//Conference on Robot Learning. PMLR, 2021: 1509-1518.

[21] Melon O, Orsolino R, Surovik D, et al. Receding-horizon perceptive trajectory optimization for dynamic legged locomotion with learned initialization[C]//2021 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2021: 9805-9811.

[22] Gangapurwala S, Geisert M, Orsolino R, et al. Rloc: Terrain-aware legged locomotion using reinforcement learning and optimal control[J]. IEEE Transactions on Robotics, 2022, 38(5): 2908-2927.

[23] Xie Z, Da X, Babich B, et al. Glide: Generalizable quadrupedal locomotion in diverse environments with a centroidal model[C]//International Workshop on the Algorithmic Foundations of Robotics. Cham: Springer International Publishing, 2022: 523-539.