Thinking-While-Moving：深度强化学习与并发控制

目前，强化学习算法聚焦的范式是：当智能体思考执行什么动作时，假设环境是静态的。然而，这种假设对于真实世界是不成立的，因为智能体在处理观测和规划下一步动作时，环境的状态也在不断的发生变化。对于这种不断变化的环境，被称为并发环境。为了能够基于深度强化学习处理并发环境，文献[1]提出了一个适用于并发马尔科夫决策过程的连续时间Bellman运算。同时，为了使并发环境下Q-Learning性能与同步环境下的性能相当，提出了状态观测可增加的最小信息量。

连续时间中的价值函数与策略

在并发环境中，利用微分方程定义连续时间的马尔科夫决策过程，可见式(1)
$$
\begin{aligned}
ds(t)=F(s(t),a(t))dt+G(s(t),a(t))d\beta
\end{aligned}\tag{1}
$$
式(1)中$\mathcal{S}=\mathbb{R}^d$为状态集合，$\mathcal{A}$为动作集合，$F:\mathcal{S}\times\mathcal{A}\to\mathcal{S}$与$G:\mathcal{S}\times\mathcal{A}\to\mathcal{S}$为描述环境随机动力学的函数，以及$\beta$是一个Wiener过程(具体可见文献[2])。

在连续时间场景下，$ds(t)$类似于离散时间中MDP的环境转移函数。连续时间函数$s(t)$与$a_i(t)$确定了状态和智能体采取的第$i$个动作。若智能体基于一个依赖于状态的确定性策略$\pi$与环境交互，那么轨迹$\tau=(s(t),a(t))$的回报可定义为
$$
\begin{aligned}
R(\tau)=\int_{t=0}^{\infty}\gamma^tr(s(t),a(t))dt
\end{aligned}\tag{2}
$$
价值函数为
$$
\begin{aligned}
V^{\pi}(s(t)) &= \mathbb{E}_{\tau\sim\pi}[R(\tau)\vert s(t)] \\
&= \mathbb{E}_{\tau\sim\pi}\int_{t=0}^{\infty}\gamma^tr(s(t),a(t))dt
\end{aligned}\tag{3}
$$
Q函数为
$$
\begin{aligned}
Q^{\pi}(s(t),a,t,H)=\mathbb{E}_{p}[\int_{{t}'=t}^{{t}'=t+H}\gamma^{{t}'-t}r(s({t}'),a({t}'))d{t}'+\gamma^HV^{\pi}(s(t+H))]
\end{aligned}\tag{4}
$$
式(4)中$H$为常数，代表的是轨迹的时长；$a$代表的是$t$至$t+H$时间段的连续动作函数；期望是关于式(1)中随机过程$p$计算的。

并发动作的马尔科夫决策过程

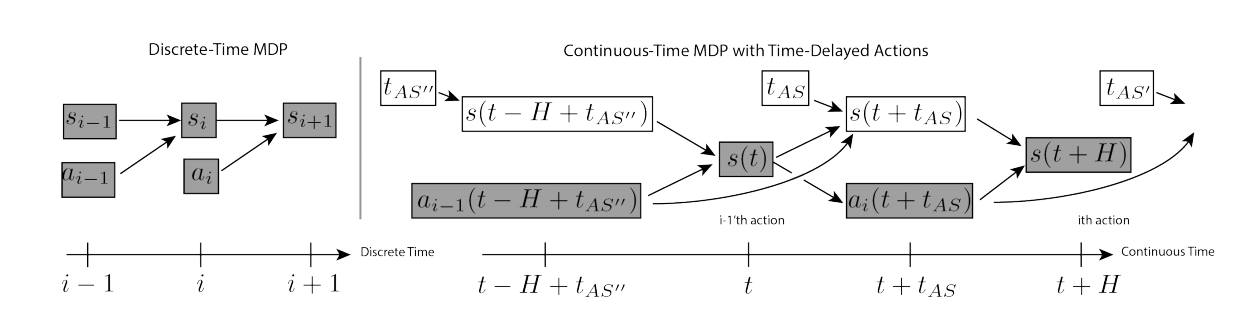
并发动作的MDP用于建模的场景是：智能体在执行之前动作同时，获取环境的状态。然后，根据状态选择合适的动作，无论之前的动作是否完成都要执行新动作，可见图2所示。在该场景下，并发动作可被视为沿着时间方向水平平移动作，其效果可见图1.b所示。

基于价值的并发强化学习算法

如何1.b所示，智能体在一个episode中选择$N$条动作轨迹，$a_1,\ldots,a_N$，每个$a_i(t)$为产生控制的连续函数。用$t_{AS}$表示捕获状态、策略推断、以及通信延时所需要的时间。在时刻$t$，智能体开始根据状态$s(t)$计算第$i$条轨迹$a_i(t)$，同时在$(t-H+t_{AS},t+t_{AS})$时间段内并发执行之前选择的轨迹$a_{i-1}(t)$。在时刻$t+t_{AS}$，智能体开始执行动作$a_i(t)$。那么，连续时间的$Q$函数被表达为

$$
\begin{aligned}
Q^{\pi}(s(t),a_{i-1},a_i,t,H)=\underset{Executing\quad action\quad trajectory\quad a_{i-1}(t)\quad until\quad t+t_{AS}}{\underbrace{\mathbb{E}_p[\int_{{t}'=t}^{{t}'=t+t_{AS}}\gamma^{{t}'-t}r(s({t}'),a_{i-1}({t}'))d{t}']}} \\+ \underset{Executing\quad action\quad trajectory\quad a_i(t)until\quad t+H}{\underbrace{\mathbb{E}_{p}[\int_{{t}'=t+t_{AS}}^{{t}'=t+H}\gamma^{{t}'-t}r(s({t}'),a_i({t}')d{t}')]}}+\underset{Value\quad function\quad at\quad t + H}{\underbrace{\mathbb{E}_p[\gamma^HV^{\pi}(s(t+H))]}}
\end{aligned}\tag{5}
$$

接下来，再定义并发贝尔曼运算

$$
\begin{aligned}
\tau^*_c\hat{Q}(s(t),a_{i-1},a_i,t,t_{AS})=\int_{{t}'=t}^{{t}'=t+t_{AS}}\gamma^{{t}'-t}r(s({t}'),a_{i-1}{t}'))d{t}'+ \\
\gamma^{t_{AS}}\underset{a_{i+1}}{max}\mathbb{E}_p\hat{Q}^{\pi}(s(t+t_{AS}),a_i,a_{i+1},t+t_{AS},H-t_{AS})
\end{aligned}\tag{6}
$$
文献[1]中作者们也证明了贝尔曼的收敛性。同时，也证明了并发离散时间的贝尔曼运算也是收敛的。

参考文献

[1] Xiao, T., Jang, E., Kalashnikov, D., Levine, S., Ibarz, J., Hausman, K., & Herzog, A. (2020). Thinking while moving: Deep reinforcement learning with concurrent control. arXiv preprint arXiv:2004.06089.

[2] https://en.wikipedia.org/wiki/Wiener_process