在线深度Actor-Critic算法的关键点

RL算法虽然概念上简单，但是许多SOTA算法实施使用了许多设计决策。然而，这些设计决策很少被讨论，就导致RL算法的进步很难被归因。Andrychowicz等人基于在线深度actor-critic框架进行了大规模试验，研究了这些设计对算法性能的影响。

研究这些设计对算法性能的影响，存在两个挑战：

• 性能优越的超参数很难配置。若算法的所有设计选择随机被采样，那么很可能造成训练效果差。
• 许多选择可能与别的相关选择有较强的相关性，例如：学习率与minibatch的大小。这些相关的选择就需要一切调节。

为了处理这些问题，Andrychowicz等人在做实验时，把许多有相关性的设计选择分到一组，即基于组的方式研究这些设计对性能影响。作者们研究了策略损失、网络架构、标准化与clipping、优势估计、训练设置、Timesteps处理、优化器、以及正则化对算法性能的影响。接下来，分别介绍一下这些设计选择及其影响，并给出相关建议。

实验结果

策略损失

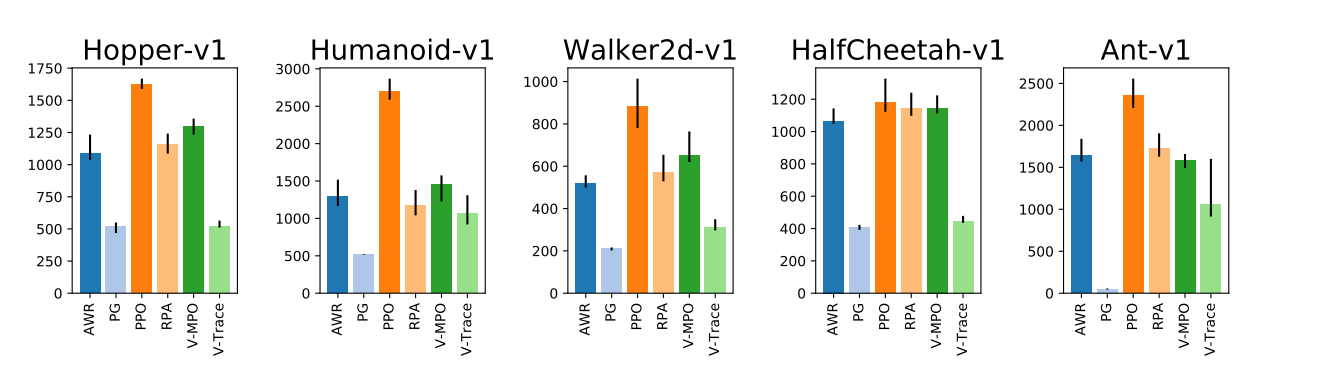
如图1所示，作者们研究了6中损失函数。实验结果表明，PPO算法的损失函数性能最好。然而，PG与V-trace的损失函数表现最差，这可能是因为它们无法处理一次迭代中变得偏离策略的数据，也有可能是经验的多次传递或与batch-size相比经验缓冲区较大的原因。总的来说，这些结果表明trust-region优化有利于降低样本复杂度。

建议： 利用PPO损失作为损失函数。clipping的阈值设定为$0.25$，也可尝试调大或调小。

网络架构

这一方面的研究主要关注网络架构、网络大小、激活函数、以及网络权重初始化对性能的影响。甚至，还包括动作函数标准差的选择与动作变形对算法性能的影响。其中，动作变形是指：在连续动作空间内，环境的动作是有界的，若基于高斯分布对其建模，那么就需要对神经网络的输出进行clip或使用tanh激活函数限制其输出范围。

结论：

• 对于大部分环境，策略网络与价值网络独立往往效果更好。
• MLP网络的最优宽度取决于环境的复杂性。
• 价值函数的MLP网络更宽不会对性能产生影响。
• 价值网络的宽度比策略网络的宽度更大，更有益处。
• 价值网络和策略网络有两个隐藏层就可以工作得很好。
• 对于MLP网络的激活函数，Tanh表现最好，Relu表现较差。

策略网络相关的结论：

• 初始策略似乎对算法性能影响很大。
• 策略网络初始化的关键点是：应使输出的动作分布与观测无关，以$0^{10}$为中心，且具有更小的标准差。对于策略与观测独立，可以通过以更小的权重初始化策略网络最后一层的方式实现。对于标准差，可通过引入一个常数偏置的方式控制标准差的初始化，例如：$$softplus(x)=log(e^x+1)$$。
• 根据图2可知，性能对动作初始标准差很敏感。

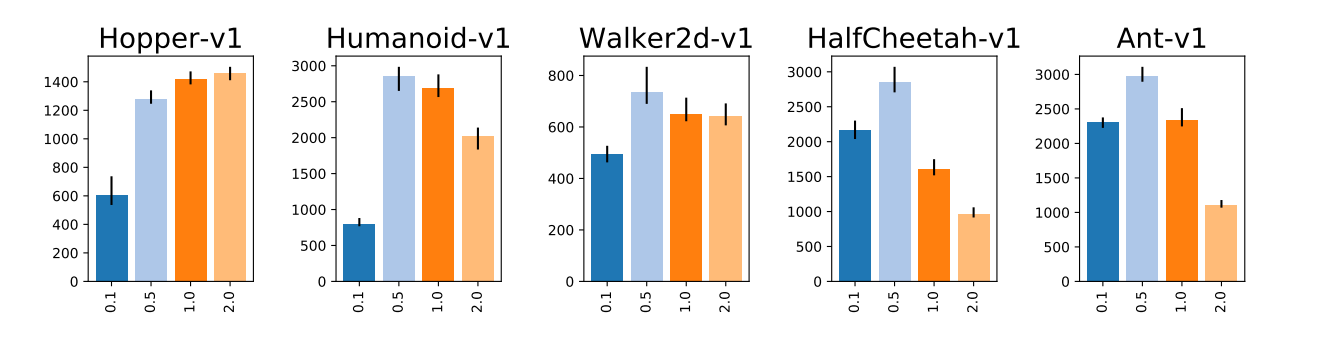
• 对于动作变形，研究结果发现，Tanh方式比Clipping表现好。这可能是因为tanh函数对最大可能策略熵的范围具有天然的限制有关。

其它结论：

• 价值网络最后一层初始化取值范围大小没有策略网络对性能影响大。
• 网络的初始化方式也不会带来太多的影响。
• 无论标准差是学出来的，还是固定的，对性能几乎无影响。
• 只要策略网络标准差不会太大，基本没影响。
• 策略网络标准差softplus与指数参数$e^x$化方式几乎对性能无影响。若基于指数参数遇到NaN的情况，clipping指数值会解决该问题。

建议： 基于100倍更小的权重初始化最后一层策略网络；使用softplus作为策略网标准差参数化方式；使用tanh作为激活函数和策略网络输出的变形；与策略网络相比，使用较宽的价值网络结构。

标准化与clipping

这一部分主要研究：观测标准化、价值函数标准化、per-minibatch优势标准化、以及梯度与观测的clipping对模型性能的影响。其中，观测标准化与价值函数标准化均是通过保存它们的均值和标准差，再计算得到。

结论：

• 对于大部分环境，观测标准化会使算法性能更优越。
• 有的环境价值函数标准化会提高性能，而其它的环境反而会降低性能。
• per-minibatch优势标准化似乎不会影响性能。
• clipping标准化后的观测对性能影响不大，但是它值得被运用以避免极端值的出现(仿真起发散)。
• 梯度clipping对性能提高有很小的帮助。

建议： 观测标准化一定要使用，检查价值函数标准化是否可提供性能。梯度裁剪作为次要的选项。

优势估计

这方面主要是研究：N-step、GAE、以及V-trace优势估计方法对性能的影响。

结论：

• GAE和V-trace优势估计的性能比N-steps优越，这说明结合多步价值估计有益处。
• GAE与V-trace之间没有发现明显的差别。
• $\lambda=0.9$时，GAE与V-trace均可表现的非常好。
• PPO中价值函数损失的clipping会伤害性能。
• 利用Huber损失，比MSE损失性能差。

建议： 利用$\lambda=0.9$下的GAE。

训练设置

这一部分主要研究数据收集和minibatch处理对性能的影响，主要包括并行化环境数量、每次迭代收集环境转换的数量、epochs的数量、minibatch大小以及数据被拆分成minibatch的方法。

对于数据拆分的方法，PPO的原始方式是：每次策略迭代把数据拆分成单个转换组合，然后随机分配到每个minibatch里面。这种方式打破了时序结构，使得计算优势不可能。因此，优势在每次策略迭代被计算一次，然后用于策略和价值函数优化。简单来说，这种方式是以使用旧的优势值作为代价增加每个minibatch数据的多样性。作为补救，作者们提出了每个epochs重新计算优势的方法。

结论：

• 经验多次回放对降低样本复杂度很重要。
• 随着并行环境数量的增加，一些环境下的算法性能极具下降。
• 并行环境的增加，有利于提高模型收敛速度。
• 增加batch-size大小，不会降低样本效率。
• 每次迭代收集的转换数大小对性能影响很大。
• 旧的优势值实际上会伤害性能，每个epoch重新计算它们会缓和该问题。

建议： 多次回放经验。每个epoch重新计算优势，且在把数据分配到minibatches之前进行shuffle。若要提高训练速度，增加并行环境的数量和batch-size的大小。同时，尽可能调节每次迭代中转换的数量。

Timesteps处理

这一部分主要是研究时间步相关的选择对模型性能的影响，包括折扣稀疏、跳帧数量、以及时间限制导致的episode终止。

结论：

• 算法性能严重依赖于折扣因子$\gamma$。若$\gamma=0.99$，对所有环境表现的很好。
• 跳帧只会提升大概$\frac{2}{5}$的环境。
• 时间步的限制导致episode遗弃，似乎不会影响性能，这当然有可能是作者设置的采样时间步过长导致的。

建议： 折扣因子$\gamma$是最重要的超参数，对每个环境应从$\gamma=0.99$开始调试。

优化器

这一部分主要研究了Adam与RMSprop优化器对模型性能的影响，还有优化器超参数和学习率线性衰退对性能的影响。

结论：

• 优化器对算法性能的影响似乎很小。
• 学习率对算法性能影响很大。其中，Adam算法学习率默认值$0.0003$在所有环境上表现均好。
• 学习率线性衰退至0会提高性能。

建议： 利用Adam作为优化器，其动量系数$\beta_1=0.9$、以及学习率为默认值。学习率线性衰退虽然能提升性能，但作为次要选项。

正则化

这一部分主要研究了策略的各种正则化器对算法性能的影响，要么是惩罚形式的正则化，或者软约束。其中，正则化项有：熵、标准正态策略与当前策略之间的KL-Divergence、当前策略与采样策略之间KL-Divergence和逆KL-Divergence。

结论： 对于几乎所有环境，正则化项均不会明显有助于性能的提升。这可能是因为PPO策略已经限制了策略更新的幅度，那么KL惩罚或约束属于冗余。同时，好的策略网络初始化已经足够保证好的探索。

            
                li,wanye. "在线深度Actor-Critic算法的关键点". wyli'Blog (Jan 2024). https://www.robotech.ink/index.php/archives/127.html            
        

            
                @online{eaiStar-127,

                   title={在线深度Actor-Critic算法的关键点},

                   author={li,wanye},

                   year={2024},

                   month={Jan},

                   url="https://www.robotech.ink/index.php/archives/127.html"

                }