基于RL的快速运动

在自然领域高速运动是很有挑战的，这是因为不同的领域需要机器人拥有不同的运动特性。若机器人尝试以更快的速度运行，那么领域变化对控制器性能的影响越来越大。解决这种问题一种可能的方式是设计精巧的模型和设计基于模型的控制器，即基于模型的控制(Model-Based Control, MBC)。然而，基于模型的控制器使机器人的行为和鲁棒性依赖于工程师的创新和大量时间的投入。同时，也需要设计控制尽可能简单以满足实时控制的要求。另外一种方式是基于完备的物理模型优化机器人动作，也即轨迹优化问题。由于完备物理模型的复杂性导致其几乎无法实时控制机器人。最后一种方法就是强化学习，这是一种基于学习的控制器，不需要精确的建模，智能体不断与环境交互使其自身累积奖励最大化，从而学习到鲁棒性较强的策略。

文献[1]的作者们构建了一个机器人以线速度和角速度取值范围较大的方式穿越自然领域的系统。由于每个线速度和角速度组合构建了一个独立任务，所以这种方式对应的是多任务强化学习范式。虽然之前线速度与角速度小范围取值的机器人学习取得了多任务策略学习的成功，但是增加速度范围使智能体反而学习不到信息。这可能是因为任务集中较难任务导致智能体不会收集到明显的奖励，从而导致无法得到有效的训练。

为了解决多任务强化学习这种特有的困难(来自于文献[2])，常见的方式是智能体先在简单的任务上学习，再缓慢的提高任务的复杂度，即课程学习。对于机器人系统，以往的工作是人工设计课程训练机器人。然而，面对任务的困难程度未知的情况时，人工设计的课程失效了。因此，文献[1]作者们提出了一种自动课程策略。总的来说，文献[1]作者们设计的学习系统有两个重要的模块，分别是自适应课程和线上系统识别。如图1所示，MIT Mini-Cheetah的学习效果。

图1第一行展示的是四足机器人能够在平坦地面上持续的以$3.9m/s$的速度运行；即使在不平坦的户外地面也能够以平均速度为$3.4m/s$跑$10m$，可见图1中第二行；在冰面上能够以$5.7rad/s$的方式运行，可见图1的第四行。文献[1]中作者们研究的机器人拥有最小的感知套装，主要有惯性测量单元陀螺仪和联合编码器。

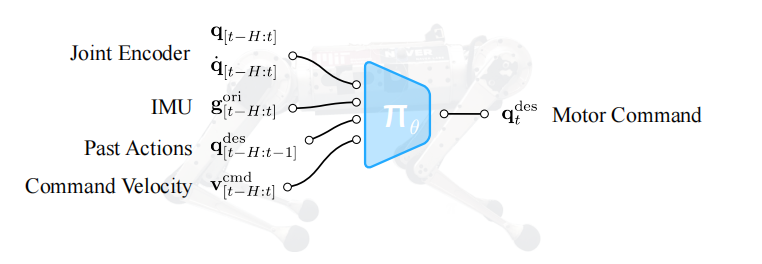
如图2所示，文献[1]作者们期望以传感器数据和速度命令为输入，然后输出关节位置命令。然后，关节位置命令被转化为关节扭矩。其中，速度命令$\mathbf{v}_t^{cmd}$包含纵向速度$\mathbf{v}_{x}^{cmd}$、横向速度$\mathbf{v}_x^{cmd}$、以及偏航率$\mathbf{w}_z^{cmd}$。

控制架构

观测空间： 关节角度$\mathbf{q}_t\in\mathbb{R}^{12}$和关节速度$\dot{\mathbf{q}}_t\in\mathbb{R}^{12}$是由电动机编码器提供的，以及机器人本体重力矢量的方向$\mathbf{g}_t^{ori}\in\mathbb{R}^3$由传感器IMU提供。策略$\pi_{\theta}(\cdot)$由历史观测和动作$\mathbf{o}_{t-H:t}$，以及速度命令$\mathbf{v}_t^{cmd}$为输入，用$\mathbf{x}_{t-H:t}$表示。其中，$\mathbf{x}_t=\mathbf{o}_t\oplus \mathbf{v}_t^{cmd}$，$\mathbf{o}_t=[\mathbf{q}_t,\dot{\mathbf{q}}_t,\mathbf{g}_t^{ori},\mathbf{a}_{t-1}]$。在部署期间，速度命令由人工远程控制确定。

奖励函数： 与文献[3]中奖励函数设计一致，由线速度和角速度追踪奖励和辅助奖励构成。其中，辅助奖励根据功能可划分为

• 稳定性：本体翻滚、仰俯、以及高度的惩罚。
• 平滑性：关节扭矩、加速度、以及动作变化程度的惩罚，还有关节摆动延时的奖励。
• 安全性：自我碰撞、关节限位越界的惩罚。

在具体实践中，作者们发现机器人在高速运行时倾向于下沉身体且向头部倾斜，因此引入了身体高度和旋向的惩罚。详细的奖励设置可见表示1所示。

对于动作空间，模型输出关节的位置，再输入到PD控制器。其中，PD控制器的比例增益大小设置的较小以使动作更平滑。

领域随机化

基于强化学习的策略往往是在仿真环境中训练，再迁移到真实环境。然而，由于真实环境未知，所以就需要Sim-to-Real的技术。其中，最常用的就是对系统动力学参数$\mathbf{d}_t$在一定范围内随机化配置，使智能体在不同的参数配置下学习，从而能够对真实环境具有更强的鲁棒性。

然而，领域随机化学习出的策略往往过于保守。若期望策略能够根据不同的环境选择不同的策略，那么一种方式就是线上系统识别。机器人能够识别出环境的动力学参数，然后再选择对应的策略$\pi_T(\mathbf{x}_t,\mathbf{d}_t)$。

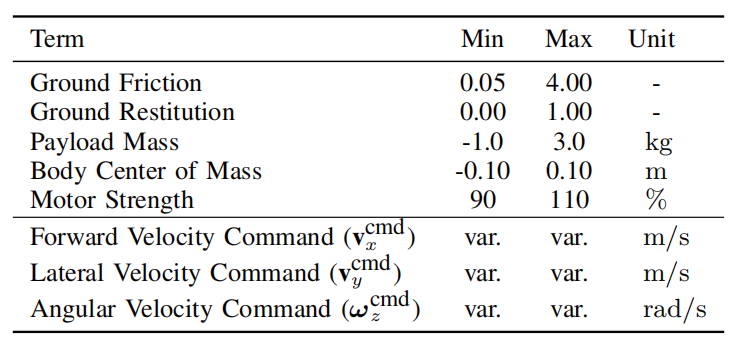
对于线上系统识别技术，智能体先根据由仿真环境提供的系统动力学参数进行策略学习。在部署时，通过监督学习以历史状态和速度指令为输入预测当前环境参数$\mathbf{d}_t$，即策略可表示为$\pi_S(\mathbf{x}_t,\mathbf{x}_{[t-h:t-1]})$。其中，参数的取值范围可见表2所示。

在具体实践中，策略学习分为两步，第一步是学习出Teacher Policy，第二步是学习出Student Policy。对于Teacher Policy策略学习有两个模块，一个模块是参数编码$\mathbf{z}_t=g_{\theta_d}(\mathbf{d}_t)$；另一个模块是预测策略$\mathbf{a}_t=\pi_{\theta_b}(\mathbf{x}_t,\mathbf{z}_t)$。同样，对于Student Policy策略学习也有两个模块，其中一个模块基于历史状态数据和速度指令数据预测Teacher Policy中对动力学参数的编码$\mathbf{z}_t$，即$\hat{\mathbf{z}}_t=h_{\theta_a}(\mathbf{x}_{[t-h:t-1]})$；另一个模块就是基于系统参数编码和状态为输入预测动作。

课程学习

直接以高速度为指令训练模型，导致智能体学习不到信息。因此，首先让机器人在简单环境和较低速度指令下学习，再逐级增加难度，从而使机器人能够应对真实复杂的环境。之前的研究是机器人基于固定的课程学习。然而，基于固定课程的学习失去了灵活性，若环境参数发生变化或学习算法改变，那么就需要重新修改课程。因此，文献[1]作者们提出了两种可以根据奖励和速度指令自适应的课程策略。

这两种课程策略分别是Box Adaptive Curriculum Update Rule和Grid Adaptive Curriculum Update Rule。在初始阶段，速度指令以$[-1.0,1.0]$为均匀分布。对于网络自适应课程，以$0.5rand/s$为分辨率定义网络。同时，作者们定义了成功阈值$0\lt\gamma\lt1$，以确定课程修改的时间。

Box Adaptive Curriculum Update Rule

这种方式的课程更新是把速度$\mathbf{v}_x^{cmd}$和$\mathbf{w}_z^{cmd}$分别视作独立的服从均匀分布。Box自适应课程更新规则可用式(1)和(2)表示。
$$
\begin{aligned}
p^{k+1}_{\mathbf{v}_x}(\mathbf{v}_x^n)\leftarrow\begin{cases}
p^k_{\mathbf{v}_x}(\mathbf{v}_x^n) & r_{v_x^{cmd}}\lt\gamma\\
1 & otherwise
\end{cases}
\end{aligned}\tag{1}
$$

$$
\begin{aligned}
p^{k+1}_{\mathbf{w}_z}(\mathbf{w}_z^n)\leftarrow\begin{cases}
p^k_{\mathbf{w}_z}(\mathbf{w}_z^n) & r_{w_z^{cmd}}\lt\gamma\\
1 & otherwise
\end{cases}
\end{aligned}\tag{2}
$$

式(1)和(2)中$r_{v_x^{cmd}},r_{w_z^{cmd}}$为追踪速度命令的奖励，$p$表示的课程学习中速度指令的分布。由于只根据$\mathbf{v}_x,\mathbf{w}_z$就可以确定全向运动，所以不考虑横向速度的自适应分布。

根据式(1),(2)，可知，若奖励超过$\gamma$，那么速度$\mathbf{v}_x$和$\mathbf{w}_z$以$0.5$为幅度进一步扩大采样范围，即$\mathbf{v}_x^{n}\in\{\mathbf{v}_x^{cmd}-0.5,\mathbf{v}_x^{cmd}+0.5\}$和$\mathbf{w}_z^{n}\in\{\mathbf{w}_z^{cmd}-0.5,\mathbf{w}_z^{cmd}+0.5\}$。

Grid Adaptive Curriculum Update Rule

这种方式的课程更新是把速度$\mathbf{v}_x^{cmd}$和$\mathbf{w}_z^{cmd}$视作服从联合均匀分布。Grid自适应课程更新规则可用式(3)表示。
$$
\begin{aligned}
p^{k+1}_{\mathbf{v}_x,\mathbf{w}_z}(\mathbf{v}_x^n,\mathbf{w}_z^n)\leftarrow\begin{cases}
p^k_{\mathbf{v}_x,\mathbf{w}_z}(\mathbf{v}_x^n,\mathbf{w}_z^n) & r_{v_x^{cmd}}\lt\gamma\quad or\quad r_{w_z^{cmd}}\lt\gamma\\
1 & otherwise
\end{cases}
\end{aligned}\tag{3}
$$
根据式(1)，可知，若速度$\mathbf{v}_x$和$\mathbf{w}_z$中一个奖励超过$\gamma$，那么对应的速度取值范围会以$0.5$为步长增加两个顶点。

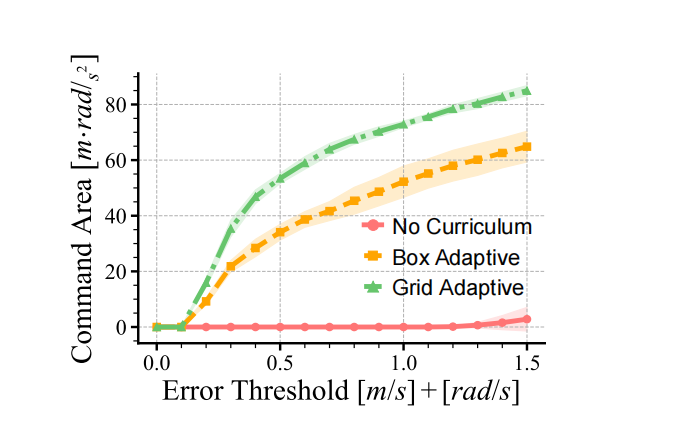
由于大多数高速无法得到有效训练，与Box自适应课程更新规则相比，这种方式能够使机器人展现出更多类型的步态，其实验结果比较可见图3所示。

参考文献

[1] Margolis G B, Yang G, Paigwar K, et al. Rapid locomotion via reinforcement learning[J]. arXiv preprint arXiv:2205.02824, 2022.

[2] Hessel, Matteo, et al. "Multi-task deep reinforcement learning with popart." Proceedings of the AAAI Conference on Artificial Intelligence. Vol. 33. No. 01. 2019.

[3] Rudin N, Hoeller D, Reist P, et al. Learning to walk in minutes using massively parallel deep reinforcement learning[C]//Conference on Robot Learning. PMLR, 2022: 91-100.