ACER：基于经验回放的样本高效的Actor-Critic算法

DQN算法利用经验回放奖励样本之间的相关性，很大的提高了算法的性能。经验回放实际上是一个提高样本效率强有力的工具。文献[1]中作者们提出了ACER(Actor Critic with Experience Replay)算法实现了与DQN相似甚至更高的性能，也优越于A3C。同时，ACER算法应该是首个可以同时应用于连续动作空间和离散动作空间的算法，主要的创新点有：带有偏差纠正的裁剪重要性采样、随机Dueling网络架构、以及高效可信区域策略优化。

与A3C一致，ACER也利用了多线程训练。与A3C不一致的是：ACER是一个off-policy学习算法，且利用了经验回放。接下来，分别在离散动作空间和连续动作空间详细介绍一下ACER的设计。

离散动作空间的ACER

基于经验回放的off-policy算法能够提升算法的样本效率。然而，控制off-policy算法的方差与偏差是很难。经常采用的技术是重要性采样。若基于行为策略$\mu$采样轨迹$\{x_0,a_0,r_0,\mu(\cdot\vert x_0),\cdots,x_k,a_k,r_k,\mu(\cdot\vert x_k)\}$，那么重要性权重策略梯度为
$$
\begin{aligned}
\hat{g}^{imp}=(\prod_{t=0}^k\rho_t)\sum_{t=0}^k(\sum_{i=0}^k\gamma^ir_{t+i})\nabla_{\theta}log\pi_{\theta}(a_t\vert x_t)
\end{aligned}\tag{1}
$$
式(1)中$\rho_t=\frac{\pi(a_t\vert x_t)}{\mu(a_t\vert x_t)}$表示重要性权重。由于重要性权重的乘积是无界的，所以该估计具有高的方差。若要直接对重要性权重进行裁剪，从而导致估计器的偏差增加。

文献[2]中作者们提出了一个极限分布的概念用于解决方差与偏差之间权衡的问题，可见式(2)
$$
\begin{aligned}
\hat{g}^{marg}=\mathbb{E}_{x_t\sim\beta,a_t\sim\mu}[\rho_t\nabla_{\theta}\pi_{\theta}(a_t\vert x_t)Q^{\pi}(x_t,a_t)]
\end{aligned}\tag{2}
$$
式(2)中$\mathbb{E}_{x_t\sim\beta,a_t\sim\mu}$是关于极限分布$\beta(x)=lim_{t\to\infty}P(x_t=x\vert x_0,\mu)$求期望。为了保持概念的简洁性，后文用$\mathbb{E}_{x_ta_t}[\cdot]$代替$\mathbb{E}_{x_t\sim\beta,a_t\sim\mu}[\cdot]$。基于极限分布，就不需要计算重要性权重的乘积，而是需要估计重要性权重$\rho_t$。

Q函数的多步估计

在ACER算法中，作者们利用文献[3]的Retrace算法估计$Q^{\pi}(x_t,a_t)$。基于行为策略$\mu$给定轨迹，那么Retrace估计器可被表示为
$$
\begin{aligned}
Q^{ret}(x_t,a_t)=r_t+\gamma\bar{\rho}_{t+1}[Q^{ret}(x_{t+1},a_{t+1})]+\gamma V(x_{t+1})
\end{aligned}\tag{3}
$$
式(3)中$\bar{\rho}_t=min\{c,\rho_t=\frac{\pi(a_t\vert x_t)}{\mu(a_t\vert x_t)}\}$表示裁剪的重要性权重。$Q$表示对$Q^{\pi}$的当下估计。

ACER算法利用Dueling网络架构，同时预测$Q_{\theta_v}(x_t,a_t)$和$\pi_{\theta}(a_t\vert x_t)$。其中，$Q$的估计是以基于回报的估计$Q^{ret}(x_t,a_t)$作为目标，损失函数的梯度为
$$
\begin{aligned}
(Q^{ret}(x_t,a_t)-Q_{\theta_v}(x_t,a_t))\nabla_{\theta_v}Q_{\theta_v}(x_t,a_t)
\end{aligned}\tag{4}
$$

带有偏差纠正的重要性权重裁剪

为了降低式(2)梯度计算的方差过大造成训练不稳定的风险，作者们引入了重要性权重截断和偏差纠正项，可见式(5)
$$
\begin{aligned}
g^{marg} &= \mathbb{E}_{x_ta_t}[\rho_t\nabla_{\theta}log{\pi_{\theta}}(a _t\vert x_t)Q^{\pi}(x_t,a_t)] \\
&=\mathbb{E}_{x_t}[\mathbb{E}_{a_t}[\bar{\rho}_t\nabla_{\theta}log\pi_{\theta}(a_t\vert x_t)Q^{\pi}(x_t,a_t)]+\underset{a\sim\pi}{\mathbb{E}}([\frac{\rho_{t}(a)-c}{\rho_{t}(a)}]_{+}\nabla_{\theta}log\pi_{\theta}(a\vert x_t)Q^{\pi}(x_t,a))]
\end{aligned}\tag{5}
$$
式(5)中第一项为重要性权重截断项以降低方差，而第二项为偏差纠正项。偏差纠正项表明只有方差足够大时，才会得到纠正。

若利用$Q_{\theta_v}(x_t,a_t)$对$Q^{\pi}(x_t,a)$建模，那么
$$
\begin{aligned}
g^{marg}=\mathbb{E}_{x_t}[\mathbb{E}_{a_t}[\bar{\rho}_t\nabla_{\theta}log\pi_{\theta}(a_t\vert x_t)Q^{ret}(x_t,a_t)]+\underset{a\sim\pi}{\mathbb{E}}([\frac{\rho_{t}(a)-c}{\rho_{t}(a)}]_{+}\nabla_{\theta}log\pi_{\theta}(a\vert x_t)Q_{\theta_v}(x_t,a))]
\end{aligned}\tag{6}
$$
式(6)中包含一个MDP的静态分布。若给定轨迹$\{x_0,a_0,r_0,\mu(\cdot\vert x_0),\cdots,x_k,a_k,r_k,\mu(\cdot\vert x_k)\}$，那么式(6)为
$$
\begin{aligned}
g^{marg}=\bar{\rho}_t\nabla_{\theta}log\pi_{\theta}(a_t\vert x_t)[Q^{ret}(x_t,a_t)-V_{\theta_v}(x_t)]+ \\
\underset{a\sim\pi}{\mathbb{E}}([\frac{\rho_{t}(a)-c}{\rho_{t}(a)}]_{+}\nabla_{\theta}log\pi_{\theta}(a\vert x_t)[Q_{\theta_v}(x_t,a)-V_{\theta_v}(x_t)])
\end{aligned}\tag{7}
$$

高效的可信区域策略优化

与TRPO一致，为了稳定训练，对策略网络的更新幅度进行了限制。由于TRPO的限制方法产生很大的计算开销，ACER算法提出了一种新的限制方法。

作者们把策略网络分成了两个部分，分别是分布$f$和深度神经网络输出的分布$\phi_{\theta}(x)$，策略被表示为$\phi_{\theta}:\pi(\cdot\vert x)=f(\cdot\vert\phi_{\theta}(x))$。那么，策略的梯度为
$$
\begin{aligned}
g^{acer}_t=\bar{\rho}_t\nabla_{\phi_{\theta}(x_t)}logf(a_t\vert\phi_{\theta}(x))[Q^{ret}(x_t,a_t)-V_{\theta_v}(x_t)]+ \\
\underset{a\sim\pi}{\mathbb{E}}([\frac{\rho_{t}(a)-c}{\rho_{t}(a)}]_{+}\nabla_{\phi_{\theta}(x_t)}logf(a_t\vert\phi_{\theta}(x))[Q_{\theta_v}(x_t,a)-V_{\theta_v}(x_t)])
\end{aligned}\tag{8}
$$
根据式(8)，可知，策略梯度是对策略网络输出的梯度，而不是策略网络的参数，这种分开是刻意的。

策略网络的更新，分为两步，第一步求解如下优化问题
$$
\begin{aligned}
& \underset{z}{minimize} \quad \frac{1}{2}\Vert\hat{g}_t^{acer}-z\Vert_2^2 \\
& subject\quad to\quad \nabla_{\phi_{\theta}(x_t)}D_{KL}[f(\cdot\vert\phi_{\theta_a}(x_t)\Vert f(\cdot\vert\phi_{\theta}(x_t)))]
\end{aligned}\tag{9}
$$
式(9)的优化问题，可直接利用KKT条件求解。若$k=\nabla_{\phi_{\theta}(x_t)}D_{KL}[f(\cdot\vert\phi_{\theta_a}(x_t))\Vert f(\cdot\vert\phi_{\theta}(x_t))]$，那么优化问题的解可被表示为
$$
\begin{aligned}
z^{*}=\hat{g}^{acer}-max\{0,\frac{k^T\hat{g}_t^{acer}-\delta}{\Vert k \Vert_2^2}\}k
\end{aligned}\tag{10}
$$
这表明，若满足上述优化问题的约束，那么策略对$\phi_{\theta}(x_t)$的梯度不发生改变。否则，更新的幅度会降低。接下来，在第二个阶段，就是基于反向传播算法更新网络参数。参数更新的大小与幅度为$\frac{\partial\phi_{\theta}(x)}{\partial\theta}z^*$。值得一提的是，trust region step的大小是在分布$f$统计得到的，而不是策略参数的空间。如图1所示，ACER在离散动作空间的算法伪代码。

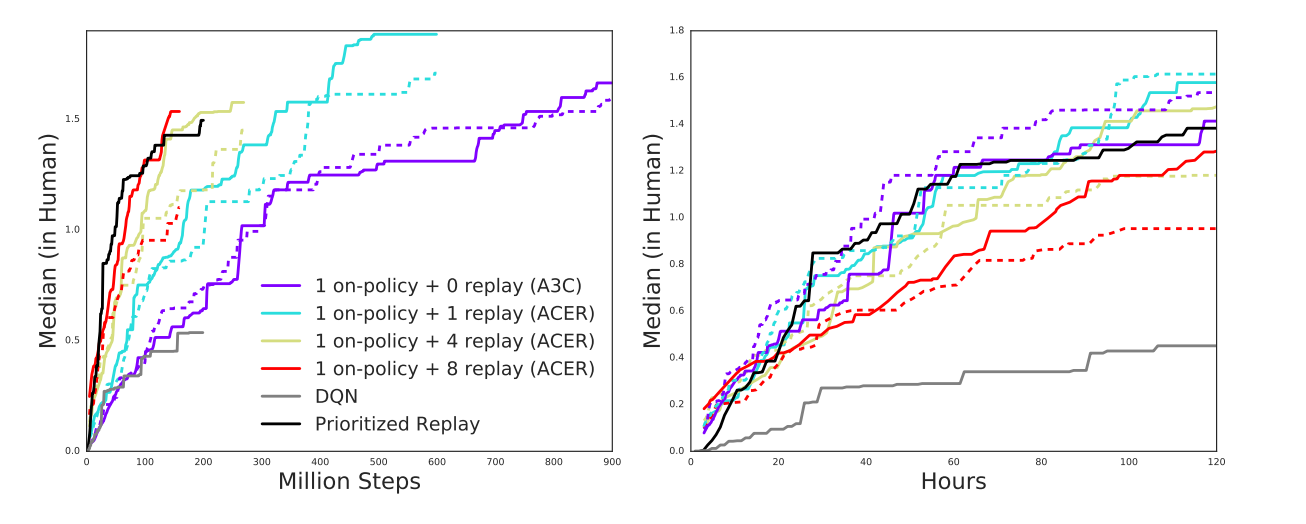
如图2所示，ACER算法在Atari游戏中的效果，可以了解到有较高样本效率和较好模型效果。

连续动作空间的ACER

对于连续动作空间无法从$Q$函数直接推导出$V$，但是Retrace算法对这两个函数都需要进行估计。因此，作者提出了强化学习的一个新的表示形式以解决该问题。

策略估计

作者们受到Dueling网络的启发，设计随机Dueling网络，可见图3所示。该网络同时估计off-policy的$V^{\pi}$与$Q^{\pi}$。为了保持$V^{\pi}$与$Q^{\pi}$的一致性，SDN网络的输出满足
$$
\begin{aligned}
\tilde{Q}_{\theta_v}(x_t,a_t)\sim V_{\theta_v}(x_t)+A_{\theta_v}(x_t,a_t)-\frac{1}{n}\sum_{i=1}^{n}A_{\theta_v}(x_t,v_i)
\end{aligned}\tag{11}
$$
其中，$\mu_i\sim\pi_{\theta}(\cdot\vert x_t)$。$Q^{\pi}$函数与$V^{\pi}$函数保持一致，意味着$\mathbb{E}_{a\sim\pi(\cdot\vert x_t)}[\mathbb{E}_{\mu_{1:n}\sim\pi(\cdot\vert x_t)}(\tilde{Q}_{\theta_v}(x_t,a))]=V_{\theta_v}(x_t)$。

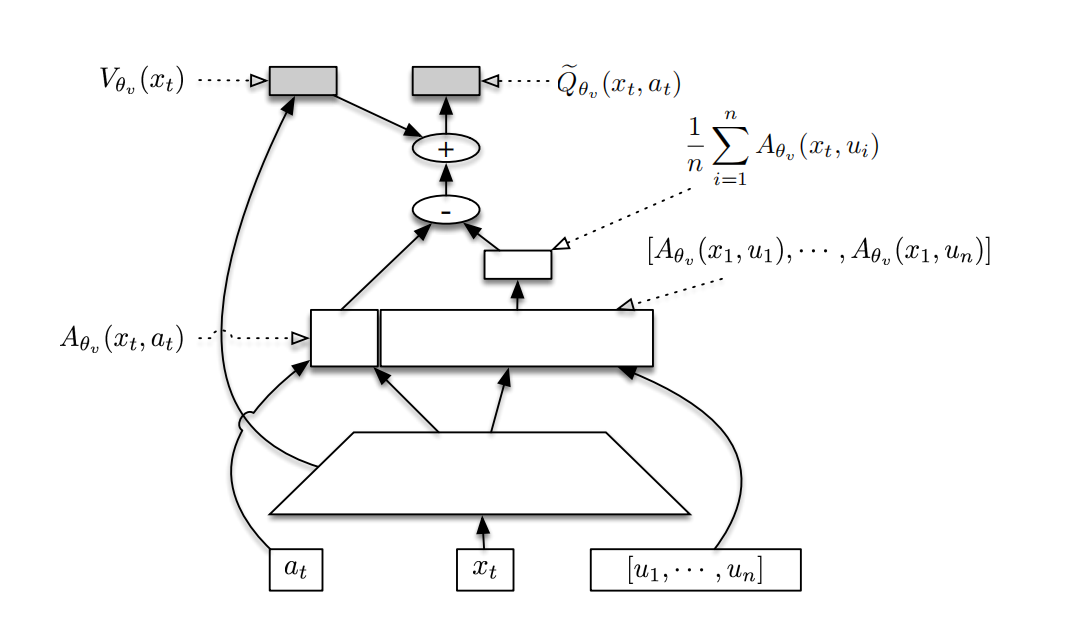
若$\mathbb{E}_{\mu_{1:n}\sim\pi(\cdot\vert x_t)}(\tilde{Q}_{\theta_v}(x_t,a_t))=Q^{\pi}(x_t,a_t)$，那么$V_{\theta_v}(x_t)=\mathbb{E}_{a\sim\pi(\cdot\vert x_t)}[\mathbb{E}_{\mu_{1:n}\sim\pi(\cdot\vert x_t)}(\tilde{Q}_{\theta_v}(x_t,a))]=\mathbb{E}_{a\sim\pi(\cdot\vert x_t)}[Q^{\pi}(x_t,a)]=V^{\pi}(x_t)$。由此可知，$\tilde{Q}_{\theta_v}(x_t,a_t)$也能够为$V_{\theta_v}$提供误差信号。

因此，为了估计$V^{\pi}$设计了新的目标
$$
\begin{aligned}
V^{target}(x_t)=min\{1,\frac{\pi(a_t\vert x_t)}{\mu(a_t\vert x_t)}\}(Q^{ret}(x_t,a_t)-Q_{\theta_v}(x_t,a_t))+V_{\theta_v}(x_t)
\end{aligned}\tag{12}
$$
文献[1]中也对式(12)进行了详细的推导证明。

最后，对于估计$Q^{ret}$采用了与离散动作空间不同的重要性权重裁剪，即$\bar{\rho}_t=min\{1,(\frac{\pi(a_t\vert x_t)}{\mu{a_t\vert x_t}})^{\frac{1}{d}}\}$。其中，$d$为动作空间的维度。

可信区域更新

与离散动作空间一致，也把策略的更新分为了两步。其中，分布$f$的选择为协方差矩阵固定和均有由策略网络$\phi_{\theta}(x)$预测的高斯分布。那么，策略的梯度为
$$
\begin{aligned}
g^{acer}=\mathbb{E}_{x_t}[\mathbb{E}_{a_t}[\bar{\rho}_t\nabla_{\phi_{\theta}(x_t)}logf(a_t\vert\phi_{\theta}(x_t))(Q^{opc}(x_t,a_t)-V_{\theta_v}(x_t))] \\
+\underset{a\sim\pi}{\mathbb{E}}([\frac{\rho_t(a)-c}{\rho_t(a)}]_{+}(\tilde{Q}_{\theta_v}(x_t,a)-V_{\theta_v}(x_t))\nabla_{\phi_{\theta}(x_t)}logf(a\vert\phi_{\theta}(x_t)))]
\end{aligned}\tag{13}
$$
式(13)中$Q^{opc}(x_t,a_t)$除了重要性权重裁剪率替换为1外，其它均与文献[3]的一致。如图4所示，ACER算法在连续动作空间的伪代码。

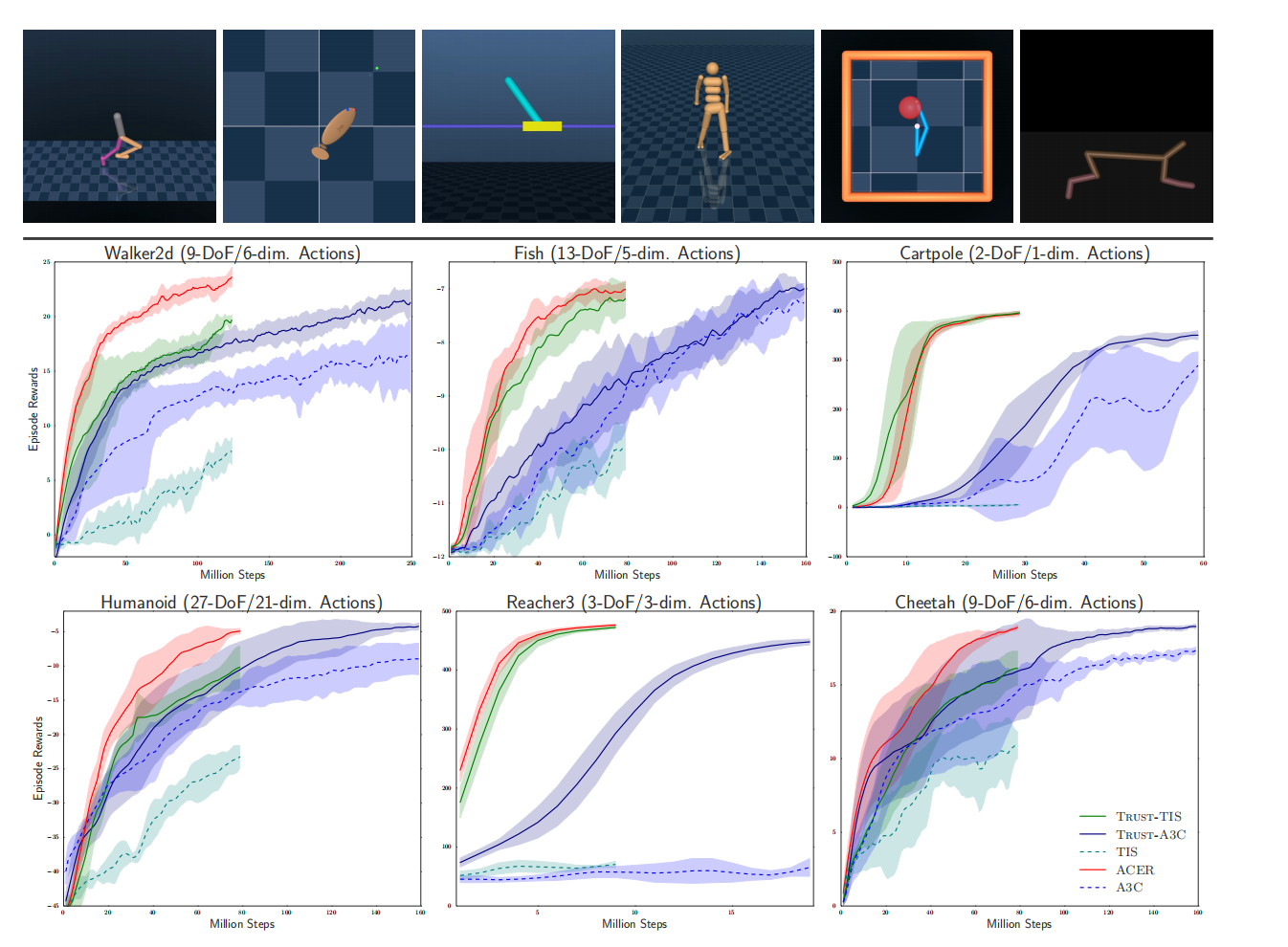
如图5所示，ACER算法在连续动作空间的表现。

参考文献

[1] Wang Z, Bapst V, Heess N, et al. Sample efficient actor-critic with experience replay[J]. arXiv preprint arXiv:1611.01224, 2016.

[2] Degris T, White M, Sutton R S. Off-policy actor-critic[J]. arXiv preprint arXiv:1205.4839, 2012.

[3] Munos R, Stepleton T, Harutyunyan A, et al. Safe and efficient off-policy reinforcement learning[J]. Advances in neural information processing systems, 2016, 29.