基于不确定估计的方法与REM算法

基于不确定性估计的离线强化学习方法允许策略在保守型离线策略与离线策略之间转换。也可以这样理解，若函数近似的不确定性被评估，那么低不确定性区域策略的约束可被松弛。其中，不确定性的估计可以是策略、价值函数、或模型；不确定性估计的可用度量有方差、标准差等。

以估计$Q$函数不确定性为例，若$\mathcal{P}_{\mathcal{D}}(Q^{\pi})$表示$Q$函数关于数据集$\mathcal{D}$的分布，那么策略梯度的目标函数可写为
$$
\begin{aligned}
J(\theta)=\mathbb{E}_{s,a\sim\mathcal{D}}[\mathbb{E}_{Q^{\pi}\sim\mathcal{P}_{\mathcal{D}(.)}}[Q^{\pi}(s,a)-\alpha U_{\mathcal{P}_{\mathcal{D}}}(\mathcal{P}_{\mathcal{D}}(.))]]
\end{aligned}\tag{1}
$$
式(1)中$U_{\mathcal{P}_{\mathcal{D}}}(.)$为Q函数分布$\mathcal{P}_{\mathcal{D}}(.)$的度量，即增加了一个不确定性的惩罚项。

Random Ensemble Mixture

REM作者们利用方差度量Q函数不确定性进行了直接的尝试。该文章主要有三个贡献，分别是

• 一份由DQN智能体在Atari-2600的每个游戏中交互5千万次数据集被提供，用于评估离线强化学习算法。
• 经过研究，发现，离线QR-DQN[4]算法性能比数据集中表现最好的DQN智能体还好。该结果与之前研究的不一致，可能是离线数据集大小、以及离线强化学习算法不一致的原因。
• 一个robust Q-learning算法REM被提出。在离线场景下，该算法表现出较强的泛化性，且性能超过离线QR-DQN。

Robust Offline Q-learning

在监督学习中，集成是一种提升模型泛化性常用的方法。文献[3]研究了两种算法，分别是Ensemble DQN与REM。

Ensemble DQN

通俗来讲，$K$个不同参数初始化的$DQN$，利用同一批次的数据学习，其损失函数为
$$
\begin{aligned}
\mathcal{L}(\theta)=\frac{1}{K}\sum_{k=1}^K\mathbb{E}_{s,a,r,{s}'\sim\mathcal{D}}[\mathcal{l}_{\lambda}(\Delta_{\theta}^k(s,a,r,{s}'))] \\
\Delta_{\theta}^k(s,a,r,{s}')=Q_{\theta}^k(s,a)-r-\gamma\underset{{a}'}{max}Q^k_{{\theta}'}({s}',{a}')
\end{aligned}\tag{2}
$$
式(2)中$l_{\lambda}$为Huber损失，可见式(3)
$$
\begin{aligned}
l_{\lambda}(u)=\begin{cases}
\frac{1}{2}u^2,if\vert u\vert\le\lambda\\
\lambda(\vert u\vert-\frac{1}{2}\lambda),otherwise
\end{cases}
\end{aligned}\tag{3}
$$

REM

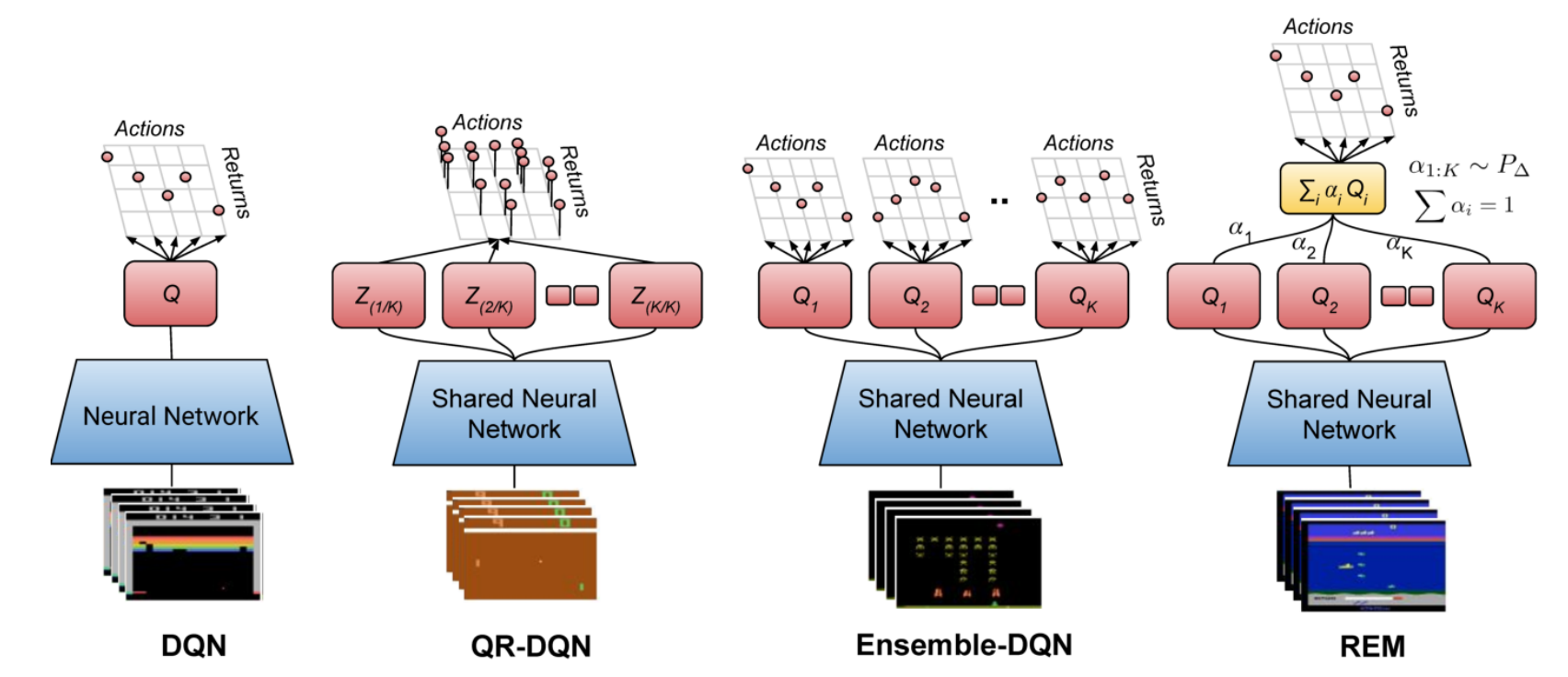
图1 DQN,QR-DQN,Ensemble-DQN,REM网络架构

REM算法背后的思想是以一种计算高效的方式集成指数量级数量的$Q$函数估计。与Ensemble DQN相似，该算法也利用$K$个$Q$函数估计$Q$值。利用该$K$个$Q$函数的凸组合作为$Q$值的估计值，即$K-1$单纯形，网络架构可见图1所示，其损失函数为
$$
\begin{aligned}
\mathcal{L}(\theta)=\mathbb{E}_{s,a,r,{s}'\sim\mathcal{D}}[\mathbb{E}_{\alpha\sim P_{\Delta}}[\mathcal{l}_{\lambda}(\Delta_{\theta}^\alpha(s,a,r,{s}'))]] \\
\Delta_{\theta}^{\alpha}(s,a,r,{s}')=\sum_{k}\alpha_k Q_{\theta}^k(s,a)-r-\gamma\underset{{a}'}{max}\sum_k\alpha_k Q^k_{{\theta}'}({s}',{a}')
\end{aligned}\tag{4}
$$
式(4)中$P_{\Delta}$表示$Q$函数$K-1$单纯形$\Delta^{k-1}=\{\alpha\in\mathbb{R}^K:\alpha_1+\alpha_2+\cdots+\alpha_K=1,\alpha_k\ge0,k=1,\ldots,K\}$的概率分布。

在文献[3]中，直接利用均匀分布表示$P_{\Delta}\sim U(0,1)$ ，也即从均匀分布$U(0,1)$采样${\alpha}'_k$，然后再归一化$\alpha_k=\frac{{\alpha}'_k}{\sum{\alpha}'_i}$。

相关思考

$$
\begin{aligned}
Q^{*}(s,a)=\mathbb{E}R(s,a)+\gamma\mathbb{E}_{{s}'\sim P}\underset{{a'\in\mathcal{A}}}{max}Q^{*}({s}',{a}')
\end{aligned}\tag{5}
$$

REM算法把Q-learning视作基于Bellman最优约束(5)的约束满足问题。那么，损失函数(4)可视为不同混合概率分布的无穷数量约束。这种基于集成的方式隐式的考虑了Q函数估计的方差或回报的密度分布[4]，从而把估计不确定性考虑进去，以提高离线强化学习算法的泛化性能。

参考文献

[1] Levine S, Kumar A, Tucker G, et al. Offline reinforcement learning: Tutorial, review, and perspectives on open problems[J]. arXiv preprint arXiv:2005.01643, 2020.

[2] Prudencio R F, Maximo M R O A, Colombini E L. A survey on offline reinforcement learning: Taxonomy, review, and open problems[J]. IEEE Transactions on Neural Networks and Learning Systems, 2023.

[3] Agarwal R, Schuurmans D, Norouzi M. An optimistic perspective on offline reinforcement learning[C]//International Conference on Machine Learning. PMLR, 2020: 104-114.