EfficientNet：重新思考CNN网络的扩展

在视觉领域，网络越深模型的精度越高，但是越深也意味着参数越多，从而需要越多的内存。因此，EfficientNet作者们围绕是否存在一个准则可以扩展卷积网络从而实现更高的精度和效率这一问题，研究了卷积网络的扩展。实验研究发现，平衡网络的宽度、深度、以及分辨率对性能很重要，而且这种平衡可通过一个常量系数扩展网络所实现。由此，作者们提出了复合扩展，如图1所示。

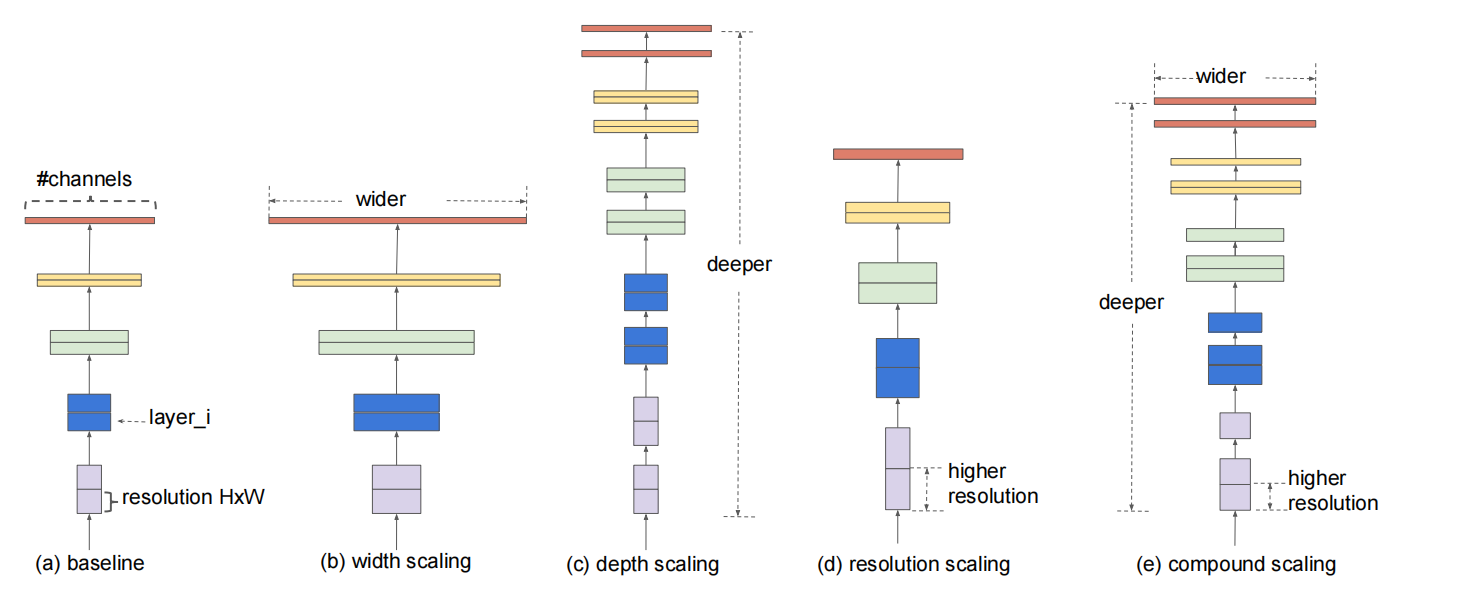
图1 模型扩展

在复合扩展背后有一个直觉：若输入图片越大，那么网络需要更多的层增加感受野和更多的通道捕获图片上更精细模式。确切来说，与经典的任意扩展不同，复合扩展是一种以固定扩展系数均匀扩展网络宽度、深度、以及分辨率的方法。例如：若有$2^{N}$倍的计算资源，那么可简单的增加网络深度$\alpha^{N}$、宽度$\beta^{N}$倍、以及图片大小$\gamma^{N}$倍。其中，$\alpha,\beta,\gamma$为原始模型上进行小的网络搜索确定的。

复合模型扩展

问题定义

若卷积网络层$i$被定义为函数$Y_i=\mathcal{F}(X_i)$，那么卷积网络$\mathcal{N}$可被表示为$\mathcal{N}=\mathcal{F}_k\bigodot\ldots\bigodot\mathcal{F}_2\bigodot\mathcal{F}_1(X_1)=\bigodot_{j=1\ldots k}\mathcal{F}_j(X_1)$。在具体实践中，卷积网络被分为多个阶段，每个阶段的所有层共享相同的架构，那么卷积网络被定义为
$$
\begin{aligned}
\mathcal{N}=\underset{i=1\ldots s}{\bigodot}\mathcal{F}_{i}^{L_i}(X_{<H_i,W_i,C_i>})
\end{aligned}\tag{1}
$$
式(1)中$\mathcal{F}_i^{L_i}$表示在阶段$i$中层$F_i$被重复$L_i$次，$<H_i,W_i,C_i>$表示层$i$输入$X$的维度。

常规的卷积网络设计关注的是最好的网络架构$\mathcal{F}_i$，模型扩展关注的是扩展网络的长度$L_i$、宽度$C_i$、以及分辨率$(H_i,W_i)$。虽然模型扩展不考虑网络架构$\mathcal{F}_i$的设计，但是其它参数仍存在很大的设计空间。为了进一步减少设计空间，作者们限制网络层必须以一个常量系数均匀的扩展。因此，该问题被定义为
$$
\begin{aligned}
\underset{d,w,r}{max}\quad Accuracy(\mathcal{N}(d,w,r)) \\
s.t.\quad\mathcal{N}(d,w,r)=\underset{i=1\ldots s}{\bigodot}\hat{\mathcal{F}}_i^{d\cdot\hat{L}_i}(X_{<r\cdot\hat{H}_i,r\cdot\hat{W}_i,w\cdot\hat{C}_i>})\\
Memory(\mathcal{N})\le target_memory \\
FLOPS(\mathcal{N})\le target_flops
\end{aligned}\tag{2}
$$

经典扩展方法

网络扩展问题主要困难点是深度、宽度、分辨率三个参数彼此影响，且在不同资源限制下最优值会发生改变。因此，经典的网络扩展方法是只对单一方面进行扩展。然而，随着深度、宽度或分辨率的增加，模型不仅更加难以训练，且准确率的收益效果开始消失，可见图2所示。

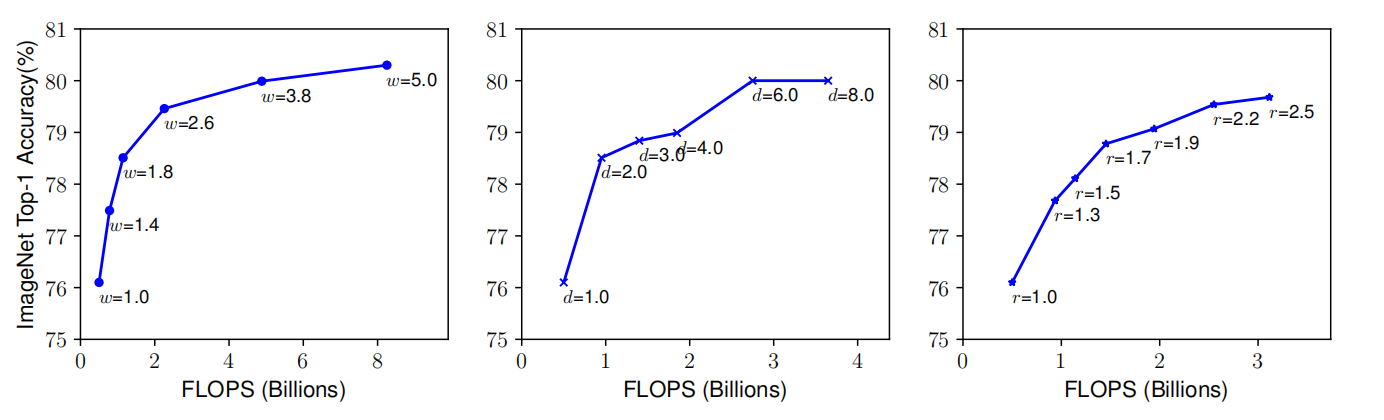
图2 模型经典扩展方法的效果

复合扩展方法

首先，作者们研究了只扩展宽度与三者或两者均扩展在准确率上的不同，如图3所示。

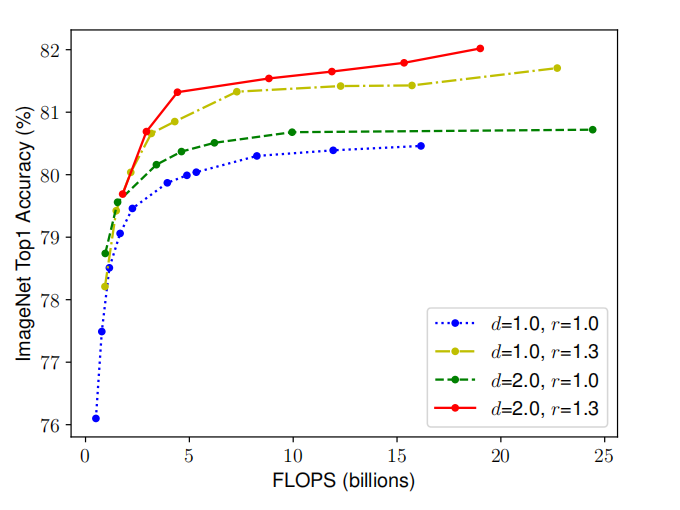
图3 模型经典扩展方法的效果

根据图3，可知，在同样算力下，$d=1.0,r=1.3$、$d=2.0,r=1.0$、以及$d=2.0,r=1.3$的准确率均优于$d=1.0,r=1.0$。由此可见，网络宽度、深度、以及分辨率的平衡的扩展，对模型性能很重要。

在这观察基础之上，作者们提出了复合扩展：
$$
\begin{aligned}
depth:d=\alpha^{\phi} \\
width:w=\beta^{\phi} \\
resolution: r=\gamma^{\phi}\\
s.t.\quad\alpha\cdot\beta^2\cdot\gamma^2\approx2\\
\alpha\ge1,\beta\ge1,\gamma\ge1
\end{aligned}\tag{3}
$$
式(3)中$\alpha,\beta,\gamma$的次方不同是因为深度的增加与算力的增加成正比，而宽度和分辨率增加的平方与算力的增加成正比。$\alpha,\beta,\gamma$参数的确定是通过网格搜索的方式确定。

EfficientNet架构

在已存在较优的网络架构基础上，利用式(3)寻找扩展参数是一种很好的方式。然而，作者们首先基于神经架构搜索较好的网络架构Efficient-B0，然后再寻找扩展参数。如表1所示，Efficient-B0网络架构。

表1 EfficientNet-B0网络架构

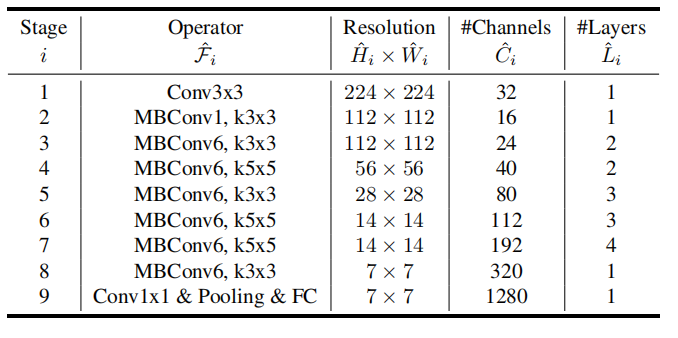
对网络架构，作者们以多目标神经架构搜索的方式寻找架构，其目标函数为$ACC(m)\times[FLOPS(m)/T]^{(w=-0.07)}$，$T$为目标算力，超参数$w$控制精度与算力之间的平衡。EfficientNet中包含的主要模块为移动倒置瓶颈MBConv，其架构搜索空间与MnasNet一致。在网络架构基础之上，执行复合扩展的步骤为：

• STEP 1：固定系数$\phi=1$，即假设存在两倍的资源。基于式(2)和(3)进行网络搜索$\alpha,\beta,\gamma$，得$\alpha=1.2,\beta=1.1,\gamma=1.15$。
• STEP 2：固定$\alpha,\beta,\gamma$，在不同的$\phi$下扩展网络。

虽然直接搜索$\alpha,\beta,\gamma$会产生更好的性能，但是计算量非常大的。因此，分两步搜索扩展系数可以缓和该问题。

相关思考

总的来说，作者们基于直觉：对于更高的分辨率图片，应该增加网络深度，从而获得更大的感受野以获得相似特征。相应的，也应该增加网络深度，从而在高分辨率图片中获得更精细的模式。然后，作者们通过实验验证该直觉。最终，提出了复合扩展。