RoboFlamingo是一款新颖的视觉-语言操纵框架，建立在开源的视觉-语言模型OpenFlamingo基础之上。与之前的框架不同，它利用预训练的VLMs作为视觉-语言理解，基于明确的策略head建模序列历史信息，且只是在语言为条件的模仿学习操纵数据集上微调。最终，RoboFlamingo能够灵活的使用开环控制，且能够部署在低成本的设备上，模型的训练与评估也只是基于单个GPU的服务器实现。如图1所示，RoboFlamingo框架。

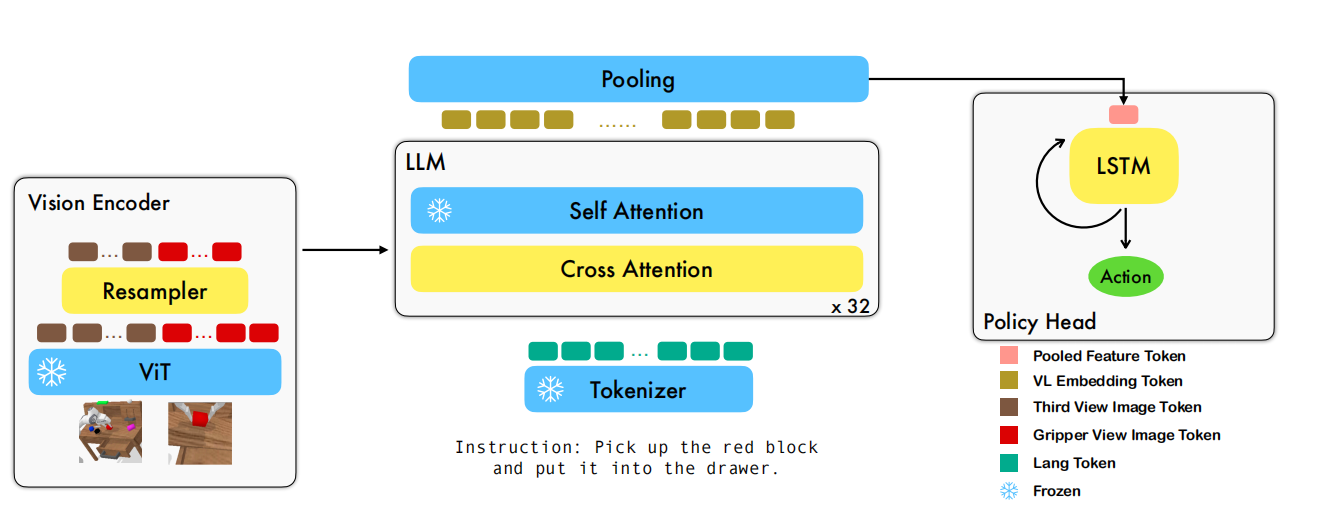
图1 RoboFlamingo框架

RoboFlamingo

RoboFlamingo是一个通用机器人智能体，擅长解决以语言指令为条件的操纵任务。它背后主要的思想是：从视觉-语言模型汲取帮助，从而获得对象识别、语言理解、视觉-语言对齐、以及长期规划的能力。为了实现该目标，需要解决三大挑战：

  • 静态图片输入的视觉-语言模型能够处理视频观测数据。
  • VLM输出机器人控制信号，而不是语言文本。
  • 只利用有限的机器人操纵数据从而实现高性能和较强的泛化性。

基于语言指令的控制

语言为条件的控制被建模为目标为条件的部分可观测马尔可夫决策过程(GC-POMDP)：$\mathcal{M}=<\mathcal{S},\mathcal{O},\mathcal{A},\mathcal{T},\rho_0,\mathcal{L},\phi,f>$

  • $\mathcal{S},\mathcal{O}$分别为状态集合和观测集合。
  • $\mathcal{A}$为动作空间。
  • $\mathcal{T}:\mathcal{S}\times\mathcal{A}\to\mathcal{S}$为环境转换函数。
  • $\rho_{0}:\mathcal{S}\to[0,1]$为初始状态分布。
  • $\phi(s)$为任务的执行状态。
  • $f(o\vert s):\mathcal{S}\to\mathcal{O}$为观测函数。
  • $l\in\mathcal{L}$为长度为M的语言指令。

观测$o_t$由第三视角的图片$I_t$和夹抓上摄像头的图片$G_t$构成，控制策略被建模为目标为条件的策略$\pi(a\vert o,l):\mathcal{S}\times\mathcal{L}\to\mathcal{A}$。

在RoboFlamingo中，策略$\pi_{\theta}(a\vert o,l)$被$\theta$参数化，它由Flamingo的骨架$f_{\theta}$和策略head$p_{\theta}$构成。其中，$f_{\theta}$输出视觉和语言隐融合表示$X_{t}=f_{\theta}(o_t,l)$，策略输出完成目标$l$的动作$a_t=p_{\theta}(X_t,h_{t-1})$。$h_{t-1}$为编码历史信息的隐藏层状态。

Flamingo

视觉编码器

视觉编码器由T2T-ViT和感知器重采样器Perceiver-Resampler构成。在每个时间步$t$，ViT以$I_t,G_t$为输入，输出长度为$N$视觉编码$\hat{X}_t$
$$
\begin{aligned}
\hat{X}_t^v=ViT(I_t,G_t)
\end{aligned}\tag{1}
$$
编码之后，感知器重采样器压缩视觉编码$\hat{X}_t^{v}\in\mathbb{R}^{N\times d}$序列长度由$N$到$N_r$。确切的说，重采样器利用注意力机制减少token序列的长度，可见式(2)所示
$$
\begin{aligned}
K_{R}=\hat{X}_t^{v}W_K^{R},V_{R}=\hat{X}_t^vW_{V}^{R},X_t^v=softmax(\frac{Q_{R}K_{R}^T}{\sqrt{d}})V_{R}
\end{aligned}\tag{2}
$$
式(2)中$Q_{R}\in\mathbb{R}^{N_{r}\times d}$为可学习的查询向量，$d$为隐藏层的维度，$W^{R}_{K},W^{R}_{V}\in\mathbb{R}^{d_v\times d}$表示key与value的线性变换矩阵，$d_v$为视觉token的维度。

特征融合解码器

压缩后的视觉编码$X_t^{v}\in\mathbb{R}^{N_r\times d}$输入到特征融合解码器，最终得到视觉-语言联合embedding。其中，特征融合解码器由$L$层构成，每层由transformer的decorder和交叉注意力层构成。transformer层直接从预训练语言模型中copy得到，且在训练阶段被frozen。交叉注意力层以语言token作为query、视觉token作为key和value为输入，在操纵数据集上微调。

若语言指令的第$i$个embedding用$x_i\in\mathbb{R}^{d}$表示，那么指令的矩阵embedding表示为$X\in\mathbb{R}^{M\times d}$。如式(3)所示，若第$l$层解码器以$X_t^l$为输入，$\hat{X}_t^l$为交叉注意力层输出，$X_t^{l+1}$为最终输出。
$$
\begin{aligned}
\hat{X}_t^l=Tanh(\alpha)\cdot MLP(A(X^{l}_tW^{C}_{Q},X^{v}_tW_K^C,X_t^{v}W_{V}^C)) + X_t^{l},\\
X_t^{l+1}=MLP(A(\hat{X}_t^lW^S_{Q},\hat{X}_t^lW^S_{K},\hat{X}_t^lW_{V}^{S}))+\hat{X}_t^l
\end{aligned}\tag{3}
$$
式(3)中，$\alpha$为控制混合权重的可学习参数，$W_Q^{C},W_K^{C},W_{V}^{C}\in\mathbb{R}^{d\times d}$为交叉注意力层的可学习参数，$W_Q^{S},W_K^{S},W_{V}^{S}\in\mathbb{R}^{d\times d}$为自注意力层的参数。

Policy Head

策略输出head有三种方案：

  • MLP+LSTM
  • Decoder of Transformer + MLP
  • MLP

如式(4)所示，以MLP和LSTM为例。
$$
\begin{aligned}
\tilde{X}_t=MaxPooling(X_t);h_t=LSTM(\tilde{X}_t,h_{t-1});a^{pose},a_t^{gripper}=MLP(h_t)
\end{aligned}\tag{4}
$$

训练目标

目标函数分为两部分，一部分式末端执行器位姿的MSE损失，另一部分是夹抓状态的二分类损失。
$$
\begin{aligned}
l=\sum_tMSE(a_t^{pose},\hat{a}_t^{pose})+\lambda_{gripper}BCE(a_t^{gripper},\hat{a}_t^{gripper})
\end{aligned}\tag{5}
$$

标签: none

版权： 本篇博文采用《CC BY-NC-ND 4.0》，转载必须注明作者和本文链接

添加新评论