实时辐射场渲染的3D高斯喷溅
网格与点云是3常见的3D场景表示,这是因为这些方式非常适合基于GPU快速的光栅化。与之相对,NeRF方法基于连续场景表示,利用捕获场景的新视角合成的体积光线行进对MLP优化。其中,最高效的辐射场景解决方案主要通过对在体素、哈希网格或点云之间插值实现渲染。虽然这些方法中的连续性有助于优化,但是随机采样的成本很高且噪音大。3D高斯喷溅是一种新颖的渲染方法,不仅能够实现实时渲染,而且渲染质量高,可见图1所示。
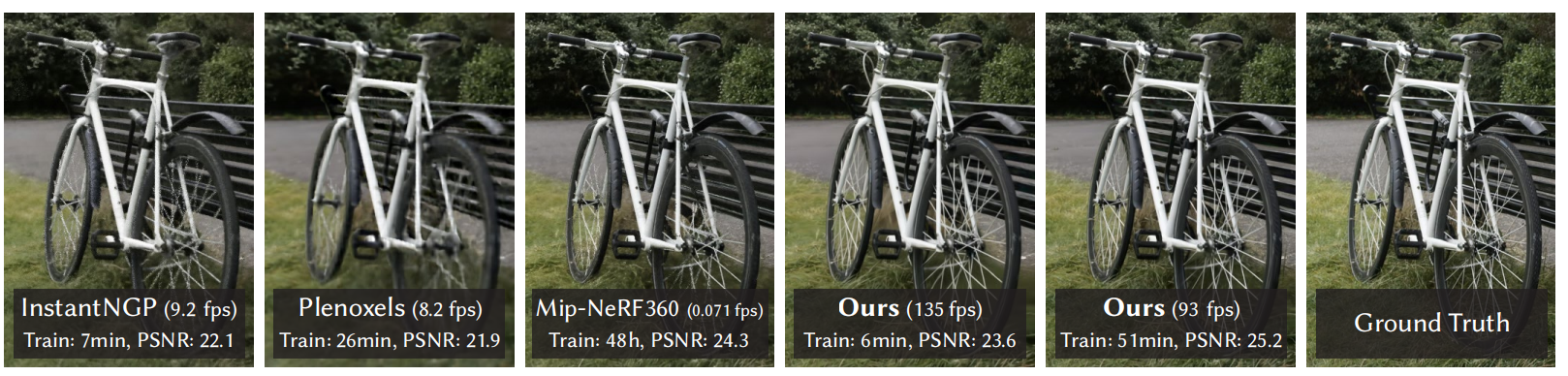
图1 3D高斯喷溅的渲染效果
3D高斯喷溅实现实时渲染主要依赖三个元件,分别是:
- 各项异性3D高斯作为辐射场高质量、无结构的表示。
- 3D高斯特性的优化方法,且与自适应密度控制相互交织,从而创建高质量捕获场景的表示。
- 一个快速、可微分的GPU渲染方法,这种方法允许各向异性喷溅和快速反向传播以实现高质量新视角合成。
算法设计
与NeRF类方法一致,该方法利用SfM校准的相机参数和静态场景图片集合作为输入,且利用SfM过程中产生的稀疏点云初始化3D高斯。同时,与大部分需要Multi-View Stereo(MVS)的基于点云的渲染解决方案不同,该方法只利用SfM点就可以实现高质量结果。3D高斯只所以拥有性能优越的表示方式,这是因为其是一个可微分体积表示,且可高效的投射到2D空间,即光栅化效率高。如图2所示,3D高斯喷溅渲染方法概览。
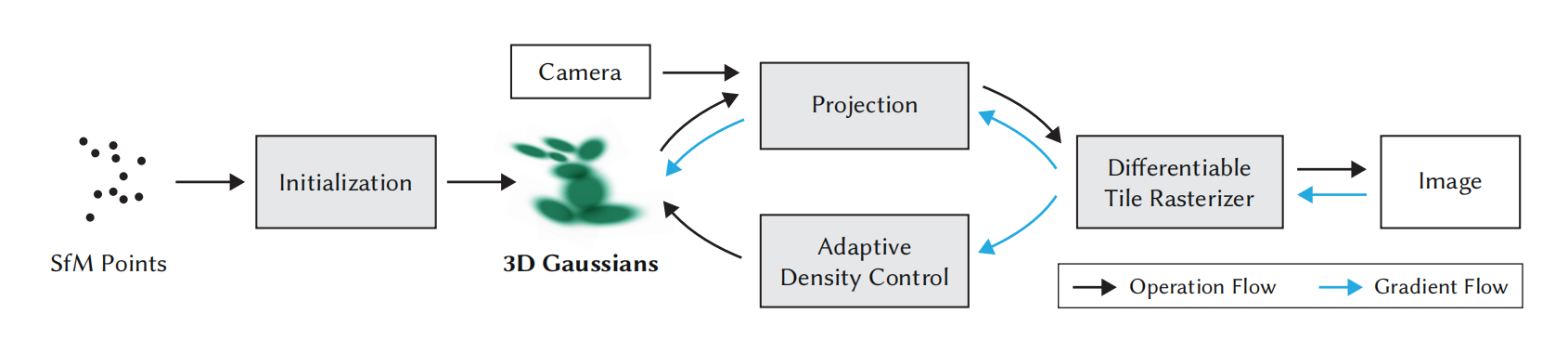
图2 从稀疏SFM点开始的优化与3D高斯集合的创建
可微分的3D高斯喷溅
基于3D高斯建模几何不需要法线。其中,3D高斯被以均值$\mu$为中心的世界空间定义的协方差矩阵$\Sigma$所定义:
$$
\begin{aligned}
G(x)=e^{-\frac{1}{2}(x)^T\Sigma^{-1}(x)}
\end{aligned}\tag{1}
$$
在混合过程中,式(1)中高斯需要与$\alpha$相乘。
然而,对于渲染需要把3D高斯投射到2D空间。给定视角变换$W$,相机坐标下的协方差矩阵${\Sigma}'$为
$$
\begin{aligned}
{\Sigma}'=JW\Sigma W^TJ^T
\end{aligned}\tag{2}
$$
式(2)中$J$为投射变换的雅可比放射近似。
Zwicker等人表明,若移除掉矩阵${\Sigma}'$的第三行与第三列,那么得到一个$2\times2$的方差矩阵。该方差矩阵与Kopanas等人工作中带有法线的平面点拥有相同的结构与性质。然而,协方差矩阵只有为半正定情况下才有物理意义。同时,对于所有参数的优化,梯度下降无法很容易产生有效的矩阵。
因此,作者们选择一个更直观、更具有表达性的表示进行优化。3D高斯的协方差矩阵$\Sigma$可类别于描述椭圆体的配置参数。给定缩放矩阵$S$和旋转矩阵$R$,那么协方差矩阵为
$$
\begin{aligned}
\Sigma=RSS^TR^T
\end{aligned}\tag{3}
$$
为了避免自动微分需要大量的计算,作者们推导了所有参数的梯度,详情可见论文appendix A。协方差各向异性的表示使3D高斯能够表示不同形状的几何。
3D高斯雪球自适应密度控制的优化
优化步骤创建了一个3D高斯雪球稠密集合,用于精确表示自由合成的场景。除了位置$p,\alpha,$以及协方差矩阵$\Sigma$,作者们也优化了表示每个高斯雪球颜色$c$的SH系数。这些参数交错优化的步骤,控制着更好表示场景的高斯密度。
优化
优化是基于渲染与数据集不同训练视角产生图像之间比较的连续迭代。因此,优化需要创建几何,也能够毁坏或移动没有被正确放置的几何。3D高斯协方差矩阵的参数质量对于表示的紧凑性很重要,这是因为大的同质区域可被少量大的各向异性高斯表示。
作者们利用随机梯度下降技术进行优化,充分利用标准GPU加速框架的优势。为了限制透明度$\alpha$的范围为$[0,1)$,使用了Sigmoid激活函数;为了限制协方差的范围,使用了指数激活函数。
初始协方差矩阵的估计是同质高斯,其协方差矩阵中的值为最近三点距离的均值。与Plenoxels相似,利用指数衰减调度技术,但是只对位置参数。损失函数为$\mathcal{L}_1$与D-SSIM项相结合:
$$
\begin{aligned}
\mathcal{L}=(1-\lambda)\mathcal{L}_1+\lambda\mathcal{L}_{D-SSIM}
\end{aligned}\tag{4}
$$
式(4)中$\lambda=0.2$。损失函数论文中没有给出详细介绍,需要进一步阅读Neural Point Catacaustics。
高斯雪球的自适应控制
自适应的控制高斯雪球的数量和对应单位体积的密度,使高斯雪球集合的数量由初始的稀疏集合变为稠密集合,从而更好的表示场景。在优化预热之后,每100个迭代增加高斯雪球的密度,且移除任何透明的高斯雪球,也就是:移除透明度系数$\alpha$小于阈值$\epsilon_{\alpha}$的高斯雪球。
高斯雪球的自适应控制主要关注丢失几何特征的区域和高斯覆盖场景较大的区域。同时,这两个区域拥有较大的视图空间位置梯度。直觉上,这可能是因为这两个区域还没有被很好的重建,即这两个区域是稠密化很好的候选区域。
如图3所示,两种区域自适应稠密化过程。
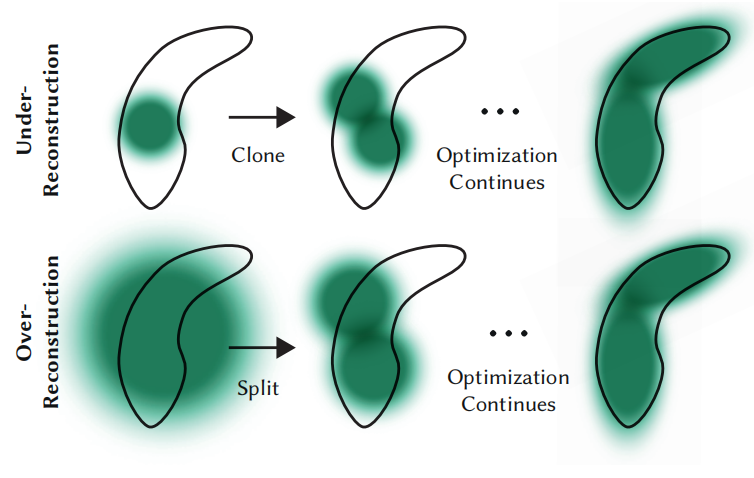
图3 自适应稠密化原理图
对于小高斯,其属于under-reconstructed区域,则需要覆盖新的几何。最常用的方式是复制高斯雪球,即创建同样尺寸的高斯且沿着位置梯度方向移动。
对于大高斯,其拥有较大的方差,则需要把大高斯分裂为相对小的高斯。通常利用两个新高斯替换一个大高斯,即方差被缩放为1.6倍。高斯雪球的位置利用原始的3D高斯分布作为概率密度函数进行采样得到。
对于第一种情况,作者们同时增加系统体积和高斯雪球的数量;对于第二种情况,作者们保存体积而不增加高斯雪球的数量。与其它体素表示相似,这种优化也容易受困于相机附近的漂浮物,从而不合理的增加高斯雪球密度。缓和这种高斯雪球增加的方法是:每3000次迭代,设置$\alpha$值接近于0;接下来,增加需要高斯雪球位置的$\alpha$值且移除$\alpha$小于$\epsilon_{\alpha}$的高斯雪球。高斯雪球可能会缩小或变大,且彼此相互重叠。因此,作者们周期性移除在世界空间中很大与视图空间很大的高斯雪球。优化与稠密化的伪代码,可见算法1。

高斯雪球的快速可微分光栅化器
场景表示的视角渲染是通过point splatting的方式实现,所有的高斯雪球被投射到2D图像屏幕,其颜色的计算来自于球形谐波参数。首先,screen被分为$16\times16$个片。接下来,精选与视图交叉置信度为99%的3D高斯雪球。同时,利用一个守护带拒绝极端位置的高斯雪球,从而避免了2D投射的不稳定问题。然后,根据重叠片的数量初始化每个高斯,且分配一个组合视角空间深度和片ID为64位的键,低32位编码深度,高32位编码索引。接下来,基于这些键利用GPU基数排序对高斯雪球排序。与其它方法相比,$\alpha$混合中每个像素不需要再排序,只需要根据初始排序进行混合,从而提高了训练和渲染效率。
在高斯雪球排序之后,通过识别每个片的第一个和最后一个深度排序雪球,产生一个列表。为了光栅化,作者们为每个片开启了一个线程。首先,每个线程共同加载高斯雪球包到共享内存;然后,对于给定的像素,按照顺序积累颜色和$\alpha$值,指导$\alpha$值趋近于1停止对应的分片。其中,$\alpha$值的饱和度为唯一的停止标准。光栅化的伪代码,可见算法2所示。

在反向传递过程中,需要恢复前向过程中每个像素所有混合点。为了避免存储每个像素所有混合点的动态内存管理运算,作者们选择再次遍历每个片段,即再次利用前向过程中的片段范围和已排序的高斯雪球数组。为了便于计算梯度,从后往前遍历。
在原始的混合过程中,梯度计算需要累积每步的透明度值。在后向传递过程中,作者们没有遍历一个明确逐渐缩小的透明度,而是在前向过程结束时存储透明度值的总和,用于恢复透明度值,作为梯度计算的系数。
引用方法
请参考:
li,wanye. "实时辐射场渲染的3D高斯喷溅". wyli'Blog (Mar 2024). https://www.robotech.ink/index.php/archives/367.html
或BibTex方式引用:
@online{eaiStar-367,
title={实时辐射场渲染的3D高斯喷溅},
author={li,wanye},
year={2024},
month={Mar},
url="https://www.robotech.ink/index.php/archives/367.html"
}