大语言模型的低秩适应技术LoRA的原理

自然语言处理领域许多应用需要微调大规模预训练语言模型，使其适应多个下游任务。然而，这种方式需要更新整个预训练模型的参数，造成微调大模型和部署大模型的成本很高。根据Li和Aghajanyan等人的研究，可知，参数量大的模型的性能实际上依赖于低的固有维度。因此，LoRA作者们假设模型在微调时，权重的改变也有一个低的“内在秩”。如图1所示，LoRA的重参数化方法。

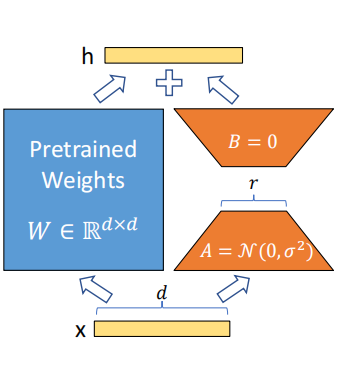
图1 LoRA的重参数化方法

在适应下游任务过程中，LoRA通过优化dense层的秩分解矩阵且保持预训练权重forzen的方式，非直接的优化神经网络。对于Transformer模型，LoRA对预训练权重freeze，在架构的每一层注入可训练秩分解矩阵。

确切的说，对于预训练权重矩阵$W_0\in\mathbb{R}^{d\times k}$，那么LoRA使大模型适应下游任务的方法是$W_0+\Delta W=W_0+BA$，其中$B\in\mathbb{R}^{d\times r},A\in\mathbb{R}^{r\times k}$，且$r\lt min(d,k)$。在模型训练时，$W_0$被frozen，只训练$A$和$B$。利用高斯分布初始化$A$，对$B$进行0初始化，从而使初始时$BA$为0。那么，对于$h=W_0x$，LoRA对模型的修改为
$$
\begin{aligned}
h=W_0x+\Delta Wx=W_0x+BAx
\end{aligned}\tag{1}
$$
然后，作者们通过$\frac{\alpha}{r}$对$\delta Wx$进行缩放。其中，$\frac{\alpha}{r}$为常数。若优化器为Adam，只要合适的缩放初始化，那么调节$\alpha$与调节学习率几乎一致。因此，作者们设置$\alpha$为第一个$r$，不再进行调节。根据TP4，可知，在变化$r$时，这种缩放有助于减少调节超参数的需要。