基于ACT算法与ALOHA实现精细的双臂操作任务

精细的操作任务包含精确的闭环反馈，需要高度的手眼协调从而对环境的变换做出调整和规划。以打开调料杯为例，初始化在桌面上的杯子：先用右手把它拿起，再把它推入到左夹抓。然后，左夹抓慢慢闭上。接下来，右手的手指接近杯子，打开调料杯。这些步骤需要高度的精确性，精细的手眼协调，且丰富的接触。毫米的误差就会导致任务失败。对于这种精细的操作任务，存在的系统需要利用昂贵的机器人和高端传感器用于精确的状态估计。与之相比，ALOHA是一个低成本的灵活远程操作系统，可用于收集数据。然而，低成本硬件不可避免与高端系统相比缺少精确性。为了解决该问题，ALOHA作者们受到Action Chunking的思想设计了模仿学习算法ACT。同时，为了进一步提升模仿学习算法的平滑性和缓和符合误差，提出了Temporal Ensembling。

ALOHA

ALOHA设计遵循的原则：

• 低成本
• 多功能
• 用户友好
• 可修复性
• 容易构建

图1 ALOHA

ALOHA可执行的任务类型：

• 精确任务，例如：连接电缆线
• 丰富接触任务，例如：组装链条
• 动态任务，例如：接乒乓球

ACT

对于ACT算法来说，观测由follower机械臂的目前关节位置与4个相机的图片构成。模仿学习数据的收集由操作ALOHA的leader机械臂收集得到。ACT算法的预测结果由一序列未来动作构成。其中，follower机械臂的关节位置由高频的PID控制器追踪目标位置。

动作分块与时序集成

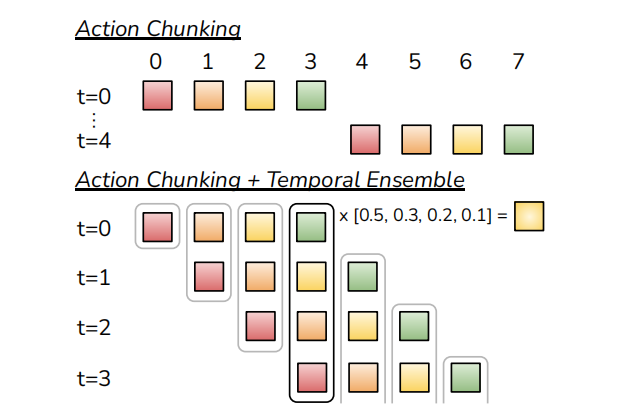
图2 在执行动作时，同时采用ACT与时序集成，而不是动作与观测之间的交替

为了应对模仿学习中的复合误差，作者们减少了收集到长轨迹的有效窗口，就是把完成任务的整个动作进行了分块。该方法是受到神经科学中action chuncking的启发，把动作分组并作为一个单元执行，从而更高效的存储与执行。在具体实现中，作者们设置块的大小为$k$，每$k$步，智能体收到一个观测，生成未来$k$步的动作，执行序列中的动作，可见图2所示。确切的说，策略模型为$\pi_{\theta}(a_{t:t+k}\vert s_t)$，而不是$\pi_{\theta}(a_t\vert s_t)$。这种分块的方式也有助于建模非马尔可夫性，因为行为不仅取决于状态，也取决于时间步。

然而，若每$k$步包含一个环境观测，那么可能导致机器人跳跃式运动。为了提升平滑性与避免执行和观测之间切换的离散性，作者们每个时间步都查询动作。如图2所示，作者们提出了时序集成，用于结合这些预测。确切的说，时序集成通过对这些预测求加权平均，其权重为$w_i=exp(-m*i)$，$m$用于控制包含新观测的速度。确切的说，这里的时序集成是对同一时间不同观测下的预测进行加权集成。

对演示数据进行建模

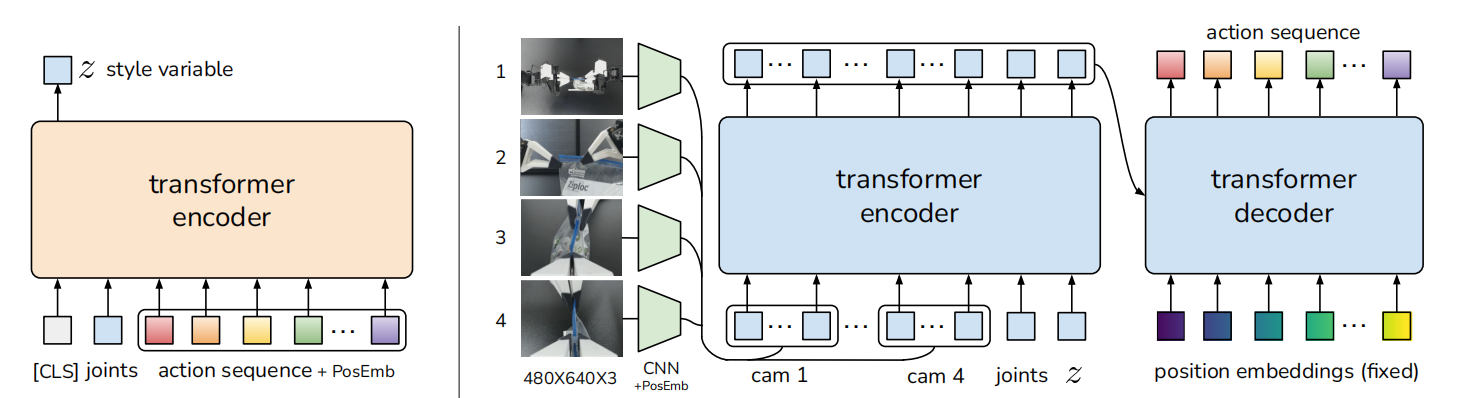
图3 ACT架构

对于相同的观测，人类可利用不同的轨迹解决任务。同时，对于精度不重要的区域，人类的行为更随机。因此，对机器人在高精度很重要区域操作的研究是很重要的。为了解决该问题，作者们基于条件变分自编码器设计了CVAE，以当前观测为条件生成动作序列。如图3所示，CVAE有两个元件，分别是编码器和解码器。其中，编码器在模型推理阶段被抛弃掉了，解码器的输入$z$被设置为0。确切的说，编码器被参数化为对角高斯分布，以当前本体观测与动作序列为输入，用于预测风格变量$z$的均值与方差。为了加快训练，编码器的输入不包含图片数据。对于解码器，其输入为$z$与当前观测。整个模型的目标函数为演示动作分块的log似然$\underset{\theta}{min}-\sum_{s_t,a_{t:t+k\in\mathcal{D}}}log{\pi_{\theta}}(a_{t:t+k}\vert s_t)$作为重构损失与正则化编码器为高斯先验项构成。与$\beta$-VAE一致，正则化项的系数为$\beta$，从而控制隐式信息通道容量与学习统计上独立的隐式因子的程度。根据深度学习与信息瓶颈原则，可知，$\beta$值越高，其变量$z$信息传输的越少。

ACT的实现

对于CVAE编码器，作者们利用BERT作为网络架构，其输入为当前关节位置与演示数据集中长度为$k$的目标关节序列，且输入序列前置一个可学习token"[CLS]"。从而，形成了$k+2$长度的输入。

对于CVAE解码器，网络架构为Transformer，其输入为当前观测与$z$。对于图片数据，作者们利用ResNet18进行编码。确切的说，观测包括分辨率为$480\times640$的4个RGB图片，与两个机械臂的关节位置构成；动作空间为两个机械臂的关节位置，共14维。因此，策略的输出维度为$k\times14$。对于图形数据，ResNet18把其由$480\times640\times3$转换为$15\times20\times512$特征地图，然后沿着空间维度被打平为$300\times512$。同时，为了保存空间信息，增加2D正弦位置编码。对于4张图片，特征序列为$1200\times512$。从而，整个输入的大小为$1202\times512$。对于Transformer解码器的输出，其大小为$k\times512$，再利用MLP下采样为$k\times14$。对于重构损失函数，利用$L_1$而不是$L_2$，这是因为$L_1$会导致动作序列更精确的建模。

ACT算法的训练与推理，可见算法1与算法2所示。

ACT算法的实践经验

在实践中，发现， ACT的动作分块与时序集成虽然提高了模型执行静态任务时的时序依赖能力，但是限制了模型适应操作物品动态变化的能力。同时，若对一个块的动作有较大的扰动，会导致机械臂无法完成任务。