FLD：结构化运动表示与学习的傅利叶隐式动力学

参考轨迹的可用性极大地推动了运动学习技术的进步。然而，这些技术的泛化性很差。这是因为基于轨迹数据学习得到的策略往往只是记住轨迹实例，而不是理解潜在的动力学结构。同时，高度的非线性与嵌入的高级别相似性阻碍了有效识别与建模运动模式的动力学。与直接从高维状态空间处理原始轨迹数据不同，结构化表示方法在训练期间引入了特定的推断偏差且提供了管理复杂运动的高效方法。FLD是PAE的生成式扩展，利用一个新的预测结构在周期或拟周期运动中抽取时空关系。它通过在一个包含重要特征与自然运动时序依赖的连续型参数化隐空间中抽取运动动力学的方式表示高维轨迹，从而提升运动学习算法的专业性与泛化能力。

PAE

尽管自监督学习在复杂任务上取得利成功，但是已有的自监督学习往往忽视了数据中周期性。受到PAE启发，作者们探索了带有明确周期性考虑的表示方法。PAE通过在频率域关注运动的周期性从而应对运动空间的挑战，例如：数据稀缺性与运动空间的高度非线性。如图1a所示，PAE结构。

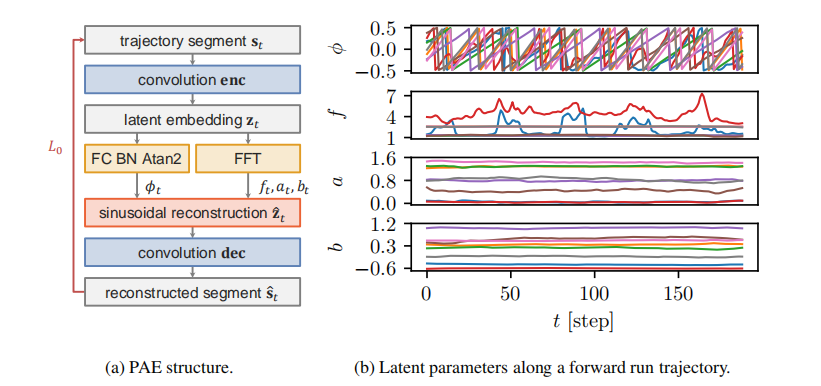
图1 PAE结构与前向运动时隐式参数变化情况

在$d$维状态空间中长度为$H$的轨迹片段被表示为$s_t=(s_{t-H+1},\ldots,s_t)\in\mathbb{R}^{d\times H}$，作为输入。自编器把输入运动分解为$c$个隐式通道的embedding $\mathbf{z}_t\in\mathbb{R}^{c\times H}$。然后，利用快速傅利叶参数化过程$p$获得隐轨迹的频率向量$f_t$、幅度向量$a_t$、与偏置向量$b_t$，还有相向量$\phi_t$。其中，$\phi_t$式利用独立的全连接网络得到。
$$
\begin{aligned}
\mathbf{z}_t=\mathbf{enc}(s_t),\quad \phi_{t},f_t,a_t,b_t=p(\mathbf{z}_t)
\end{aligned}\tag{1}
$$
接下来，利用正弦函数参数化隐向量，用于重构隐式轨迹片段$\hat{\mathbf{z}}_t\in\mathbb{R}^{c\times H}$
$$
\begin{aligned}
\hat{\mathbf{z}}_t=\hat{p}(\phi_t,f_t,a_t,b_t)=a_tsin(2\pi(f_t\mathcal{T}+\phi_t))+b_t
\end{aligned}\tag{2}
$$
式(2)中$\mathcal{T}$为时间窗口与状态转换窗口$H$对应。最后，神经网络把重构隐式轨迹解码到原始运动空间，且利用原始输入计算重构误差
$$
\begin{aligned}
\hat{\mathbf{s}}_t=\mathbf{dec}(\hat{\mathbf{z}}_t),\quad L_0=MSE(\hat{\mathbf{s}}_t,\mathbf{s}_t)
\end{aligned}\tag{3}
$$
式(3)中$\hat{\mathbf{s}}_t\in\mathbb{R}^{d\times H}$

FLD

考虑状态空间$\mathcal{S}$与来自数据集$\mathcal{M}$的运动序列$\tau=(s_0,s_1,\ldots)$，研究目标为创建一个基于物理的学习器，不仅仅能够复制参考数据集中描述的运动，且能够根据新的目标输入相应的生成运动，从而提高模型的泛化性。

傅利叶隐式动力学

通过观察PAE编码的周期或拟周期隐式轨迹参数，作者们发现频率、幅度、以及偏置向量均呈现时间不变性。因此，引入利拟常量参数化假设

假设1：一个隐式轨迹$\mathbf{z}=(\mathbf{z}_t,\mathbf{z}_{t+1},\ldots,)$可被$\hat{\mathbf{z}}=(\hat{\mathbf{z}}_t,\hat{\mathbf{z}}_{t+1},\ldots)$所近似，其有界误差$\delta=\Vert\mathbf{z}-\hat{\mathbf{z}}\Vert$。其中，对于$\forall {t}'\in\{t,t+1,\ldots\}$，$\hat{\mathbf{z}}_{{t}'}=\hat{p}(\phi_{{t}'},f,a,b)$

由于隐特征被学习得到，因此假设1可被确切的实现。在接下来的部分，作者们利用$\phi_t$表示隐状态，$f,a,b$表示隐参数。因此，傅利叶隐动力学可通过局部状态$\phi_t$与全局参数化常量集$f,a,b$传递隐式动力学参数化的方式实现$\mathbf{z}$的重建。

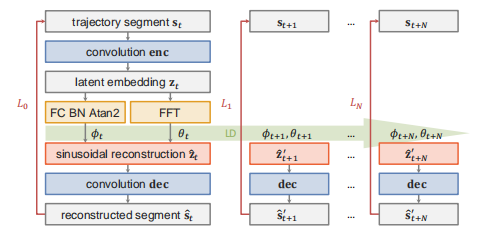
图2 FLD训练流程

如图1所示，FLD与其训练过程。对于运动片段$\mathbf{s}_t=(s_{t-H+1},\ldots,s_t)$，利用第$i$步前向传递${\hat{\mathbf{z}}}'_{t+i}$的解码预测${\hat{\mathbf{s}}}'_{t+i}$近似运动片段
$$
\begin{aligned}
{\hat{\mathbf{z}}}'_{t+i}=\hat{p}(\phi_t+if_t\Delta t,f_t,a_t,b_t),\quad {\hat{\mathbf{s}}}'_{t+i}=\mathbf{dec}({\hat{\mathbf{z}}}'_{t+i})
\end{aligned}\tag{4}
$$
式(4)中$\Delta t$为时间步的时间

那么，损失函数为
$$
\begin{aligned}
L^{N}_{FLD}=\sum_{i=0}^N{\alpha}^iL_i,\quad L_i=MSE({\hat{\mathbf{s}}}'_{t+i},\mathbf{s}_{t+i})
\end{aligned}\tag{5}
$$
通过选择合适的最大化传递窗口与衰减因子，从而在局部重建的准确性与隐式参数化的全局性之间权衡。根据式(5)，可知PAE缺乏时序传递结构且只是利用局部参数化执行局部重建，而FLD可动态调整维度以表达整条轨迹。

运动学习

给定参考轨迹，基于物理的运动学习算法训练一个控制策略，从而模仿仿真人物或机器人的关节，且复制运动指令的轨迹。FLD能够高效的表示丰富的运动集合。与离散或手工运动指示器相比，FLD参数化的隐式空间内的特征距离为学习算法提供了一个运动之间相似性合理的度量。

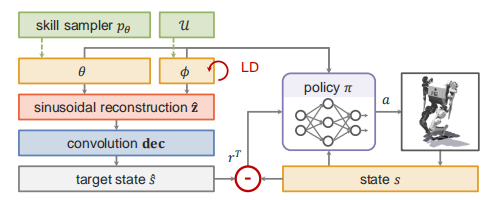
图3 FLD系统概览

策略训练

在每个episode开始，隐式参数空间$\Theta\subseteq\mathbb{R}^{3c}$内的隐式参数$\theta_{0}\in\mathbb{R}^{3c}$是由基于技能采样器$p_{\theta}$采样得到。隐式状态$\phi_{0}\in\mathbb{R}^c$均匀的从固定范围$\mathcal{U}$中采样得到。隐式向量根据式(4)中隐式动力学更新
$$
\begin{aligned}
\theta_t=\theta_{t+1},\quad\phi_t=\phi_{t-1}+f_{t-1}\Delta t
\end{aligned}\tag{6}
$$
每一步，隐式状态与隐式参数化被用于重构运动片段
$$
\begin{aligned}
\hat{\mathbf{s}}_t=(\hat{s}_{t-H+1},\ldots,\hat{s}_t)=\mathbf{dec}(\hat{\mathbf{z}}_t)=\mathbf{dec}(\hat{p}(\phi_t,\theta_t))
\end{aligned}\tag{7}
$$
式(7)最近状态$\hat{s}_t$作为学习环境的追踪目标。

如图3所示，训练流程的原理图。其中，隐状态与参数化被用于构成观测空间，从而使策略知道需要追踪目标。算法伪代码可见算法1所示。

线上追踪与Fallback机制

在推理阶段，策略结构包含一个实时运动输入作为追踪目标。为了确保参考输入与训练数据分布相接近，基于式(5)的重构误差度量参考轨迹与训练数据中轨迹的不一致性。通过设定阈值$\epsilon_{FLD}$的方式，作为Fallback机制。如图4所示，线上追踪与fallback机制原理图。

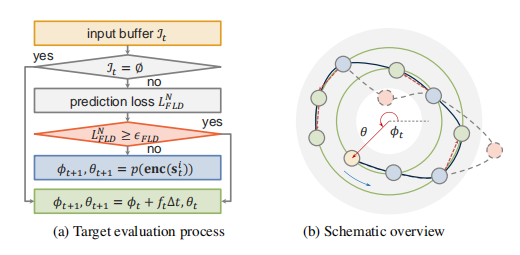
图4 线上追踪与fallback机制

相关思考

总的来说，FLD通过自监督学习得到运动目标的隐式状态与隐参数，再利用强化学习追踪该目标。根据自己的理解，FLD只在熟悉的领域进行泛化，对于不熟悉的领域直接抛弃掉。