Consistency Policy：通过一致性蒸馏加速视觉运动策略

由于空间、重量、以及电量的约束，大部分机器人系统无法配备高端GPUs。扩散策略在机器人控制的模仿学习领域实现了惊人的性能。然而，扩散策略的推理速度较慢，需要多步迭代才能生成动作。这种推理速度慢的约束限制了扩散策略的应用范围。为了保留扩散策略的性能且减少推理时间，Consistency Policy作者们通过对扩散策略的蒸馏，得到了一致性策略。

这种方式把训练一个扩散模型视作求解一个ODE，利用ODE解的唯一性和相同ODE轨迹不同位置开始去噪之间的一致性，从而对扩散模型进行蒸馏，实现模型的快速推理。首先，作者们利用EDM框架训练扩散模型，再利用一致性轨迹模型(CTM)目标的改进版进行模型蒸馏。其中，关键的设计决策包含一致性目标、降低初始样本方差、以及预先设定步数的选择。同时，作者们也对CTM目标特定区域的dropout角色提出了洞见，以及一致性策略对teacher质量的鲁棒性进行了分析。

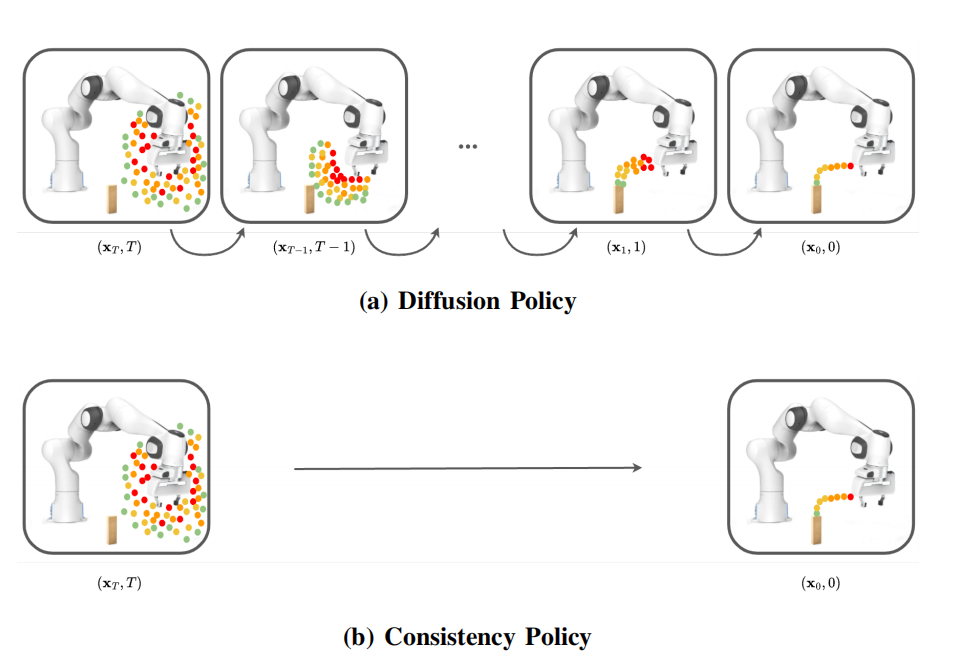
图1 扩散策略与一致性策略在不同阶段的预测动作序列分布

基础知识

扩散模型学习从单位高斯分布$\mathcal{N}(0,\mathbf{I})$随机采样动作$\mathbf{x}_T$到以当前观测为条件的专家动作分布采样特定动作$\mathbf{x}_0$的映射。其中，$0\le t\le T$指在时刻$T$从简单高斯分布采样点到在时刻0的复杂数据分布映射轨迹上的时刻点。

该过程常被阐述为概率流常微分方程(PFODE)，随着时间向前演化PFODE对动作增加噪音，随着时间向后演化PFODE对动作去除噪音，其通用形式为
$$
\begin{aligned}
d\mathbf{x}_t=[\mu(\mathbf{x}_t,t)-\frac{1}{2}\sigma(t)^2\nabla p_{t}(\mathbf{x}_t\vert o)]
\end{aligned}\tag{1}
$$
式(1)中$\mu(\cdot,\cdot)$为飘逸系数，$\sigma(\cdot)$为扩散系数，以及$p_t(\mathbf{x}_t\vert o)$为时间$t\in[0,T]$的噪音概率分布。为了使$p_{T}(\mathbf{x}_t\vert o)$接近标准正态分布，$T$应该足够大。EDM中设置$\mu(\mathbf{x}_t,t)=0$和$\sigma(t)=\sqrt{2t}$。

噪音概率分布的梯度$\nabla logp_t(\mathbf{x}_t\vert o)$被称为分数，由于不可计算，所以常用神经网络近似。

训练分数模型近似器需要大量的目标，所以需要在原始训练数据集中先执行前向扩散过程。在时刻$t$，无标准化被扰动的分布$p_t(\mathbf{x}_t\vert o)$等于原始数据分布$p_0(\mathbf{x}\vert0)$与$\mathcal{N}(0,t^2I)$的卷积。采样一个特定$\mathbf{x}_t\sim\mathcal{N}(0,I)$，可先采样$\epsilon\sim\mathcal{N}(0,I)$，再乘以$t$，再与原始数据相加得到$\mathbf{x}_t=\mathbf{x}+t*\epsilon$。在把位置传递到分数函数近似器之前，一般会进行标准化，从而有单位方差。

一致性策略训练

为了训练一个能够进行少量或单步生成的模型，作者们先训练一个teacher模型，然后把它蒸馏到学生模型。

Teacher Model(EDM)

根据EDM框架训练teacher模型$s_{\phi}$。EDM模型以当前位置$\mathbf{x}_t$和时间$t$，以及观测$o$为输入，用于估计PFODE轨迹的导数
$$
\begin{aligned}
\frac{d\mathbf{x}_t}{dt}=-\frac{(\mathbf{x}_t-s_{\phi}(\mathbf{x}_t,t,;o))}{t}
\end{aligned}\tag{2}
$$
EDM模型可被用于沿着PFODE轨迹利用数值积分方法计算$\mathbf{x}$。

EDM模型的损失函数去噪分布匹配损失DSM
$$
\begin{aligned}
\mathcal{L}_{DSM}(\theta)=\mathbf{E}_{t,\mathbf{x}_0,\mathbf{x}_t\vert\mathbf{x}_0}[d(\mathbf{x}_0,s_{\phi}(\mathbf{x}_t,t;o))]
\end{aligned}\tag{3}
$$
DSM目标函数以PFODE轨迹上点$(\mathbf{x}_t,t)$为输入，使EDM预测真实初始位置$\mathbf{x}_0$，度量为$d(\cdot,\cdot)$为pseudo-huber损失
$$
\begin{aligned}
d(x,y)=\sqrt{\vert x-y\Vert_2^2+c^2}-c
\end{aligned}\tag{4}
$$
其中，$c=0.00054\sqrt{D}$，$D$为数据的维度。该损失类似于$l_1$损失与$l_2$损失之间的桥梁，比EDM中$l_2$损失更能应对异常值。对于数值积分求解器，作者们利用Heun's 二阶求解器。

Student Model

CTM作者们提出了一个把teacher模型$s_{\phi}(\mathbf{x}_t,t;o)$蒸馏到student模型$g_{\theta}(\mathbf{x}_t,t,s;o)$的目标函数，使图片生成任务只需要一步或少量推理步数就能实现SOTA结果。student模型以位置$\mathbf{x}_t$，$t$，以及观测$o$为输入，学习估计PFODE起初时刻$s$的位置$\mathbf{x}_s$，其目标函数为DSM损失和CTM损失之和。

直觉上，CTM的目标函数可被理解为沿着PFODE实施自一致性，这是因为相同PFODE轨迹上不同点$(\mathbf{x}_{t},t)$和$(\mathbf{x}_u,u)$应该重构到时刻$0$的相同位置$\mathbf{x}_s$。其中，$0\le s\lt u\le T$。那么，目标函数为
$$
\begin{aligned}
\mathcal{L}_{CTM}=d(g_{\theta}(\mathbf{x}_s^{(t)},s,0;o),g_{\theta}(\mathbf{x}_s^{(u)},s,0;o))
\end{aligned}\tag{5}
$$
其中，
$$
\begin{aligned}
\mathbf{x}_{s}^{(t)}=g_{\theta}(\mathbf{x}_t,t,s;o)
\end{aligned}\tag{6}
$$

$$
\begin{aligned}
\mathbf{x}_{s}^{u}=g_{\theta}(\mathbf{x}_{u},u,s;o)
\end{aligned}\tag{7}
$$

以上三个方程中，唯一参与运算的是$t\to s$的生成过程，即式(6)

对于时刻$t$，从离散时间步中均匀采样。在从$\mathcal{N}(0,t^2\mathbf{I})$采样$\mathbf{x}_t$之后，$\mathbf{x}_{u}$从teacher EDM模型和选择的数值积分器中$t-u$步采样得到，按照式(2)的方式。其中，蒸馏信号通过teacher模型对给定$\mathbf{x}_{t}$下$\mathbf{x}_{u}$的预测得到。

由此，一致性策略的损失函数为
$$
\begin{aligned}
\mathcal{L}_{CP}=\alpha\mathcal{L}_{CTM}+\beta\mathcal{L}_{DSM}
\end{aligned}\tag{7}
$$
在实践中， 一致性模型中表示相邻的$t$与$u$效果最好。其中，跳连接和采样器的细节可见CTM。

一致性策略推理

对于单步推理，先采样初始位置$\mathbf{z}\sim\mathcal{N}(0,I)$，计算$\mathbf{x}=g_{\theta}(z,T,0;o)$，在环境部署动作$\mathbf{x}$。其中，$T$为训练时的最大时间步。相较于从$\mathbf{z}\sim\mathcal{N}(0,T^2I)$中采样，从标准正态分布采样可使初始点接近正态分布的均值，从而减少异常值的出现，且实验表明效果较好。这也与Pearce等人的假设一致的，使输出远离高斯然区域是有害的。

对于三步推理，给定chaining时间步$\{t_1,t_2\}$，先从$T\to 0$去噪，然后再加噪音到$t_1$，再去噪到$0$，然后对剩下的时间步骤进行第二次。通过这种方式，精炼初始预测。对于$t_1$和$t_2$的选择，作者们发现最早期时间级别被发现会调整难以察别和不重要特征，而越大的时间级别形成通用属性或插值到目标分布中心。时间步接近区间早中间隔的会贡献大部分重要特征与细节。因此，作者选择时间步$\{t_{\frac{2N}{3}},t_{\frac{N}{3}}\}$

实现细节

与扩散策略一致，一致性策略仍然是预测动作序列。对teacher模型，作者们选择1D卷积UNet架构。该架构利用FiLM块以观测和扩散步骤$t$为条件，利用1D卷机块进行动作域扩散。

对于student模型，作者们利用相同的架构，但是扩散了FiLM块以容纳停止时间$s$为条件。同时，还利用teacher模型进行热启动，对于扩展的FiLM块部分进行0初始化，从而延时热启动参数的有效性。

之所以选择1D卷积UNet作为网络架构，这是因为扩散策略表明transformer需要更多的超参数调节。