扩散策略：通过动作扩散进行的视觉运动策略学习

基于演示的策略学习是学习观测到动作映射的监督学习任务。然而，现实中机器人动作具有多峰分布、序列相关、以及高精度要求的特点，与其它监督学习任务相比具有很大的挑战。扩散策略是一个新形式的机器人视觉运动策略。与直接预测动作不同，它以视觉观测为条件推断动作-分数的梯度。这种方式学习到的策略继承了扩散模型许多关键特性：

表达多峰的动作分布：通过学习动作分数函数的梯度和在梯度域上执行随机朗之万采样，扩散策略可以表达任意标准化的分布。
高维输出空间：正如极具表达性的图片生成结果展示的，扩散模型对高维空间展现出杰出的扩展能力。这种特性使策略可以推断出未来动作的一个序列。这对于鼓励时序动作的连续性与避免短视规划很重要。
稳定训练：训练基于能量的策略常常需要负采样，用于估计很难估计的正则化常数，这会造成训练的不稳定性。扩散策略绕过了学习能量函数梯度的需要，因此实现了稳定训练。

扩散策略

去噪扩散概率模型

DDPMs被称为去噪扩散概率模型，在图像领域作为生成模型，其输出被建模为去噪过程，常称为随机朗之万动力学。去噪过程可表达为
$$
\begin{aligned}
\mathbf{x}^{k-1}=\alpha(\mathbf{x}^k-\gamma\xi_{\theta}(\mathbf{x}^k,k))+\mathcal{N}(0,\sigma^2\mathbf{I})
\end{aligned}\tag{1}
$$
式(1)中$\xi_{\theta}$为参数$\theta$下噪音预测网络。

根据式(1)，可知，去噪过程为：从高斯噪音采样得到$\mathbf{x}^K$开始，执行$K$次去噪迭代，产生一系列中间动作$\mathbf{x}^k,\mathbf{x}^{k-1},\ldots,\mathbf{x}^0$，直到期望的无噪音输出$\mathbf{x}^0$得到。

公式(1)也可以被理解为噪音梯度下降：
$$
\begin{aligned}
\mathbf{x}'=\mathbf{x}-\gamma\nabla E(\mathbf{x})
\end{aligned}\tag{2}
$$
噪音预测网络$\xi_{\theta}(\mathbf{x},k)$有效的预测了梯度$\nabla E(\mathbf{x})$，$\gamma$为学习率。

DDPM训练

去噪扩散概率模型的训练过程为：从数据集中随机采样得到样本$\mathbf{x}^0$；对于每个样本，随机(通常为均匀分布)选择第$k$次迭代，再从第$k$次迭代的高斯分布中采样噪音$\xi^k$，然后基于MSE损失函数训练噪音预测网络。
$$
\begin{aligned}
L=MSE(\xi^k,\xi_{\theta}(\mathbf{x}^0+\xi^k,k))
\end{aligned}\tag{3}
$$
其中，第$k$次迭代的高斯分布的方差需要满足一定的计算关系，具体可见DDPMs相关论文。

视觉运动策略学习的扩散

在把DDPM用于学习机器人视觉运动策略的过程中，需要修改两个方面，分别是：

输出$\mathbf{x}$用于表示机器人动作
以观测$\mathbf{O}_t$为输入条件进行去噪

图1 扩散策略概览

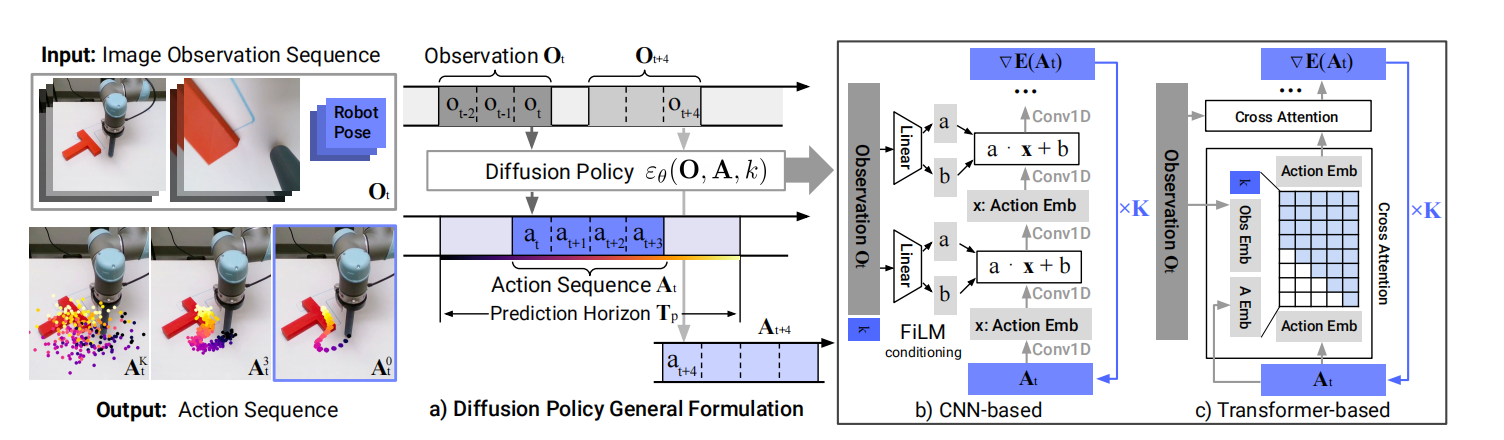
闭环动作序列预测

一个有效的动作函数应该鼓励时序连续性和长期规划平滑性，也能够允许对数据分布之外的观测作出及时响应。为了实现该目标，利用回退窗口控制对扩散模型产生的动作序列进行动作的执行。更确切的说：在时间步$t$，策略基于最近$T_0$个的观测数据$O_t$作为输入，预测出$T_p$个动作。其中，$T_a$个动作用于执行。通过只执行$T_a$个动作，从而使策略实现执行的时序连续性、平滑性，且也能及时响应变化。简单来说，只执行中间的一部分片段。模型的输入与输出可见图1.a所示。

注：这种闭环方式作用是有限的，只是使策略意识到了反馈而已，不是完全的反馈。这种动作序列的预测，有时序连续性和空闲动作鲁棒性的优势。同时，模型预测位置，相较于预测速度，更能应对复合误差，且基于位置控制的模式更能表现动作的多峰分布。在ACT算法实践过程中，发现，动作序列的预测并不会对空闲动作有较强的鲁棒性，可能是该算法表达力不足的原因。

基于回退窗口控制的动作执行效果，可见图2所示。

图2 多峰动作

根据图2可知，在给定状态下，末端执行器可以从左边或右边推动block。扩散策略两种策略都学习到了，且在每个回合只执行一种策略。然而，LSTM-GMM和IBC偏向于一种模式；BeT由于缺乏时序依赖性在一个回合中无法执行任何一个策略。

视觉观测为条件

若以视觉观测为条件预测动作，那么式(1)可变为
$$
\begin{aligned}
\mathbf{A}_t^{k-1}=\alpha(\mathbf{A}_t^k-\gamma\xi_{\theta}(\mathbf{O}_t,\mathbf{A}_t,k)+\mathcal{N}(0,\sigma^2I))
\end{aligned}\tag{4}
$$
式(3)变为
$$
\begin{aligned}
L=MSE(\xi^k,\xi_{\theta}(\mathbf{O}_t,\mathbf{A}_t^0+\xi^k,k))
\end{aligned}\tag{5}
$$
从去噪过程的输出中排出掉观测显著提升了推理速度，且更好地容纳实时控制。

重要的设计决策

网络架构的选择

对于网络架构，作者们给出了两种，分别是基于CNN的扩散策略架构和基于Transformer的扩散策略架构。

对于基于CNN的扩散策略架构，作者们在Diffuser中U-Net网络架构基础上进行了一些改进：

以FiLM编码后的观测Embedding和去噪迭代数$k$为条件，生成动作，可见图3.b所示。
只预测动作轨迹，而不是预测观测和动作的联合轨迹。
由于回退预测窗口的不兼容性，移除基于inpainting的目标状态。

为了减少CNN模型过平滑的效果，引入了BeT中Transformer架构，被称为基于Transformer的DDPM。该模型把共享MLP编码之后的观测$\mathbf{O}_t$Embedding、带有噪音的动作$A_t^k$、以及扩散迭代次序$k$输入到Transformer的解码器中预测“梯度”$\xi_{\theta}(\mathbf{O}_t,\mathbf{A}_t^k,k)$。其中，扩散迭代序列次序$k$为第一个token。

对两个模型的选择，作者们建议先尝试基于CNN的扩散模型。若效果不好，再尝试基于Transformer的模型。根据作者们的实践经验，在任务复杂性或动作变化频率较高的任务上，CNN的效果会差。

确切的说，基于CNN的网络架构本质上是时序卷积，该网络架构有利于每步噪音预测不仅取决于过去时间步，也取决于未来时间步，从而捕获局部时序关系，最终也能保证整体的时序一致性。同时，U-Net网络架构可使输出不仅取决于网络架构，也取决于输入，可使输入与输出一致。与U-Net相比，Transformer网络架构每步的噪音预测只关注过去的信息，主要是为了解决CNN过平滑的问题。

视觉编码

每张图片被ResNet-18编码为embedding，与之前时间步的编码concat到一起，得到最终的观测。同时，也对编码器进行了如下修改：

利用空间softmax池化替换全局平均池化。
利用GroupNorm替换BatchNorm。

噪音调度

$\sigma,\alpha,\gamma$,以及高斯噪音$\xi^k$均为$k$的函数，这种方式被称为噪音调度。它控制着扩散策略捕获动作的高频和低频特性。作者们，发现，iDDPM中平方余弦调度效果最好。

模型推理

在推理阶段，推理速度对实现实时控制非常重要。其中，DDIM中作者们通过解耦合训练与推理时去噪的次数，从而提高模型的推理速度。这种方式在扩散策略中也同样适用。