SNR PUN：为了RL的泛化性而正则化参数不确定性

为了使RL智能体能够部署到真实世界环境，必须要能够泛化到未观察到的环境。然而，RL很困难实现分布外的泛化，这是由于智能体往往过拟合于训练环境的细节。虽然监督学习的正则化技术可以被用于避免过拟合，但是RL与监督学习之间的差别限制了它们的应用。为了处理泛化性问题，SNR PUN作者们提出了信噪比正则化参数不确定性网络。

算法设计

对于RL智能体的正则化，有两种主要的方式，分别是噪音注入和参数正则化。对于噪音注入，主要通过对智能体策略或模型参数引入随机性，从而提升探索行为和阻止过度依赖训练环境的一些特征。然而，这些方法的缺点是在训练过程中引入了扰动，从而干预智能体学习有效策略的能力。对于参数正则化，主要通过直接控制模型的复杂度，从而鼓励网络学习简单的函数，从而实现更好的泛化性。然而，参数正则化往往会导致智能体捕获环境的复杂性，限制智能体学习任务的能力。

与噪音注入和正则化参数相比，参数不确定性为中间地带，它结合了噪音注入的探索能力和参数正则化的结构化能力。

Bayes-By-Backprop

在神经网络中实现参数不确定的常见方式是Bayes-By-Backprop(BBB)，网络参数$\theta=\{\theta_1,\ldots,\theta_N\}$不是确定的值，而是作为一个高斯分布$\theta_i\sim\mathcal{N}(\mu_i,\sigma_i)$。标准差$\sigma_i$通过对辅助参数$\beta_i\in\mathbb{R}$施加softplus函数而确保其为正值。即$\sigma_i=log(exp(\beta_i)+1)$。在前向过程中，参数的值从分布中采样：
$$
\begin{aligned}
\epsilon_i\sim\mathcal{N}(0,1) \\
\theta_i=\mu_i+log(exp(\beta_i)+1)\cdot\epsilon_i,\forall i\in N
\end{aligned}\tag{1}
$$
BBB方法的训练过程主要更新分布的参数，即$\mu_i,\beta_i$，从而在拟合数据的同时确保与预定义的固定先验分布接近。根据定义，损失函数为
$$
\begin{aligned}
\mathcal{L}(\mathcal{D};\theta)=-\mathbb{E}_{q(\theta)}[logp(\mathcal{D}\vert\theta)]+c_{\beta}*KL[q(\theta)\Vert p(\theta)]
\end{aligned}\tag{2}
$$
式2中$q(\theta)$为学习的参数分布，而$p(\theta)$为预先定义的先验分布。

在BBB中提升正则化

在BBB中KL正则化项对约束参数分布非常重要。理想上，$KL[q(\theta)\vert p(\theta)]$应该被最小化，从而确保$q(\theta)$与$p(\theta)$相近。然而，若每个参数的后验均值$\mu_i$与$0$的距离很远，那么KL项变得很大，若KL项过度正则化，那么会导致网络的表达力大大降低。

然而，RL优化问题往往具有很大噪音梯度估计，那么这些噪音估计会被进一步被KL项混合。因此，若在RL训练中应用BBB，往往会把KL项抛弃掉，也会导致每个部分的标准差往往为0。

信噪比约束的参数不确定性

为了缓和正则化和BBB网络高效训练的挑战，同时维持鲁棒性训练和网络泛化性，作者们提出了基于信噪比的正则化方法。该方法可确保模型拥有足够的随机性，且不会导致训练风险的坍塌。参数特定的信噪比为
$$
\begin{aligned}
\Omega_{SNR_i}=\frac{\vert\mu_i\vert}{\sigma_i}
\end{aligned}\tag{3}
$$
其中$\mu_i$表示网络参数的均值，$\sigma_i$表示网络参数的方差。

信噪比越高，表示参数的不确定性很少，导致更确定性的行为。然而，往往表示着对训练数据的过拟合。相反的，信噪比越低，表示更宽的概率分布和扁平的损失地图，从而提高泛化性。

为了控制参数的信噪比，作者们引入了一个正则化项，从而惩罚过高的信噪比。
$$
\begin{aligned}
\mathcal{L}^{SNR}=\sum_i[max(\Omega_{SNR_i}-\Omega_{Max SNR}, 0)]^2
\end{aligned}\tag{4}
$$
式(4)中$\Omega_{MaxSNR}$为预定义的信噪比上界。

接下来，讨论一下信噪比与KL-Divergence的关系
$$
\begin{aligned}
KL[q\Vert p] & = \frac{1}{2}[\frac{(\mu_q-\mu_p)^2}{\sigma_p^2}+\frac{\sigma_q^2}{\sigma_p^2}-1+ln(\frac{\sigma_p^2}{\sigma_q^2})] \\
& \stackrel{\mathrm{\sigma_p=\sigma_q}}{=}\frac{1}{2}[\frac{\vert\mu_q-\mu_p\vert}{\sigma_p}]^2 \\
& \stackrel{\mathrm{\mu_p\mu_q\gt0}}{=}\frac{1}{2}[\frac{\vert\mu_q\vert}{\sigma_q}-\frac{\vert\mu_p\vert}{\sigma_p}]^2 \\
& =\frac{1}{2}[\Omega_{SNR_q}-\Omega_{Max~SNR}]^2=\frac{1}{2}[\mathcal{L}^{SNR}(q)]
\end{aligned}\tag{5}
$$
该等式表示信噪比为简化的KL-Divergence。

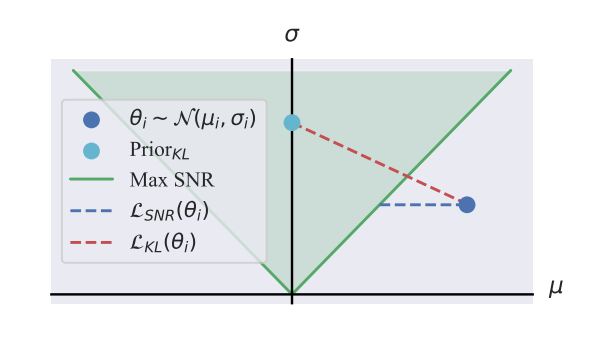
图1 KL-Divergence与SNR对参数分布的正则化效果

如图1所示，标准KL项往往把参数分布约束在0均值的高斯分布。然而，SNR允许更宽的参数分布，那么就可允许不仅仅寻找到对当前损失最优的解决方案，也能对参数空间的变化产生影响。

训练方法

若把SNR与PPO相整合，那么损失函数为
$$
\begin{aligned}
\mathcal{L}_t^{PPO+SNR}(\theta)=\underset{t}{\mathbb{E}}[\mathcal{L}_t^{CLIP}(\theta)-c_1\mathcal{L}_T^{VF}(\theta)]+c_2\mathcal{L}^{SNR}
\end{aligned}\tag{6}
$$

采样策略：与经典方法中每次rollout采样一次参数不如，作者们采用每个时间步随机模型参数的连续性重采样策略。该方法引入了更高的随机性，因此提升了模型在各种场景中的适应能力和鲁棒性。标准的PPO算法，利用熵奖励鼓励模型探索，阻止过度确定性的策略，而连续性重采样本质上使策略的拥有更少的确定性，因此损失函数中移除了熵奖励。

稳定化优势估计：由于信噪比约束的PUN用于高估的不确定性，那么高估随机网络架构会导致训练的不稳定性。因此，作者们对critic网络设定了确定性网络，而SNR约束的PNU为actor。

网络初始化：对于每个参数的$\mu_i,\sigma_i$初始化为：每个$\mu_i$从$\mathcal{U}(-\sqrt{\frac{2}{p}},\sqrt{\frac{2}{p}})$，且$p$为每个线性层的输入数量。$\sigma_i$从$\mathcal{U}(\sigma_{min},\sigma_{max})$中采样。其中，$\sigma_{min},\sigma_{max}$为可调节超参数。确切的说，作者们对$\sigma_{min},\sigma_{max}$进行了超参数搜索，与Noise Network相比，更大。同时，作者们发现用于初始化的高$\sigma$值会产生更好的泛化性结果。