浅谈状态空间模型SSM基础理论

状态空间模型是一个描绘系统随时间变化的动态行为，被广泛应用在控制理论、机器人、以及经济学。状态空间模型通过一系列隐藏变量，被称为“状态”，高效的捕获时序数据的依赖关系，从而具象化形态的行为。确切的说，状态空间模型由两种方程构成，分别是：状态方程和观测方程，从而构建时刻$t$输入$x(t)\in\mathbb{R}$和输出$y(t)\in\mathbb{R}$的关系。其中，隐藏状态$h(t)\in\mathbb{R}^N$的维度为$N$。
$$
\begin{aligned}
{h}'(t)=\mathbf{A}h(t)+\mathbf{B}x(t)
\end{aligned}\tag{1}
$$

$$
\begin{aligned}
y(t)=\mathbf{C}h(t)+\mathbf{D}x(t)
\end{aligned}\tag{2}
$$

${h}'(t)$为当前状态$h(t)$的导数，$\mathbf{A}\in\mathbb{R}^{N\times N}$为状态转换矩阵，用于状态随时间变化情况；$\mathbf{B}\in\mathbb{R}^{N\times1}$为输入矩阵，控制输入对状态的影响；$\mathbf{C}\in\mathbb{R}^{1\times N}$为输出矩阵，表示基于当前状态产生的输出；$\mathbf{D}$表示命令系数，决定输入对输出产生的直接影响。通常来说，大部分状态空间模型的$\mathbf{D}x(t)=0$，在深度学习可识别为skip连接。

离散化

为了满足各种各样真实世界场景中机器学习的需求，SSMs模型必须要经历离散化过程，把连续参数转换为离散参数。离散化方法通常把连续时间分为$K$个离散化间隔。其中，最有表示性的解决方案是Zero-Order Hold，其假设在间隔$[t_{k-1},t_k]$为常量。在ZOH离散化后，状态空间模型为
$$
\begin{aligned}
h_k=\bar{\mathbf{A}}h_{k-1}+\bar{B}x_k
\end{aligned}\tag{3}
$$

$$
\begin{aligned}
y_k=\mathbf{C}h_k
\end{aligned}\tag{4}
$$

其中，$\bar{\mathbf{A}}=exp(\Delta\mathbf{A})$,$\bar{\mathbf{B}}=(\Delta\mathbf{A})^{-1}(exp(\Delta A)-I)\cdot\Delta\mathbf{B}$，$k$为离散化时间步。由此可见，离散化SSMs与RNN拥有相似结构。因此，与自回归解码的Transformer相比，SSMs的推理很高效。

卷积运算

离散化状态空间模型属于一个线性系统，拥有相关特性，且与卷积运算无缝集成。确切的说，每个时间步可独立的计算输出
$$
\begin{aligned}
y_0=\mathbf{C}\bar{\mathbf{A}}^0\bar{\mathbf{B}}x_0
\end{aligned}\tag{5}
$$

$$
\begin{aligned}
y_1=\mathbf{C}\bar{\mathbf{A}}^1\bar{\mathbf{B}}x_0+\mathbf{C}\bar{\mathbf{A}}^0\bar{\mathbf{B}}x_1
\end{aligned}\tag{6}
$$

$$
\begin{aligned}
y_2=\mathbf{C}\bar{\mathbf{A}}^2\bar{\mathbf{B}}x_0+\mathbf{C}\bar{\mathbf{A}}^1\bar{\mathbf{B}}x_1+\mathbf{C}\bar{\mathbf{A}}^0\bar{\mathbf{B}}x_2
\end{aligned}\tag{7}
$$

$$
\begin{aligned}
\cdots
\end{aligned}\tag{8}
$$

$$
\begin{aligned}
y_2=\mathbf{C}\bar{\mathbf{A}}^k\bar{\mathbf{B}}x_0+\mathbf{C}\bar{\mathbf{A}}^{k-1}\bar{\mathbf{B}}x_1+\ldots+\mathbf{C}\bar{\mathbf{A}}^1\bar{\mathbf{B}}x_{k-1}+\mathbf{C}\bar{\mathbf{A}}^0\bar{\mathbf{B}}x_k
\end{aligned}\tag{9}
$$

通过创建卷积核$\bar{\mathbf{K}}=(\mathbf{C}\bar{\mathbf{B}},\ldots,\mathbf{C}\bar{\mathbf{A}}^{k}\bar{\mathbf{B}},\ldots)$，循环计算可转化为卷积形式
$$
\begin{aligned}
y=\mathbf{x}*\mathbf{\bar{K}}
\end{aligned}\tag{10}
$$
其中，$\mathbf{x}=[x_0,x_1,\ldots]$和$\mathbf{y}=[y_0,y_1,\ldots]\in R^{L}$表示输入和输出序列，$L$为序列长度。卷积运算使SSMs模型可充分利用现代矩阵运算硬件，从而在训练过程中实现并行计算，这对于利用非线性激活函数的RNN不可能。这种情况下给定$D$维输入$x(k)$，SSMs模型独立的计算每一个维度，最终产生$D$维度输出$y(t)$。在这种情况下，输入矩阵、输出矩阵、命令矩阵、以及状态转换矩阵均保持不变。

RNN,Transformer,以及SSM之间的关系

RNN,Transformer,以及SSM之间的关系，可见图2所示。

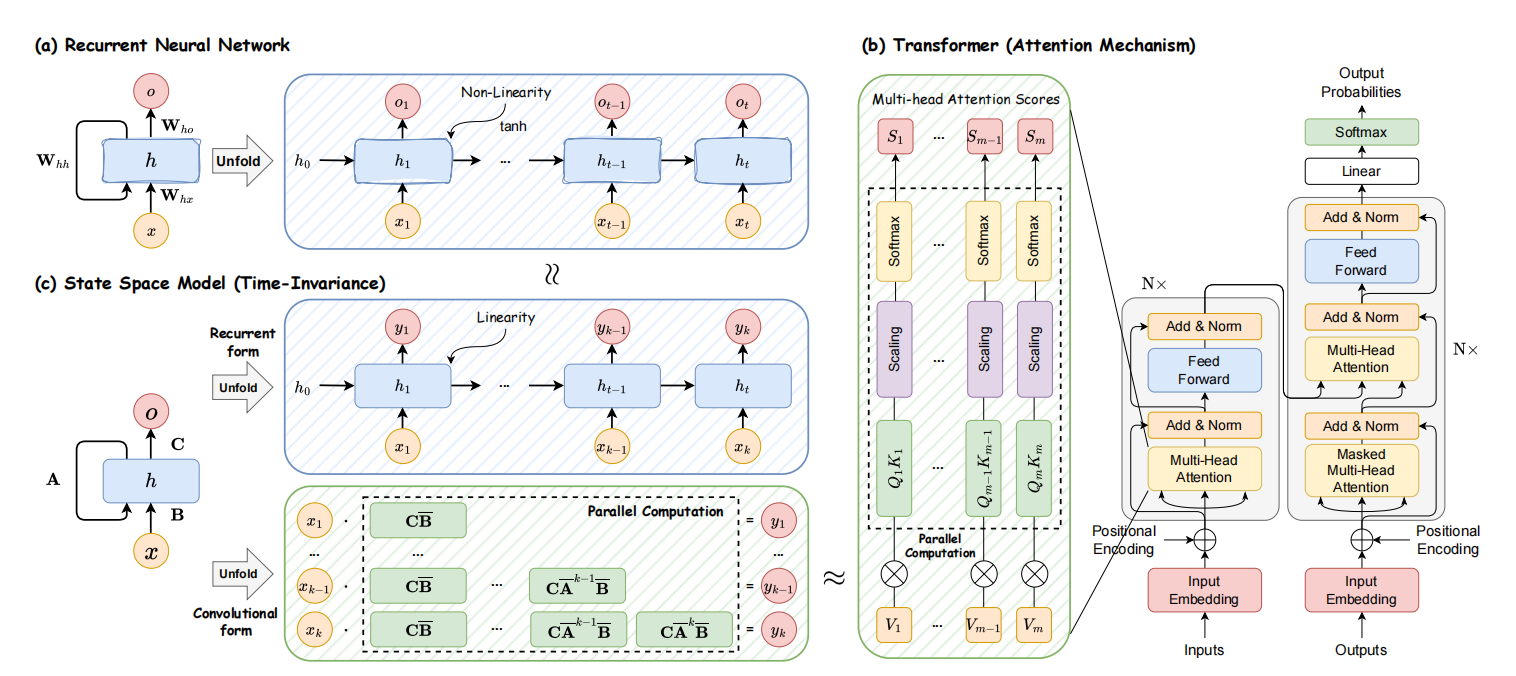
图1 模型架构的描述

RNN在非线形循环框架下计算，且每个计算只取决于之前的隐藏状态和当前输入。虽然这种方式导致RNN可快速的推理，但是阻碍了利用GPU并行计算的能力，即训练缓慢。与之相比，Transformer的推理过程很缓慢。这是因为语言模型的自回归设计导致每个输出的计算，均需要重复计算注意力分数。与RNN和Transformer模型相比，离散化SSMs支持循环运算和卷积运算，即不仅可高效推理也可高效计算。然而，经典的SSMs模型属于时间不变的，即$A,B,C$以及$\Delta$与模型输入无关。这限制了上下文意识的建模，从而导致SSMs在特定任务用于次优表现，例如：选择性复制。

确切的说，状态空间模型模型拥有广泛的意义，只表示具有任何隐式状态的循环过程的概念。在许多学科中，用于指代其它概念，包含马尔可夫决策过程、卡尔曼滤波、动力学因果建模、隐马尔可夫模型、线性动力学系统、以及深度学习中循环神经网络。