AlphaGo技术细节
完全信息的博弈或游戏均有最优的价值函数${v}^{*}(s)$,例如:象棋、围棋、西洋双陆棋、以及拼字游戏,也均可迭代地计算最优价值函数解决。然而,由于游戏的搜索空间差别很大,从而导致解决的难度不同。若利用$b$表示游戏的宽度(每个位置可移动的方向)和$f$表示深度(游戏的长度),那么象棋$b\approx35,d\approx80$与围棋$b\approx250,d\approx150$,对应的搜索空间均为$b^d$。为了降低搜索空间,有两种办法,第一种通过位置评估减少搜索的深度,即把搜索树中状态$s$的子树利用价值函数$v(s)\approx {v}^{*}(s)$替换。这种方法很好的解决了象棋和西洋跳棋问题,但对搜索空间巨大的围棋问题没有得到很好的解决。第二种方法是减少搜索的广度可通过从策略$p(a\vert s)$中采样动作的方式实现,这种方式在西洋双陆棋和拼字游戏中实现了卓越性能,在围棋Go游戏只达到了弱初级选择级别。
在AlphaGo之前,对于围棋问题,主要通过MCTS算法执行MC roolouts方式估计搜索树中每个状态的价值,从而缩小搜索空间,且实现了较强的初级选择级别。这些方法主要受限于策略或价值函数只是输入特征的线性组合。AlphaGo利用卷积神经网络提取棋盘图像的低维表示的能力,作为策略网络和价值网络的特征提取器。如图1所示,网络的训练由机器学习的许多阶段构成。
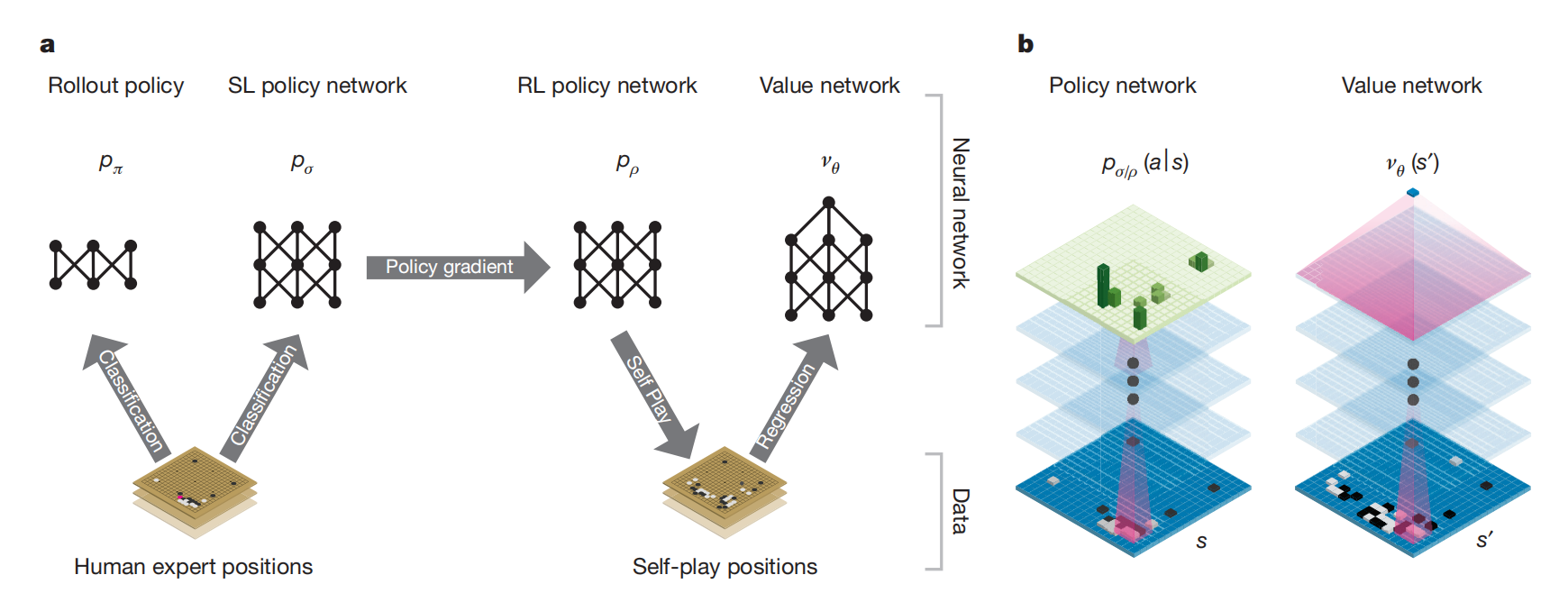
图1 网络架构与训练流程。a,网络训练流程;b,网络架构的原理图。
首先,作者们训练监督学习训练SL策略$p_{\sigma}$,以利用即时反馈和高质量梯度提供快速且高效的学习更新。同时,训练了一个快策略$p_{\pi}$,用于rollouts进行快速采样动作。接下来,训练了一个RL策略$p_{\rho}$,通过self-play的方式提升优化SL策略。这种方式有利用纠正博弈的目标。最后,作者们训练价值网络用于预测两个玩家执行位置$s$产生的结果。总的来说,AlphaGo高效的集合了策略网络和利用MCTS的价值网络。
| 特征 | 网络架构 | 目标 | 性能 | |
|---|---|---|---|---|
| 监督学习策略网络 | 人为构造(非图像) | 13层卷积网络,ReLu为激活函数 | MLE | acc:57% 11%(vs Pachi);12%(Fuego) |
| rollout策略 | 人为提取的小模式特征 | 线性softmax函数 | MLE | acc:24.2% |
| RL策略网络 | 图像 | 13层卷积网络,Relu为激活函数 | 最大化期望回报 | 80%(vs SL策略);85%(vs Pachi策略) |
| RL价值网络 | 图像 | 13层卷积网络,Relu为激活函数;输出的维度为1 | MSE(回归状态-结果对) | 接近于RL策略的MC Rollouts的acc |
其中,RL策略网络的初始化与监督学习策略一致。在与环境交互阶段,利用当前策略与随机选择SL策略的版本,两者交替获取动作,即自博弈。随机选择SL策略的版本有利于降低对当前对手策略过拟合的风险。其中,奖励函数在非终止状态为0,而终止状态时胜利为1,否则为-1。
在价值网络训练时,利用一整个完整游戏过程的数据往往导致过拟合,这是因为连续位置之间有很强的相关性。为了缓解该问题,作者们利用由3千万位置不同的self-play数据集训练,每一个位置采样于一个独立的游戏。每个游戏是RL策略与自身进行博弈。
利用价值网络和策略进行搜索
如图2所示,AlphaGo在MCTS算法中集合策略网络和价值网络,通过向前搜索的方式选择动作。
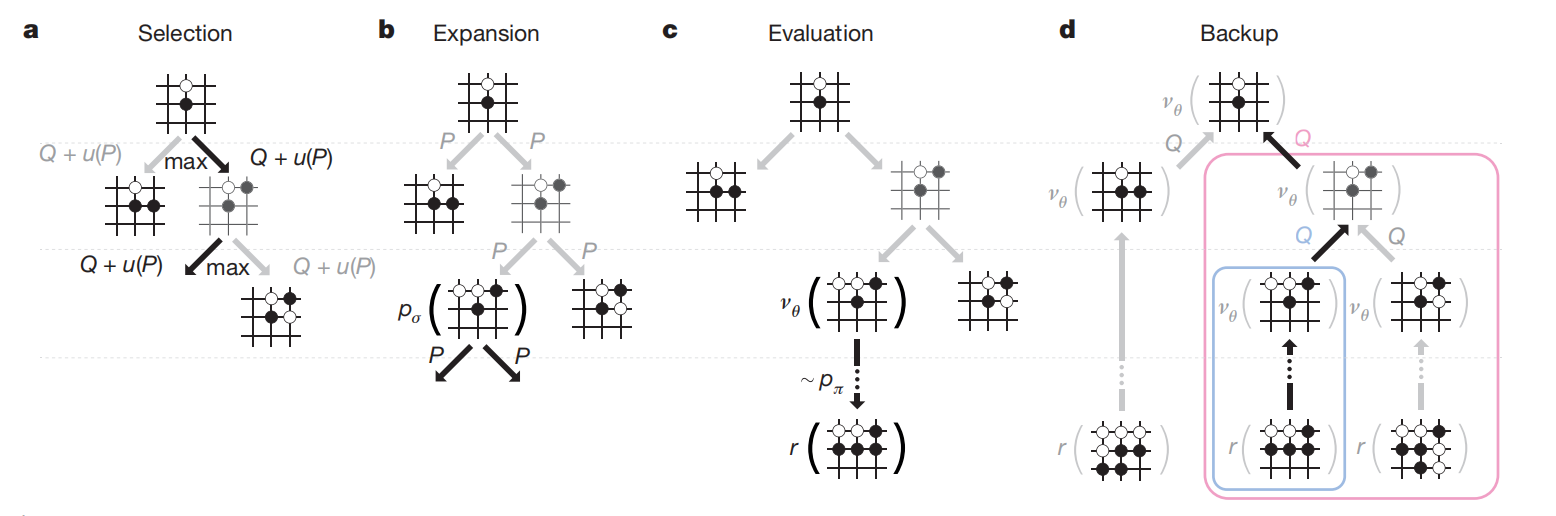
图2 AlphaGo中的MCTS
搜索树的每条边存储价值$Q(s,a)$、访问次数$N(s,a)$、以及先验概率$P(s,a)$。从根节点开始,向下搜索的方式遍历树。
动作选择
每个模拟的每个时间步,从状态$s_t$选择动作$a_t$
$$
\begin{aligned}
a_t=\underset{a}{argmax}(Q(s_t,a)+u(s_t,a))
\end{aligned}\tag{1}
$$
其中,
$$
\begin{aligned}
u(s,a)\propto\frac{P(s,a)}{1+N(s,a)}
\end{aligned}\tag{2}
$$
$u(s,a)$与先验概率呈正比,与$N(s,a)$访问次数呈现反比以鼓励探索。
叶节点展开与评估
若在步骤$L$达到叶节点$s_L$,那么叶节点可能被展开。叶位置$s_L$只会被SL策略网络$p_{\sigma}$处理一次,对于每个输出的合法动作$a$的概率被存储为先验$P(s,a)=p_{\sigma}(a\vert s)$。叶节点可被两种不同的方式评估,第一种是通过价值网络$v_{\theta}(s_L)$;第二种是利用快速rollout策略$p_{\pi}$执行rollout直到终止步骤$T$。因此,作者们结合两者作为评估
$$
\begin{aligned}
V(s_L)=(1-\lambda)v_{\theta}(s_L)+\lambda z_L
\end{aligned}\tag{3}
$$
在模拟的结束,动作价值与所有遍历边的访问次数被更新。每个边累积访问次数与所有模拟评估的均值,即
$$
\begin{aligned}
N(s,a)=\sum_{i=1}^n 1(s,a,i)
\end{aligned}\tag{4}
$$
$$
\begin{aligned}
Q(s,a)=\frac{1}{N(s,a)}\sum_{i=1}^n 1(s,a,i)V(s_L^i)
\end{aligned}\tag{5}
$$
式中$s_L^i$为第$i$次模拟叶节点,$i(s,a,i)$表示边$(s,a)$是否被访问。
值得注意的是,SL策略性能优越于RL策略,这是因为人选择各种各样有前景的移动,而$RL$只选择最优的。基于RL策略学习的价值函数性能优于SL策略。
最后,作者们为高效的结合MCTS与策略网络,因此使用了异步的多线程。
引用方法
请参考:
li,wanye. "AlphaGo技术细节". wyli'Blog (Sep 2024). https://www.robotech.ink/index.php/archives/619.html
或BibTex方式引用:
@online{eaiStar-619,
title={AlphaGo技术细节},
author={li,wanye},
year={2024},
month={Sep},
url="https://www.robotech.ink/index.php/archives/619.html"
}
怎么收藏这篇文章?
可以通过收藏公众号对应文章的方式收藏,谢谢支持