Score-SDE：基于随机微分方程的分数估计扩散模型

扩散模型是一类概率生成模型，它通过注入噪声逐步破坏数据，然后学习其逆过程，以生成样本。目前，扩散模型主要有三种形式：去噪扩散概率模型[2,3] (Denoising Diffusion Probabilistic Models, 简称DDPMs)、基于分数的生成模型[4,5] (Score-Based Generative Models,简称SGMs)、基于随机微分方程估计分数的模型[6,7,8] (Stochastic Differential Equations,简称Score SDEs)。

Score SDEs

DDPM和SGM扩散模型均遵循一个统一的范式：首先利用高斯噪音扰动数据使原始数据分布与标准正态分布一致；然后，从标准正态分布的数据抽样，利用朗之万MCMC抽样法，生成原始数据。与之相比，文献[6]Score SDE(Stochastic Differential Equation)模型利用随机微分方程扩展到无限噪音规模，其扩散过程被建模为$It\hat{o}$随机微分方程的解，可见式(1)。
$$
\begin{aligned}
d\mathbf{x}=\mathbf{f}(\mathbf{x},t)dt + g(t)d\mathbf{w}
\end{aligned}\tag{1}
$$
式(1)中，$\mathbf{w}$为标准维纳过程，也就是布朗运动；$\mathbf{f}(\cdot,t):\mathbb{R}^d\to\mathbb{R}^d$是一个值为向量的函数，被称为$\mathbf{x}(t)$的漂移系数；$g(\cdot):\mathbb{R}\to\mathbb{R}$是一个标量函数，被称为$\mathbf{x}(t)$的扩散系数。根据文献[12]，可知，只要飘逸系数和扩散系数满足Lipschitz连续，那么随机微分方程的强解一定存在。同时，$\mathbf{x}(t)$的概率密度函数用$p_t(\mathbf{x})$表示；对于$0\le s\lt t\le T$，$p_{st}(\mathbf{x}(t)\vert\mathbf{x}(s))$表示从$\mathbf{x}(s)$转换到$\mathbf{x}(t)$。

DDPM和SGM可被视为两个不同SDEs的离散化。其中，SGM扩散过程对应的随机微分方程为$d\mathbf{x}=\sqrt{\frac{d[\sigma^2(t)]}{dt}}d\mathbf{w}$；DDPM扩散过程对应的随机微分方程为$d\mathbf{x}=-\frac{1}{2}\beta(t)\mathbf{x}dt+\sqrt{\beta(t)}d\mathbf{w}$。对于SGM的微分方程，随着$t\to\infty$，产生一个方差爆炸的随机过程，因此对应的随机微分方程被称为"VE-SDE"；对于DDPM的随机微分方程，随着$t\to\infty$，产生方差为1的随机过程，因此对应的随机微分方程被称为"VP-SDE"。

根据文献[6]，可知，扩散过程的逆过程也是一个扩散过程，其反向时间随机微分方程可见式(2)
$$
\begin{aligned}
d\mathbf{x}=[\mathbf{f}(\mathbf{x},t)-g(t)^2\nabla_{\mathbf{x}}log{p_t(\mathbf{x})}]dt+g(t)d\mathbf{\bar{w}}
\end{aligned}\tag{2}
$$
式(2)中$\mathbf{\bar{w}}$为时间反向的标准维纳过程，$dt$为无穷小的负的时间步长。

只要式(2)中$\nabla_{\mathbf{x}}log{p_{t}(\mathbf{x})}$对于所有时间$t$已知，那么就可以根据式(2)推导逆扩散过程，从而生成样本。

如图4所示，Score SDEs扩散过程和逆扩散过程示意图。

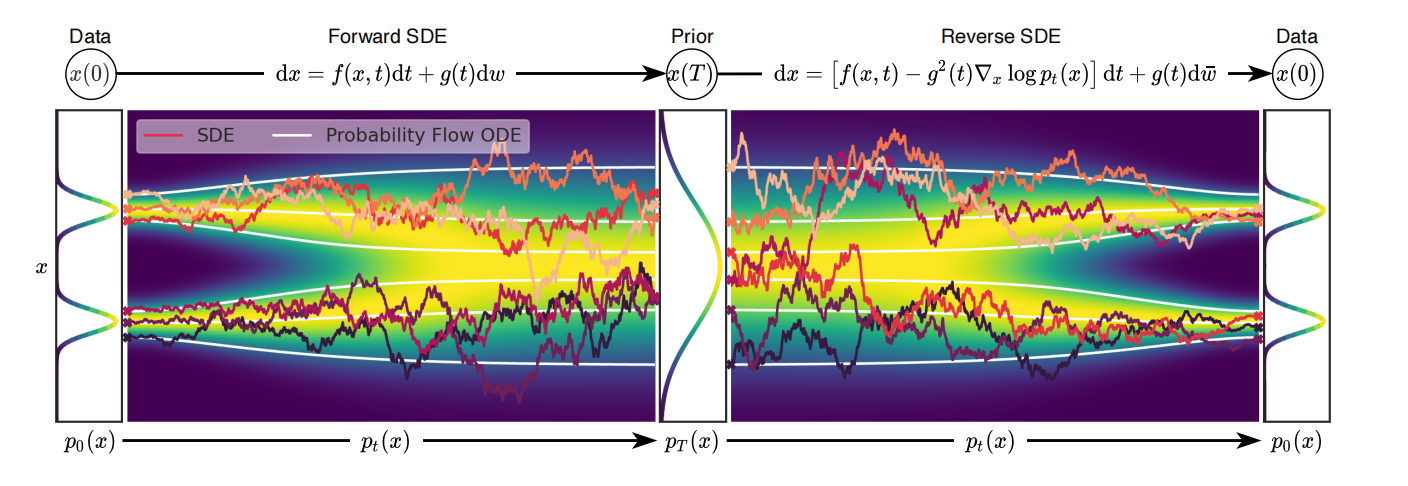
图(4)中$\mathbf{x}(0)\sim p_0$表示样本数据；$\mathbf{x}(T)\sim p_T$表示先验分布，不包含$p_0$的任何信息，例如：高斯分布。

随机微分方程的分数估计

与DDPMs和SDMs一样，训练一个与时间依赖的分数模型$\mathbf{s_{\theta}}(\mathbf{x},t)$估计分数$\nabla_\mathbf{x}log{p_t(\mathbf{x})}$，可见式(3)
$$
\begin{aligned}
\theta^{*}=\underset{\theta}{argmin}\mathbb{E}_{t}\{\lambda(t)\mathbb{E}_{\mathbf{x}(0)}\mathbb{E}_{\mathbf{x}(t)\vert\mathbf{x}(0)}[\Vert\mathbf{s}_{\theta}(\mathbf{x}(t),t)-\nabla_{\mathbf{x}(t)}log{p_{0t}(\mathbf{x}(t)\vert\mathbf{x}(0))}\Vert_2^2]\}
\end{aligned}\tag{3}
$$
式(3)中$\lambda:[0,T]\to\mathbb{R}_{\gt0}$是一个正权重函数。与DDPMs和SDMs一样，$\lambda\propto\frac{1}{\mathbb{E}[\Vert\nabla_{\mathbf{x}(t)}log{p_{0t}(\mathbf{x}(t)\vert\mathbf{x}(0))}\Vert^2_2]}$

若转换函数$p_{0t}(\mathbf{x}(t)\vert\mathbf{x}(0))$已知，那么式(3)便高效可解。若函数$\mathbf{f}(\cdot,t)$为防射函数，以及转换函数为高斯分布，那么均值和方差可知，从而分数估计网络可训练。

样本生成

分数估计网络训练完成后，可利用数值SDE求解器求解反向时间随机微分方程。数值求解器提供了随机微分方程的近似求解器，例如：Euler-Maruyama和随机Runge-Kutta方法。为了提高采样质量，利用数值SDE求解器得到下一时刻$t$的样本估计$\mathbf{x}_t$，再利用基于分数的MCMC方法纠正$\mathbf{x}_t$，即数值SDE求解器扮演“预测器”的角色，MCMC方法扮演“纠正器”的角色，该方法被称为Predictor-Corrector采样。

黑盒常微分方程求解器

对于所有的扩散过程，均有一个对应的确定过程，即它的轨迹与随机微分方程共享相同的概率密度$\{p_t(\mathbf{x})\}_{t=0}^T$。确定过程满足的ODE(Ordinary Differential Equation)为
$$
\begin{aligned}
d\mathbf{x}=[\mathbf{f}(\mathbf{x},t)-\frac{1}{2}g(t)^2\nabla_{\mathbf{x}}log{p_{t}(\mathbf{x})}]dt
\end{aligned}\tag{4}
$$
只要分数$\nabla_{\mathbf{x}}log{p_{t}}(\mathbf{x})$已知，那么式(4)就可以被确定，该常微分方程被称为概率流ODE。那么，求解该常微分方程就可以进行采样。因为利用神经网络估计分数，所以该方法被称为黑盒常微分方程求解器。

条件扩散模型

利用随机微分方程把扩散模型扩展到连续结构，不仅允许从$p_0$采样生成数据样本，而且允许基于条件的生成$p_0(\mathbf{x}(0)\vert\mathbf{y})$。给定扩散过程随机微分方程(1)，可从$p_t(\mathbf{x}(t)\vert\mathbf{y})$采样，其逆扩散过程随机微分方程为
$$
\begin{aligned}
d\mathbf{x}=\{\mathbf{f}(\mathbf{x},t)-g(t)^2[\nabla_{\mathbf{x}}log{p_t(\mathbf{x})}+\nabla_{\mathbf{x}}log{p_{t}(\mathbf{y}\vert\mathbf{x})}]\}dt+g(t)d\mathbf{\bar{w}}
\end{aligned}\tag{5}
$$
根据式(5)，可知，只要给定扩散过程梯度的估计$\nabla_{\mathbf{x}}log{p_t(\mathbf{y}\vert\mathbf{x}(t))}$，那么就可以求解逆问题的随机微分方程。可通过训练一个模型估计扩散过程$p_t(\mathbf{y}\vert\mathbf{x}(t))$，也可以利用启发式方法和领域知识估计其梯度。

参考文献

[1] Yang L, Zhang Z, Song Y, et al. Diffusion models: A comprehensive survey of methods and applications[J]. ACM Computing Surveys, 2023, 56(4): 1-39.

[2] Ho J, Jain A, Abbeel P. Denoising diffusion probabilistic models[J]. Advances in neural information processing systems, 2020, 33: 6840-6851.

[3] Sohl-Dickstein J, Weiss E, Maheswaranathan N, et al. Deep unsupervised learning using nonequilibrium thermodynamics[C]//International conference on machine learning. PMLR, 2015: 2256-2265.

[4] Song Y, Ermon S. Generative modeling by estimating gradients of the data distribution[J]. Advances in neural information processing systems, 2019, 32.

[5] Song Y, Ermon S. Improved techniques for training score-based generative models[J]. Advances in neural information processing systems, 2020, 33: 12438-12448.

[6] Song Y, Sohl-Dickstein J, Kingma D P, et al. Score-based generative modeling through stochastic differential equations[J]. arXiv preprint arXiv:2011.13456, 2020.

[7] Song Y, Durkan C, Murray I, et al. Maximum likelihood training of score-based diffusion models[J]. Advances in Neural Information Processing Systems, 2021, 34: 1415-1428.

[8] Karras T, Aittala M, Aila T, et al. Elucidating the design space of diffusion-based generative models[J]. Advances in Neural Information Processing Systems, 2022, 35: 26565-26577.

[9] Rao–Blackwell theorem - Wikipedia

[10] Evidence lower bound - Wikipedia

[11] Generative Modeling by Estimating Gradients of the Data Distribution | Yang Song (yang-song.net)

[12] Itô diffusion - Wikipedia