SDQN：连续性动作的离散化序列预测

连续空间的控制问题一致很难被有效解决，这是因为动作空间每个维度的离散化会导致动作的组合呈指数级爆炸。正是这样的问题，也导致DQN算法无法应用于连续动作空间，主要的原因是该算法$Q$函数更新的损失函数为式(1)
$$
\begin{equation}
L=\mathbb{E}_{\mathbf{s}_t\sim\rho_{\beta}(\cdot),\mathbf{s}_{t+1}\sim\rho_{\xi}(\cdot\vert\mathbf{s}_t,\mathbf{a}_t)}\Vert Q(\mathbf{s}_t,\mathbf{a}_t)-(r+\gamma Q(\mathbf{s}_{t+1},argmax_{a_{t+1}}Q(\mathbf{s}_{t+1},\mathbf{a}_{t+1})))\Vert^2
\end{equation}\tag{1}
$$
根据式(1)，可知，DQN的目标函数需要求下一时刻状态$\mathbf{s}_{t+1}$下使$Q$值最大的动作，即为off-policy算法。这对于连续动作空间，最大化是很难求的。

为了处理连续动作空间的问题，DDPG基于DPG理论直接学习了一个策略网络，该策略网络的目的就是给定状态$s_t$输出价值最大化的动作$a_t$，即训练了两个网络分别是$Q$网络和策略网络。

与DDPG不同，SDQN采用了一种与众不同的方法，它把动作空间维度为$N$的原始MDP分解为包含序列一维的相似MDP，如图1所示。

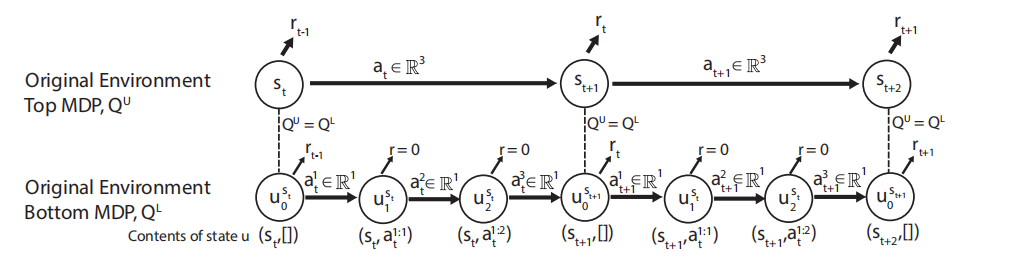
根据图1，可知，两层MDP均对环境建模。下层MDP中状态$u_{k}^{s_t}=(s_t,a^{1:k})$，即为状态$s_t$下执行下层动作$a^1\cdots a^k$之后的状态；上层动作$a^t$为下层动作$a^{1:N}$的组合，即下层的动作表示动作空间中一个维度的动作。对于环境来说，执行动作$a_t$才会导致环境状态发生变化。

为了保证上层MDP下的$Q(s_t,a_t)$与下层MDP下的$Q(u_{0}^{s_t},a_{t}^{1:N})$值一致，因此对于下层MDP中执行动作$a^{1:N-1}_t$的奖励为0，对应的折扣系数$\gamma$也为0。

这种建模方式需要训练两个$Q$网络，分别为$Q^U$和$Q^L$。对于$Q^U$网络，利用TD-0学习方法，其目标函数式(2)
$$
\begin{equation}
l_{td}=\mathbb{E}_{(\mathbf{s}_t,\mathbf{a}_t,\mathbf{s}_{t+1})\in R}[(r+\gamma Q^{U}(s_{t+1},\pi(s_{t+1}))-Q^U(s_t,a_t))^2]
\end{equation}\tag{2}
$$
对于$Q^L$网络，在$k<N$时，目标函数为式(3)
$$
\begin{equation}
l_{inner}=\mathbb{E}_{\mathbf{s},\mathbf{a}\in R}\sum_{k=1}^{N-1}[Q^L(\mathbf{u}^\mathbf{s}_{k-1},a^k)-\underset{a^{k+1}\in\mathcal{A}^{k+1}}{max}Q^{L}(\mathcal{u}^\mathcal{s},a^{k+1})^2]
\end{equation}\tag{3}
$$
对于$k=N$时，目标函数为式(4)
$$
\begin{equation}
l_{base}=\mathbb{E}_{(\mathbf{s},\mathbf{a})\in R}[Q^U(\mathcal{s},\mathcal{a})-Q^{L}((\mathcal{s},\mathcal{a}^{1:N-1}),a^N))]^2
\end{equation}\tag{4}
$$
由此可见，这种方式可以通过$Q$函数最大化的方式设定目标值。与DQN相似，模型训练时也采用了目标网络和replay-memory buffer降低数据之间的相关性。确切的说，SDQN的采样与训练，可见算法1和算法2所示。