ABS:学习无碰撞高速运动
ABS是一款四足机器人在杂乱环境中敏捷且高速运动的全新框架。与利用线上系统识别和迁移学习方式实现快速运动的方式不同,该框架有两个策略:敏捷策略以实现执行敏捷电动机技能和恢复策略以保护机器人安全。训练过程包含敏捷策略学习、避碰价值网络、恢复策略学习、以及外部感知表示网络,这些网络在仿真环境中训练完成之后,直接部署到真实机器人上。其中,避碰价值网络主要作用是管理策略的切换。最终,该机器人能够实现高速运动,且可以躲避静态和动态障碍物的能力。如图1所示,ABS系统架构概览。
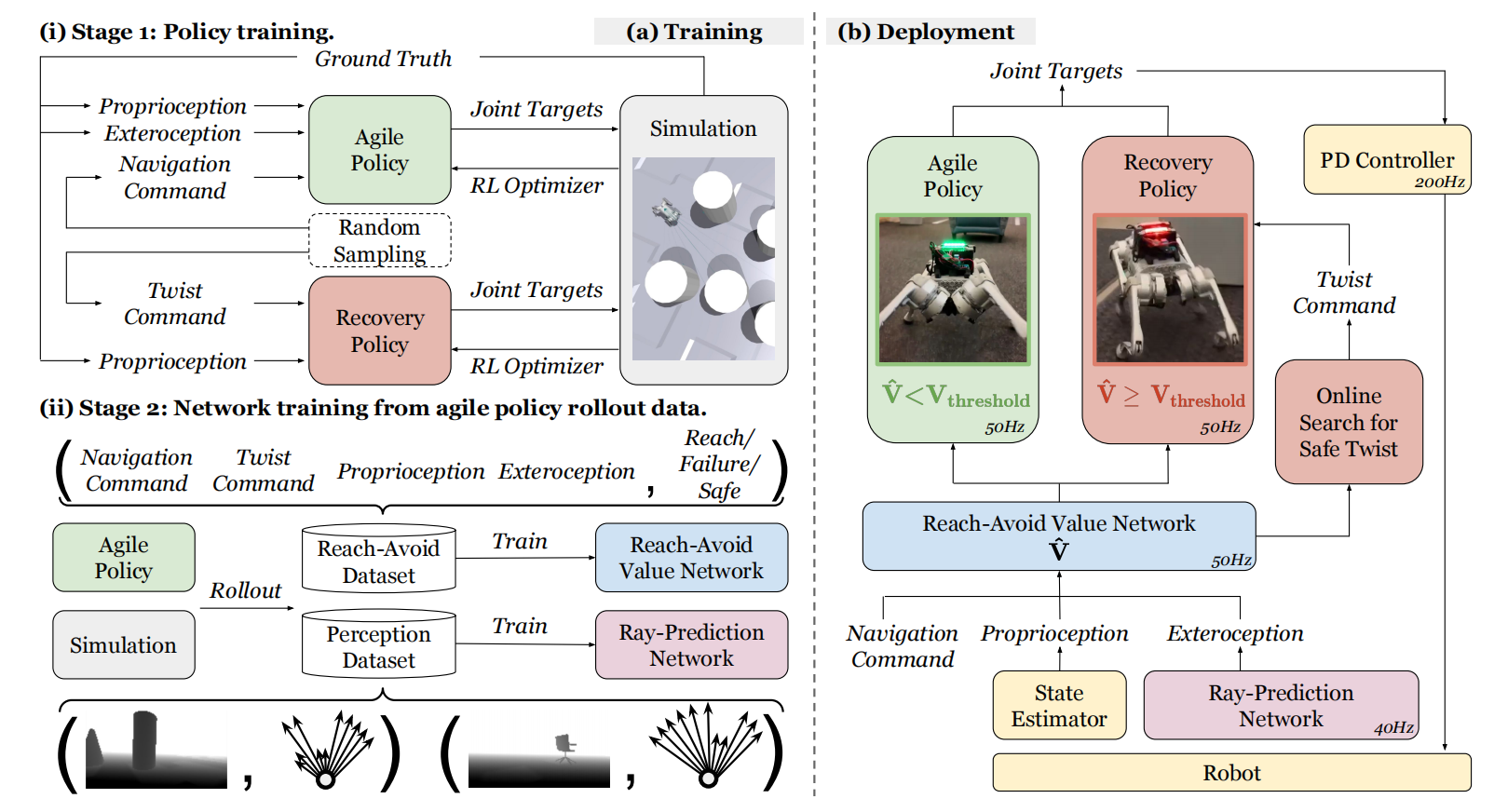
图1 ABS系统架构概览
敏捷策略的学习
之前的方式是以速度追踪的方式实现快速运动;ABS是以目标追踪的方式实现快速运动,两种方式的不同主要体现在奖励函数的设置上。
观测空间与动作空间
观测空间主要由脚接触点$c_{f\in\{1,2,3,4\}}$、基座角速度$w$、投影重力$g$、基座的目标命令$G^c$(目标的相对位置和方向)、episode剩下的时间$T-t$、关节位置$q$、关节速度$\dot{q}$、历史动作$a$、以及外部感知(距离的$log$值)$R$。其中,脚接触点就是脚与地面的接触点;投影重力是指重力在机器人动作空间的投影。观测空间中投影重力$g$由IMU传感器获取,目标命令$G^c$由里程计获取。动作空间就是机器人的12个关节的位置构成,其位置再被PD控制器转化为力矩。
总的来说,观测空间由本体感知、外部感知、历史动作构成。
奖励函数
奖励函数由三项构成,可见式(1)
$$
\begin{aligned}
r = r_{penalty}+r_{task}+r_{regularization}
\end{aligned}\tag{1}
$$
惩罚奖励主要惩罚碰撞,其奖励函数很直接:$r_{penalty}=-100\cdot\mathbb{1}(undesired\quad collision)$
任务奖励主要确保机器人以合适的朝向和姿势达到目标状态,可见式(2)
$$
\begin{aligned}
r_{task}=60\cdot r_{possoft}+60\cdot r_{postight}+30\cdot r_{heading} -10\cdot r_{stand}+10\cdot r_{agile}-20\cdot r_{stall}
\end{aligned}\tag{2}
$$
式(2)中$r_{possoft}$为软位置追踪项,$r_{postight}$为紧的位置追踪项,$r_{heading}$用于调节机器人方向接近目标。这三项的计算公式可见式(3)
$$
\begin{aligned}
r_{track(possoft/postight/heading)}=\frac{1}{1+\Vert\frac{error}{\sigma}\Vert^2}\cdot\frac{\mathbb{1}(t\gt T-T_r)}{T_r}
\end{aligned}\tag{3}
$$
对于软位置追踪$\sigma_{soft}=2m,T_r=2s$;对于硬的位置追踪项$\sigma_{tight}=0.5m,T_r=1s$;对于方向追踪项$\sigma_{heading}=1rad,T_r=2s$。
站立项的奖励被定义为
$$
\begin{aligned}
r_{stand}=\Vert q-\bar{q}\Vert_1\cdot\frac{\mathbb{1}(t\gt T-T_{r,stand})}{T_{r,stand}}\cdot\mathbb{1}(d_{goal}-\sigma_{tight})
\end{aligned}\tag{4}
$$
式(4)中$T_{r,stand}=1s$。
敏捷奖励被定义为
$$
\begin{aligned}
r_{agile}=max\{ReLU(\frac{v_x}{v_{max}})\cdot\mathbb{1}(correct\quad direction),\mathbb{1}(d_{goal}\lt\sigma_{tight})\}
\end{aligned}\tag{5}
$$
式(5)中$v_x$为基座前向速度,$v_{max}=4.5m/s$。"correct direction"是指机器人的方向和机器人与目标之间连线的夹角应该小于$105^{o}$。
若机器人在$d_{goal}\lt\sigma_{soft}$时保持静止且机器人不在"correct direction"时,静止奖励项$r_{stall}$为1,从而惩罚机器人浪费时间。
正则化奖励主要惩罚机器人不安全的状态,主要包括限位惩罚和与地面无接触惩罚,可见式(6)
$$
\begin{aligned}
r_{regularization}=-2\cdot v_z^2-0.05\cdot(w_x^2+w_y^2)-20\cdot(g_x^2+g_y^2)-0.0005\Vert\tau\Vert_2^2 \\
-20\cdot\sum_{i=1}^{12}ReLU(\vert\tau_i\vert-0.85\cdot\tau_{i,lim})-0.0005\cdot\Vert\dot{q}\Vert_2^2-20\cdot\sum_{i=1}^{12}ReLU(\vert\dot{q}\vert-0.9\cdot\dot{q}_{i,lim}) \\
-20\cdot\sum_{i=1}^{12}ReLU(\vert q_i\vert-0.95\cdot q_{i,lim})\\
-2\times 10^{-7}\cdot\Vert\ddot{q}\Vert_2^2-4\times10^{-6}\cdot\Vert\dot{a}\Vert_2^2-20\cdot\mathbb{1}(fly)
\end{aligned}\tag{6}
$$
模型训练
与其它工作一样,利用参数随机化使策略更鲁棒。同时,作者把领域随机化分为三大类,分别是:观测参数、动力学参数、以及episode参数。
表1 领域随机化设置
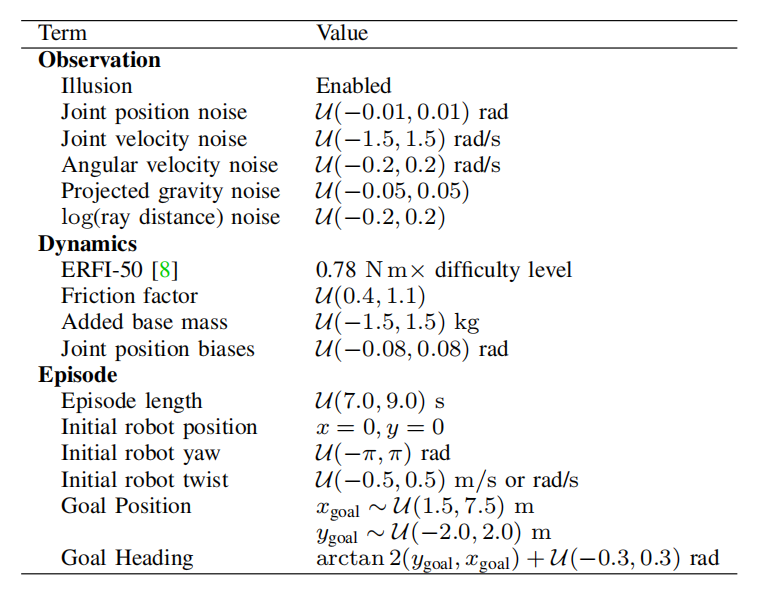
注: 根据自己的思考,观测参数是根据关节限位设置的;动力学参数可参照相关工作设置;episode参数需要根据经验调节。
避碰价值函数的学习与用法
价值函数的学习利用了避碰RL, 一种保障机器人安全且实现最优控制的学习方法。
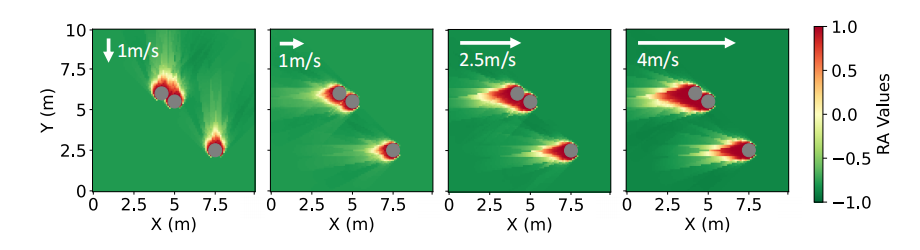
图2 RA价值函数可视化
RA价值函数
定义
若$\mathcal{F}\subseteq\mathcal{S}$为不安全状态,那么$\mathcal{F}$可利用Lipschitz连续函数$\zeta:\mathcal{S}\to\mathbb{R}$的零值子集定义,即$s\in\mathcal{F}\Leftrightarrow\zeta(s)\gt0$
若目标集合$\Theta\subseteq\mathcal{S}$为目标状态,那么目标状态可被表示为Lipschitz连续函数$l:\mathcal{S}\to\mathbb{R}$的零值子集表示,即$s\in\Theta\Leftrightarrow l(s)\le0$。
若策略$\pi$下状态$s_t$至$s_T$的未来轨迹表示为$\xi_{s_t}^{\pi}(\cdot)$,那么策略$\pi$下的reach-avoid集合定义为
$$
\begin{aligned}
\mathcal{RA}^{\pi}(\Theta;\mathcal{F}):=\{s_t\in\mathcal{S}\vert\xi_{s_t}^{\pi}(T-t)\in\Theta\land\forall{t}'\in[0,T-t],\xi_{s_t}^{\pi}({t}')\notin\mathcal{F}\}
\end{aligned}\tag{7}
$$
其中,$\xi_{s_t}^{\pi}(0)=s_t$
价值函数的学习
价值函数的观测空间由基座位置、目标位置和外部感知构成。
$$
\begin{aligned}
o^{RA}=[[v;w];G^c_{x,y};R]
\end{aligned}\tag{8}
$$
其损失函数为
$$
\begin{aligned}
L=\frac{1}{T}\sum_{t=1}^T(\hat{V}(o_t^{RA})-\hat{V}^{target})^2
\end{aligned}\tag{9}
$$
其中,$\hat{V}^{target}$为
$$
\begin{aligned}
\hat{V}^{target}=\gamma_{RA}max\{\zeta(s_t),min\{l(s_t),\hat{V}^{old}(o^{RA}_{t+1})\}\}\\
+(1-\gamma_{RA})max\{l(s_t),\zeta(s_t)\}
\end{aligned}\tag{10}
$$
式(9)中$\gamma_{RA}=0.999999$,从而使价值函数拟合至最优$V_{RA^*}^{\pi}(s)$;$\hat{V}^{old}$为之前迭代的价值函数,且设$\hat{V}^{old}(o^{RA}_{T+1})=+\infty$
根据目标函数可知,RA价值函数的学习是基于离线学习的方式,首先收集策略轨迹数据,然后训练RA价值函数。
实现
在RA价值函数学习中,$l(s)$与$\zeta(s)$被定义为
$$
\begin{aligned}
l(s)=tanh\quad log\frac{d_{goal}}{\sigma_{tight}}
\end{aligned}\tag{11}
$$
$$
\begin{aligned}
\zeta(s)=2*\mathbb{1}(undesired\quad collision) - 1
\end{aligned}\tag{12}
$$
由于式(12)违反了Lipschtiz连续,所以对$\zeta$函数进行了松弛。若碰撞发生,那么$\zeta$值将重新标记为$-0.8,-0.6,\ldots,0.8,1.0$,且持续10个时间步。
注:这一部分还是不太理解,若按照这样顺序持续10个时间步,那么就是不连续的函数;若循环的方式每个值持续10个时间步,那么这样做有什么益处呢?
RA价值的使用方法
RA价值提供了一个以敏捷策略为条件的价值预测,若价值函数$\hat{V}(o^{RA})\ge V_{threshold}=-0.05$,那么策略就会切换到恢复策略,从而使智能体基于合适的位姿势避障。
为了避障,其位姿命令应为
$$
\begin{aligned}
tw^{c}=[v_x^c,v_y^c,0,0,w_z^c]
\end{aligned}\tag{13}
$$
基于如下优化问题获得位姿命令
$$
\begin{aligned}
tw^{c}=argmin\quad d_{goal}^{future} \\
s.t.\hat{V}([tw^c;G^c_{x,y};R])\lt V_{threshold}
\end{aligned}\tag{14}
$$
注:这一部分也给出了一个线性积分以获得求解优化问题,不过没看明白啥意思?
恢复策略的学习
恢复策略的任务是追踪位姿命令,因此其观测空间与敏捷策略有所不同。
观测空间$o^{Rec}$由脚接触点$c_f$、基座角速度$w$、以及基座投影重力$g$,还有上一时间步基座的位姿命令$tw^c$、关节位置$q$、关节速度$\dot{q}$、以及动作$a$。
奖励函数
与敏捷策略一致,奖励函数由任务奖励、惩罚奖励、以及正则化奖励构成。除了允许knee与地面接触外,惩罚奖励和正则化奖励与敏捷策略中一致。
任务奖励为
$$
\begin{aligned}
r_{task}=10\cdot r_{linvel}-0.5\cdot r_{angvel}+5\cdot r_{alive}-0.1\cdot r_{posture}
\end{aligned}\tag{15}
$$
式(15)中$r_{linvel}$为追踪$v_x^c,v_y^c$项,$r_{angvel}$为追踪$w_z^c$,$r_{alive}$保持活跃,以及$r_{posture}$鼓励保持可随时切换策略姿势的奖励项。
确定来说,各项的定义为
$$
\begin{aligned}
r_{linvel} = exp[-\frac{(v_x-v_x^c)^2+(v_y-v_y^c)^2}{\sigma^2_{linvel}}]
\end{aligned}\tag{16}
$$
$$
\begin{aligned}
r_{angvel} = \Vert w_z-w_z^c\Vert^2_2
\end{aligned}\tag{17}
$$
$$
\begin{aligned}
r_{alive} = 1\cdot\mathbb{1}(alive)
\end{aligned}\tag{18}
$$
$$
\begin{aligned}
r_{posture} = \Vert q-\bar{q}_{rec}\Vert_1
\end{aligned}\tag{19}
$$
式(16)中$\sigma_{linvel}=0.5m/s$。
式(19)中$\bar{q}_{rec}$为低高度的标准站立姿势。
模型训练时,对课程和episode随机化进行了修改,其它与敏捷策略学习时一致。
感知
模型训练阶段,外部感知为$[-\frac{\pi}{4},\frac{\pi}{4}]$范围均匀分布的11维的射线距离。模型部署阶段,以深度图像预测的距离为感知,即需要学习一个射线预测网络。基于射线距离的方式能够降低成本,且降低算法学习复杂度的优点。
感知模型的数据集来源于仿真环境中深度图片与射线距离构成组合对的数据集。同时,为了能够适应真实环境也进行了数据增强。
相关思考
对于机器人的运动来说,最重要的不是使用的算法,而是其学习框架、背后的动机、奖励设计、以及Sim-to-Real的实现方式。
基于RL快速运动把机器人实现高速运动的问题转化为机器人如何在速度取值范围较大或系统参数取值范围较大内学习策略的问题,主要的创新点在于提出了自适应课程学习。与之相比,ABS通过追踪目标的方式,在敏捷奖励中加入最高速度项以使机器人能够学习到高速策略。
相较于追踪速度,基于位置追踪的方式使机器人更灵活。但是,位置追踪奖励设计有点费解,因为在最初收不到奖励,只有在最后$T_s$秒时才收到奖励。在询问作者之后,作者的回复是机器人由高速在$T_{s}$内停在目标位置,这是根据直觉设定的。那么,可以这样理解整体设计,机器人遇到障碍物停下来切换到恢复策略,绕过障碍物之后再以敏捷策略运行。
引用方法
请参考:
li,wanye. "ABS:学习无碰撞高速运动". wyli'Blog (Feb 2024). https://www.robotech.ink/index.php/archives/211.html
或BibTex方式引用:
@online{eaiStar-210,
title={ABS:学习无碰撞高速运动},
author={li,wanye},
year={2024},
month={Feb},
url="https://www.robotech.ink/index.php/archives/211.html"
}