Diffuser：敏捷行为合成的扩散规划器

基于模型的RL算法往往需要先估计一个环境模型，然后再基于该模型进行轨迹优化。然而，现实任务估计出准确的环境模型很难，且可能不适合轨迹优化。若把规划或轨迹优化等同于采样问题，即直接生成轨迹，那么可规避掉模型不准确的问题。Diffuser是一个基于扩散的规划方法，可见图1所示。

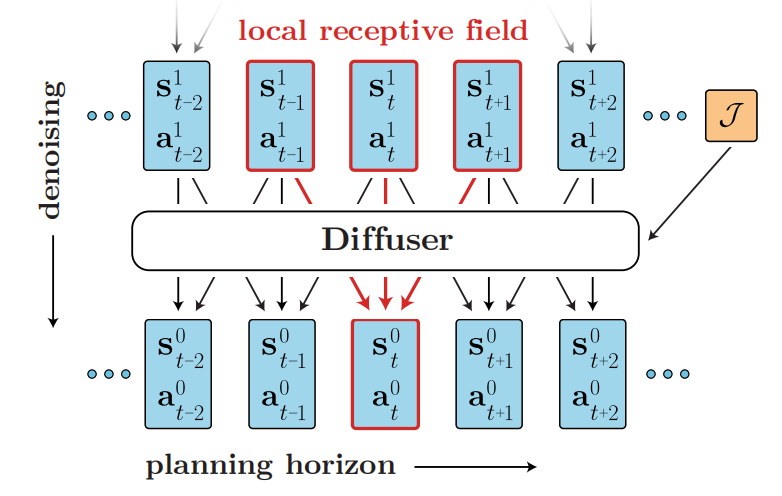
图1 Diffuser采样规划

问题设置

考虑一个离散时间动力学控制的系统$s_{t+1}=f(s_t,a_t)$，轨迹优化是指寻找一个动作序列$a_{0:T}^*$，可最大化目标函数
$$
\begin{aligned}
a^{*}_{0:T}=\underset{a_{0:T}}{argmax}\mathcal{J}(s_0,a_{0:T})=\underset{a_{0:T}}{argmax}\sum_{t=0}^T r(s_t,a_t)
\end{aligned}\tag{1}
$$
式(1)中$T$为规划的窗口。

基于扩散的规划

扩散规划器把尽可能多的规划过程纳入到生成建模框架中，从而使规划等同于采样。确切的说，基于轨迹的扩散模型$p_{\theta}(T)$，其去噪过程为
$$
\begin{aligned}
\tilde{p}_{\theta}(\tau)\propto p_{\theta}(\tau)h(\tau)
\end{aligned}\tag{2}
$$
式(2)中扰动函数$h(\tau)$可为先验信息、期望目标、奖励函数或成本函数。从而，去噪过程可视为轨迹优化问题，这是因为需要找到满足物理真实性$p_{\theta}(\tau)$和高奖励$h(\tau)$的轨迹。

轨迹规划的生成模型

这种把轨迹生成采样与规划视作相同问题的方式，产生了一个约束：无法按照时序的方式自回归的预测状态。虽然无法自回归的方式建模，但是可基于轨迹的局部连续性进行预测，即预测的感受野由过去和未来的时间步构成，可见图1所示。Diffuser是一个规划轨迹的模型，因此需要联合预测状态和轨迹。为此，作者们确立了模型架构形成的原则：

• 整个轨迹应非自回归的预测。
• 去噪过程的每步应具有时序局部性。
• 轨迹表示应沿着规划窗口的维度具有方差不变性。

基于以上原则，作者们设计了一个由重复的时序卷积残差块构成的模型，其架构类似于U-Nets，可见图2所示。由于模型属于全卷积的，所以预测的窗口不是由模型架构决定的，而是输入维度决定的。

图2 Diffuser架构

模型训练：Diffuser参数化一个轨迹去噪过程可学习的梯度$\epsilon_{\theta}(\tau^{i},i)$，目标函数为
$$
\begin{aligned}
\mathcal{L}(\theta)=\mathbb{E}_{i,\epsilon,\tau^0}[\Vert\epsilon-\epsilon(\tau^i,i)\Vert^2]
\end{aligned}\tag{3}
$$

Guided Sampling

为了利用Diffuser解决RL问题，作者们引入了奖励的概念。若$\mathcal{O}_t$为表示轨迹的第$t$个时间步的最优性的二值随机变量，且$p(\mathcal{O}_t=1)=exp(r(s_t,a_t))$，那么通过设置式(1)中$h(\tau)=p(\mathcal{O}_{1:T}\vert\tau)$进行采样
$$
\begin{aligned}
\tilde{p}_{\theta}(\tau)=p(\tau\vert\mathcal{O}_{1:T}=1)\propto p(\tau)p(\mathcal{O}_{1:T}=1\vert\tau)
\end{aligned}\tag{4}
$$
可以理解为把RL问题视作条件采样问题。根据基于扩散模型的条件采样相关工作，可知，若$p(\mathcal{O}_{1:T}\vert\tau^i)$足够平滑，那么逆扩散过程转换可被近似为高斯过程：
$$
\begin{aligned}
p_{\theta}(\tau^{i-1}\vert\tau^i,\mathcal{O}_{1:T})\approx\mathcal{N}(\tau^{i-1};\mu+\Sigma g,\Sigma)
\end{aligned}\tag{5}
$$
式(5)中$\mu,\Sigma$为原始逆转换过程$p_{\theta}(\tau^{i-1}\vert\tau^{i})$的参数且
$$
\begin{aligned}
g &= \nabla_{\tau}logp(\mathcal{O}_{1:t}\vert\tau)\vert_{\tau=\mu}\\
&=\sum_{t=0}^T\nabla_{s_t,a_t}r(s_t,a_T)\vert_{(s_t,a_t)=\mu_t}=\nabla\mathcal{J}(\mu)
\end{aligned}\tag{6}
$$
由此，分类器引导的采样与RL问题之间产生了一个直接的联系。首先，基于离线数据集训练一个扩散模型$p_{\theta}(\tau)$。接下来，再训练一个独立模型$\mathcal{J}_{\phi}$预测轨迹样本$\tau^i$的累积奖励。累积奖励模型$\mathcal{J}_{\phi}$的梯度用于引导采样，生成轨迹。最终，轨迹的第一个动作用于执行，具体的伪代码可见算法1所示。

图2 Guided扩散规划

其中，只执行轨迹中第一个动作的方式被称为回退窗口控制，这与扩散策略有异曲同工之妙。对于奖励函数$\mathcal{J}{\phi}$，网络架构由扩散模型U-Net的前一半，与一个输出层为线性层相组合构成。

Impainting

若规划问题为满足约束的问题，那么目标函数应该是生成任何满足约束的可行轨迹，例如：到达目标位置。在这种场景下，满足约束问题可被转换为inpainting问题。其中，状态或动作约束类比于图片中被观测到的像素，而无明确约束的位置类比于未观测到的像素。那么，该任务的扰动函数对于观测值为Dirac delta，而其它值为0，可见式(7)
$$
\begin{aligned}
h(\tau)=\delta_{c_t}(s_0,a_0,\ldots,s_t,a_t)=\begin{cases}
+\infty & if\quad c_t=s_t \\
0 & otherwise
\end{cases}
\end{aligned}\tag{7}
$$
对于动作的约束，也是相同的定义。在实践中，从未扰动逆扩散过程$\tau^{i-1}\sim p_{\theta}(\tau^{i-1}\vert\tau^i)$中采样。同时，在所有扩散步骤之后，基于条件值$c_t$替换掉采样值。

这里的替换笔者不是特别理解，需要阅读inpainting论文进一步理解。

扩散规划器的特性

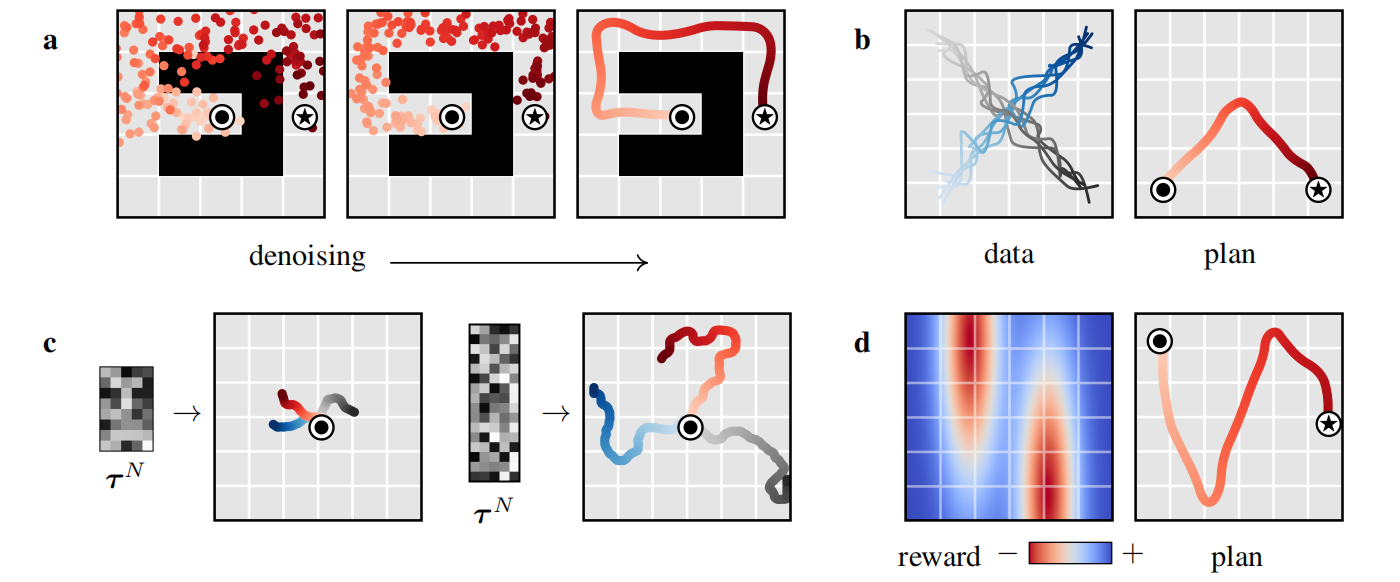
图3 扩散规划器特性

可学习长期规划：由于扩散规划等同于采样，所以Diffuser有效的作为长程预测器，执行长程规划，可见图3.a所示。

时序组合性：单步模型受到MDP的影响，从而组合分布中的转换以泛化分布之外的轨迹。Diffuser通过迭代提升局部连续性产生全局一致轨迹，因此可基于新颖的方式把相似子序列组合在一起，可见图3.b所示，模型生成了V型轨迹。

可变长度规划：可见图3.c所示，规划长度不取决于模型架构，而是输入的序列长度。

任务组合性：虽然Diffuser包含环境动力学和行为的信息，但是它与奖励函数之间相互独立。因此，可基于不同的奖励函数进行规划。如图3.d所示，基于新奖励函数规划的效果。

相关思考

扩散规划器与扩散策略有很多相似之处。与之不同，扩散规划器是基于轨迹优化的视角，而扩散策略是基于模仿学习的视角。同时，扩散规划器不是一个自回归模型，而是直接预测一个窗口内的状态-动作组合对。Diffuser把解决RL问题视作条件采样问题，把满足约束的规划问题视作inpainting问题，从而获得最优轨迹。