FoundationPose:统一新对象的6D位姿估计与追踪
对于机器人操作任务,对象位姿估计非常的重要。经典的实例级别的方法只能适用于特定的实例,这种方法通常需要CAD模型才能对新对象进行位姿估计。同时,类别级别的方法只能适用于特定类别,且训练数据的构造非常困难。为了处理这些限制,对任意对象的实时位姿估计受到到关注,主要有两种方法分别是有模型与无模型。其中,无模型的方法需要对象的参考图片。同时,位姿追踪利用时序线索实现高效、平滑的位姿估计。位姿追踪与位姿估计面临相同的限制。由此,FoundationPose做出了如下创新:
- 对新对象的位姿估计与追踪,设计了一个统一的框架,且支持有模型与无模型场景。为了应对有无模型之间的差别,设计了对象为中心的神经隐式表示用于高效的新视角合成。
- 提出了一个LLM辅助的合成数据生成的流程,该方法可被扩展到各种各样3D训练数据。
- 基于Transformer网络架构的新颖设计与对比学习方式使模型只需要在合成数据上训练,就可以实现较强的泛化性。
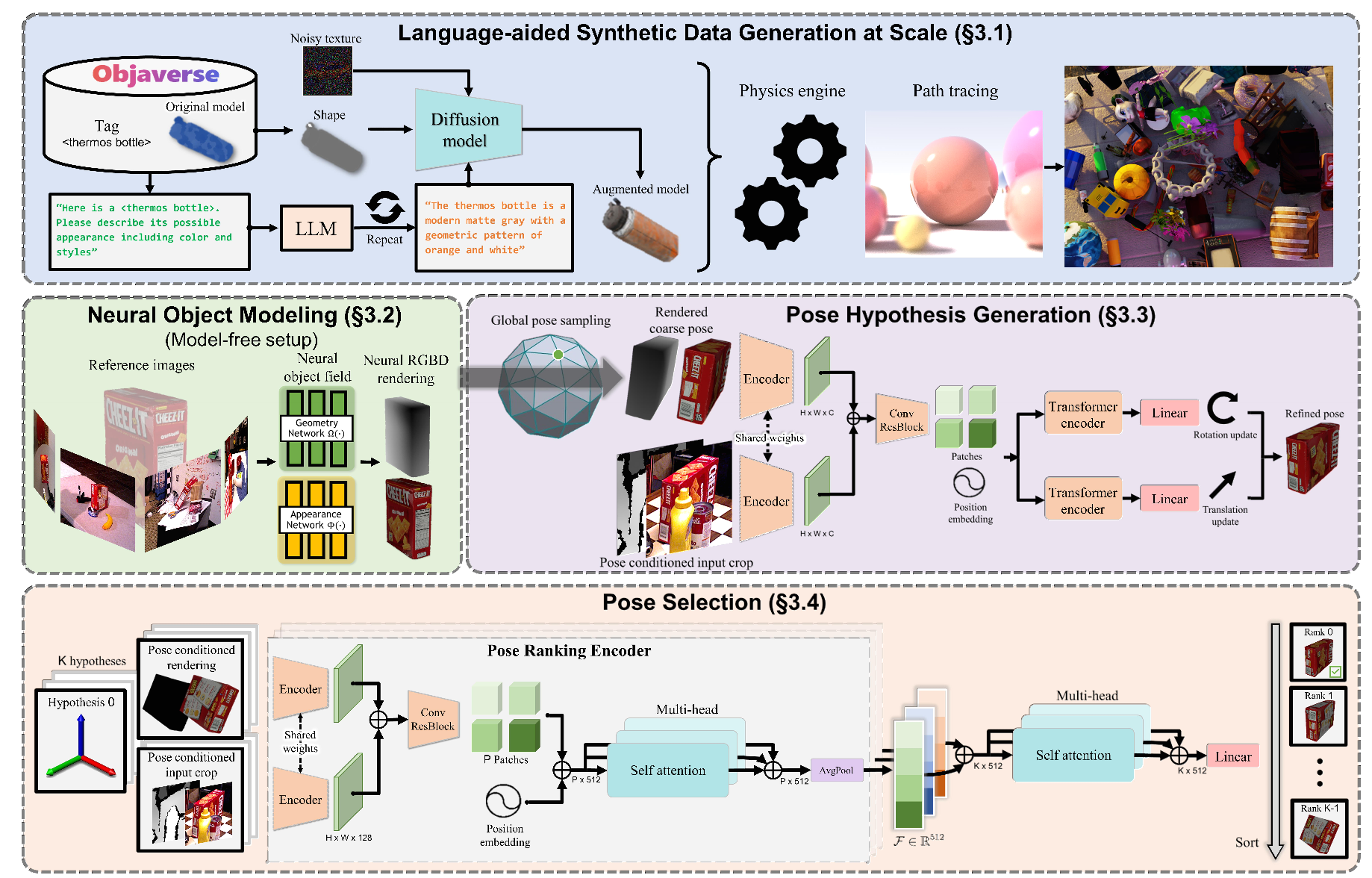
图1 FoundationPose架构
语言辅助的大规模数据生成
为了实现较强的泛化性,各种各样的对象与场景被需要。在真实世界,由于6D位姿估计,获得这种数据成本是很高的。作者们基于3D模型数据库、大语言模型、以及扩散模型设计了一个新颖的数据合成流程。利用的3D数据库主要有Objaverse与GSO。对于Objaveerse,选择了Objaveerse-LVIS子集数据。
大语言模型辅助的纹理增强
如图1-top所示,以文本提示、对象形状、以及随机初始化的噪音纹理为TexFusion输入,然后输出增强的纹理模型。对于文本提示,作者们提示ChatGPT模型,使其描述对象可能的外表,且ChatGPT的提示被模版化,从而大规模的生成文本提示。确切的说,作者们在NVIDIA Issac Sim环境中实现数据合成。
神经对象建模
对于无模型场景,无法获取3D的CAD模型。因此,作者们利用神经隐式表示用于对象建模。
Field Representation:如图1-middle-left所示,作者们利用两个函数表示对象。对于几何函数$\Omega:x\to s$,以3D点$x\in\mathbb{R}^3$为输入,输出一个有符号的距离值$s\in\mathbb{R}$;对于外表函数$\Phi:(f_{\Omega(x)},n,d)\to c$,以几何网络输出的特征向量$f_{\Omega(x)}$、点坐标$n\in\mathbb{R}^3$、以及视角方向$d\in\mathbb{R}^3$为输入,输出颜色$c\in\mathbb{R}_{+}^3$。其中,$x$输入神经网络之前进行了多分辨率哈希编码,$n$与$d$被嵌入到二阶球面谐波系数的固定集合。隐式对象的表面通过采用有符号域SDF:$S=\{x\in\mathbb{R}^3\vert\Omega(x)=3\}$的零值子集获得。与NeRF相比,SDF表示$\Omega$提供了高质量的深度渲染,且移除了选择密度阈值的需要。
Field Learning:对于纹理学习,作者们按照裁剪近表面区域的体积渲染方法:
$$
\begin{aligned}
c(r)=\int_{z(r)-\lambda}^{z(r)+0.5\lambda}w(x_i)\Phi(f_{\Omega(x_i)},n(x_i),d(x_i))dt
\end{aligned}\tag{1}
$$
$$
\begin{aligned}
w(x_i)=\frac{1}{1+e^{-\alpha\Omega(x_i)}}\frac{1}{1+e^{\alpha\Omega(x_i)}}
\end{aligned}\tag{2}
$$
式(1)中$z(r)$为深度图像的射线深度值,$\lambda$为裁剪距离。根据式(1),可知,忽视了距离表面超过$\lambda$的空空间,积分到$0.5\lambda$的穿透距离。在模型训练阶段,以颜色为监督,其目标函数为
$$
\begin{aligned}
\mathcal{L}_c=\frac{1}{\vert\mathcal{R}\vert}\sum_{r\in\mathcal{R}}\Vert c(r)-\bar{c}(r)\Vert_2
\end{aligned}\tag{3}
$$
式(3)中$\bar{c}(r)$为射线$r$行进方向的真实颜色。
对于几何学习,利用混合SDF模型,形成了空空间损失和近表面损失。同时,还对近表面SDF利用了eikonal正则化:
$$
\begin{aligned}
\mathcal{L}_e=\frac{1}{\vert\mathcal{X}_e\vert}\sum_{x\in\mathcal{X}_e}\vert\Omega(x)-\lambda\vert
\end{aligned}\tag{4}
$$
$$
\begin{aligned}
\mathcal{L}_s=\frac{1}{\vert\mathcal{X}_s\vert}\sum_{x\in\mathcal{X}_s}\vert\Omega(x)+d_x-d_D\vert
\end{aligned}\tag{5}
$$
$$
\begin{aligned}
\mathcal{L}_{eik}=\frac{1}{\vert\mathcal{X}_s\vert}\sum_{x\in\mathcal{X}_s}(\Vert\nabla\Omega(x)\Vert_2-1)
\end{aligned}\tag{6}
$$
式(4)-(6)中$x$为划分空间中沿着射线方向的3D点;$d_x$与$d_D$分别为射线原点到采样点的距离和观测深度。最终,损失函数为
$$
\begin{aligned}
\mathcal{L}=w_c\mathcal{L}_c+w_e\mathcal{L}_e+w_s\mathcal{L}_s+w_{eik}\mathcal{L}_{eik}
\end{aligned}\tag{7}
$$
对于新对象,只需要训练一次,且训练速度在秒级别。
Rendering:一旦训练完成,神经隐式表示被用于高效渲染对象。在这一过程,不仅仅渲染了颜色,且渲染了深度。在模型推理阶段,对于给定对象的位姿,按照栅格化过程渲染RGBD图片。
位姿假设生成
位姿初始化:对于给定RGBD图片,利用Mask R-CNN或CNOS检测对象。利用检测到的2D有界box内位于中心深度的3D点作为初始平移。为了初始化旋转,均匀从相机朝向的方向的一个以对象为中心的icosphere采样$N_s$个视角。同时,相机的位姿被$N_i$个平面内离散化旋转增强,由此共得到$N_s\cdot N_i$个初始化位姿。
位姿精炼:由于之前步骤的粗糙位姿初始化相当有噪音,因此需要精炼的模块提升位姿质量。确切的说,作者们训练了一个位姿精炼网络,该网络以粗糙位姿为条件的对象渲染与来自相机的被裁剪的输入观测为输入,输出更新后的位姿。与MegaPose为了寻找锚点对粗糙位姿进行了多视角渲染不同,作者们只对一个粗糙位姿渲染单个视角。对于输入观测,利用了位姿为条件的裁剪策略得到,而不是目标检测的边界框裁剪得到,从而为平移更新提供反馈。确切的说,作者们先把对象原点投射到图片空间,从而确定裁剪中心。接下来,再把对象表面两点之间距离最大的连线投射到图片空间,从而确定裁剪的大小以包裹对象及其附近背景。这种裁剪是以粗燥的位姿为条件,从而使网络更新变换,使裁剪更好的与观测对齐。这种精炼过程可被重复多次,从而提升位姿质量。
如图1-middle-right所示,精炼网络架构。首先从两个RGBD输入分支中抽取特征地图,这两个分支共享一个编码器。接下来,特征地图被concat,再输入到CNN模块。最后,输入到Transformer预测相对相机位姿的平移更新$\Delta\mathbf{t}\in\mathbb{R}^3$和相对相机位姿的旋转更新$\Delta\mathbf{R}\in\mathbb{SO}(3)$。那么,
$$
\begin{aligned}
\mathbf{t}^{+}=\mathbf{t}+\Delta\mathbf{t}
\end{aligned}\tag{8}
$$
$$
\begin{aligned}
\mathbf{R}^{+}=\Delta\mathbf{R}\otimes\mathbf{R}
\end{aligned}\tag{9}
$$
其目标函数为
$$
\begin{aligned}
\mathcal{L}_{refine}=w_1\Vert\Delta\mathbf{t}-\Delta\mathbf{\bar{t}}\Vert_2+w_2\Vert\Delta\mathbf{R}-\nabla\bar{\mathbf{R}}\Vert_2
\end{aligned}\tag{10}
$$
位姿选择
对于给定的精炼位姿假设,利用层级位姿排序网络计算其分数,选择分数最高的作为最终估计。
层级比较:首先,对每个假设,利用图1-bottom-left网络架构对比渲染的图片与位姿为条件被裁剪的输入观测,从而得到特征向量$\mathcal{F}\in\mathbb{R}^{512}$,用于描绘渲染与观测的对其质量。为了考虑所有位姿假设,把所有位姿假设的特征向量$\mathbf{F}=[\mathcal{F}_0,\ldots,\mathcal{F}_{K-1}]^T\in\mathbb{R}^{K\times512}$输入图1-bottom-right的网络架构,预测每个位姿假设的分数$\mathbf{S}\in\mathbb{R}^K$。
对比验证:为了训练位姿排序网络,作者们提出了一个位姿为条件三元损失
$$
\begin{aligned}
\mathcal{L}(i^+,i^-)=max(\mathbf{S}(i^-)-\mathbf{S}^{+}+\alpha,0)
\end{aligned}\tag{11}
$$
式(11)中$\alpha$为对比幅度;$i^+$与$i^-$分别为位姿正样本与负样本。
其中,正负样本由ADD度量确定。与标准的三元损失不同,锚样本不共享。虽然可以计算列表中每对损失,但是若两个位姿都距离真实标记较远会导致比较变得非常模糊。因此,作者们只考虑来自足够接近真实样本的一个视角下的正样本:
$$
\begin{aligned}
\mathbb{V}^{+}=\{i:D(\mathbf{R}_i,\bar{\mathbf{R}})\lt d\}
\end{aligned}\tag{12}
$$
$$
\begin{aligned}
\mathbb{V}^{-}=\{0,1,2,\ldots,K-1\}
\end{aligned}\tag{13}
$$
$$
\begin{aligned}
\mathcal{L}_{rank}=\sum_{i^+,i^-}\mathcal{L}(i^+,i^-)
\end{aligned}\tag{14}
$$
式(12)-(14)中$\mathbf{R}_i$与$\bar{\mathbf{R}}$分别为假设旋转与真实旋转;$D(\cdot)$为两个旋转之间的geodesic距离。
引用方法
请参考:
li,wanye. "FoundationPose:统一新对象的6D位姿估计与追踪". wyli'Blog (Apr 2024). https://www.robotech.ink/index.php/archives/416.html
或BibTex方式引用:
@online{eaiStar-416,
title={FoundationPose:统一新对象的6D位姿估计与追踪},
author={li,wanye},
year={2024},
month={Apr},
url="https://www.robotech.ink/index.php/archives/416.html"
}