VQ-VAE：离散表示学习

与VAE相比，VQ-VAE的编码器输出是离散的编码。同时，利用向量量化(VQ)不仅可拥有方差小的特性，也可克服“后验坍塌”问题。其中，“后验坍塌”是指VAE的编码器若为性能优越的自回归解码器，那么隐式编码会被忽视。若隐式表示与可学习的自回归先验相结合，模型可生成高质量的样本，那么证明了学习到表示是高效用。

VQ-VAE的设计

对于VAEs，由编码网络、先验分布$p(z)$、以及一个解码器$p(x\vert z)$。其中，编码网络属于一个给定输入数据$x$下离散隐式随机变量$z$参数化的后验分布$q(z\vert x)$。

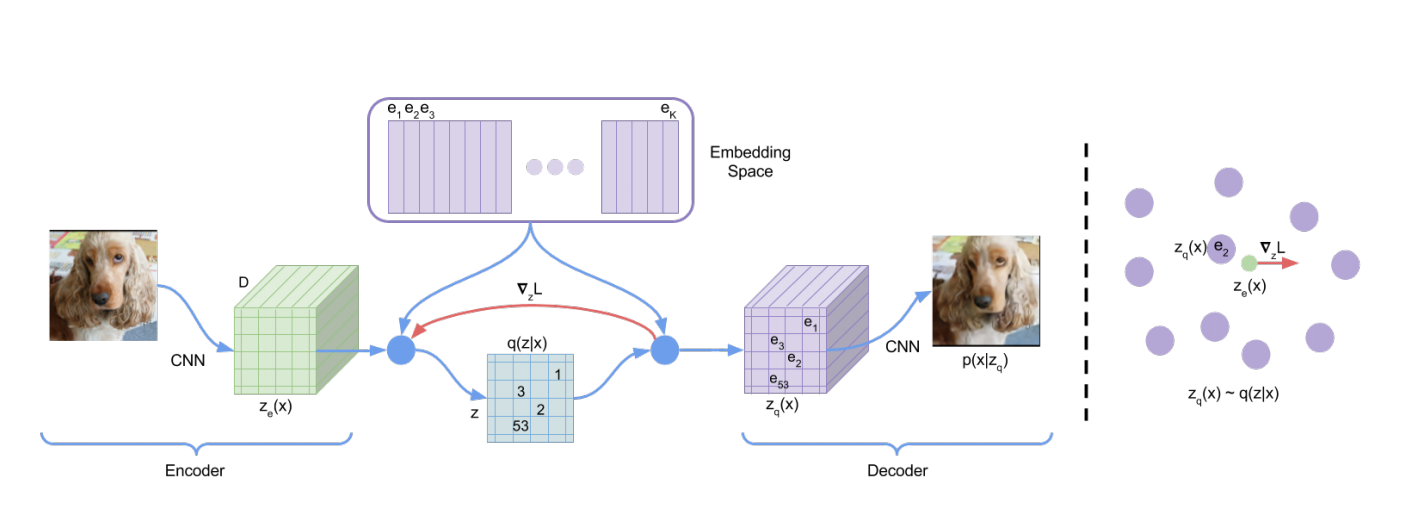
图1 VQ-VAE网络架构与Embedding空间可视化

离散隐式表示

定义一个隐式嵌入空间$e\in R^{K\times D}$，$K$为离散化隐式空间的大小，$D$为每个隐式嵌入向量$e_i$的维度，即共有$K$个embedding向量$e_i\in R^{D},i\in1,2,\ldots,K$。如图1(左)所示，模型以$x$为输入，编码器输出$z_e(x)$。离散化隐变量$z$通过共享embedding空间$e$的最近邻查找获得，可见式(1)所示。
$$
\begin{aligned}
q(z=k\vert x)=\begin{cases}1 & for~k=argmin_j\Vert z_{e}(x)-e_j\Vert_2,\\
0 & otherwise\end{cases}
\end{aligned}\tag{1}
$$
解码器的输入为对应的embedding向量$e_k$，可见式(2)所示。
$$
\begin{aligned}
z_q(x)=e_k,\quad where~k=argmin_j\Vert z_e(x)-e_j\Vert_2
\end{aligned}\tag{2}
$$
作者们认为分布$q(z=k\vert x)$为确定性的。若定义一个简单的均匀先验分布$z$，那么先验分布与后验分布之间的KL-Divergence为常数且等于$log K$。

学习

根据式(2)，可知，这里不存在真实的梯度。因此，作者们采用与straight-through估计器相似的方式，近似梯度。确切的说，只是简单的把解码器对输入的梯度复制到编码器输出。作者们也通过量化运算计算次梯度，但是这种估计器只在初始实验性能好。

在前向计算中，最近邻embedding $z_q(x)$被传递到解码器；在反向传递过程中，梯度$\nabla_z L$被无改变的传递到编码器。由于编码器的输出表示与解码器的输入共享相同$D$维空间，因此梯度包含了编码器如何改变输出而降低重构损失的有用信息。

如图1(右)所示，梯度可把编码器的输出在下一次前向传递过程中推动到不同离散化编码。

如式(3)所示，损失函数由三项构成，分别是重构损失项、向量量化目标函数、commitment损失。
$$
\begin{aligned}
L=logp(x\vert z_q(x))+\Vert sg[z_e(x)]-e\Vert_2^2+\beta\Vert z_e(x)-sg[e]\Vert_2^2
\end{aligned}\tag{3}
$$
式(3)中sg为停止梯度运算。

其中，向量量化损失以鼓励学习embedding空间，即该损失用于更新embedding字典，可替代的方式是利用$z_e(x)$的指数移动平均作为字典项；commitment损失为了确保编码器commit到一个embedding，其输出不会毫无限制的增长。

先验

离散隐式$p(z)$的先验分布是一个类别分布，可根据特征地图上其它$z$自回归得到。确切的说，在训练阶段，先验为常量且服从均匀分布。在训练之后，训练一个模型拟合$z$的自回归分布$p(z)$，从而可通过ancestral采样生成$x$。

相关思考

在模仿学习中，ACT算法在推理的时候就把后验设定为了常数，显然忽视了后验，这应该就是“后验坍塌”。