VAE：自动编码变分贝叶斯

VAE是要为带有连续隐变量的有向图模型推导出一个变分下界估计器，如图1所示。变分下界属于变分推断的内容，主要用于近似后验分布。

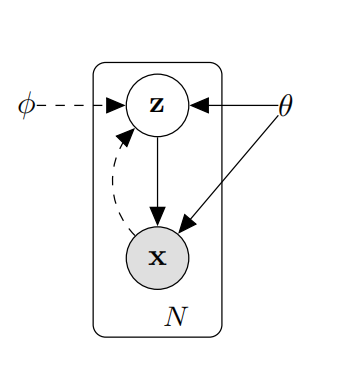
图1 有向图模型

若隐变量$\mathbf{z}$为连续性变量，那么贝叶斯公式的分母需要求积分，对于计算机来说积分是非常难求的，以往的变分推断技术是利用近似的方法，例如：mean-field 变分贝叶斯算法。然而，在深度神经网络的拟合能力下，可利用重参数化方式直接近似后验分布，这就产生了VAE。

问题定义

考虑$N$个独立同分布的连续型或离散型随机变量$\mathbf{x}$构成的数据集$\mathbf{X}=\{\mathbf{x}^{(i)}\}_{i=1}^N$。假设数据被包含随机变量$\mathbf{z}$的随机过程生成。该过程分为两步：

• 先验分布$p_{\theta^*}(\mathbf{z})$生成$\mathbf{z}^i$。
• 条件分布$p_{\theta^*}(\mathbf{x}\vert\mathbf{z})$生成${\mathbf{x}^i}$。

假设先验$p_{\theta^*}(\mathbf{z})$和似然$p_{\theta^*}(\mathbf{x}\vert\mathbf{z})$来自于分布$p_{\theta}(\mathbf{z})$和$p_{\theta}(\mathbf{x}\vert\mathbf{z})$的参数族，且概率密度函数处处可微。然而，真实的参数${\theta}^*$和隐变量$\mathbf{z}^i$不可知。在以上情况下，VAE作者们对三个问题感兴趣，分别是：

• 参数$\theta$的高效近似最大似然或最大后验估计方法。
• 基于观测$\mathbf{x}$下隐变量$\mathbf{z}$的高效近似后验推断方法。
• 随机变量$\mathbf{x}$的高效近似边缘分布推断方法。

变分界

边缘似然由每个数据点的似然和构成$logp_{\theta}(\mathbf{x}^{(1)},\cdots,\mathbf{x}^{(N)})=\sum_{i=1}^Nlogp_{\theta}(\mathbf{x}^i)$，且每一项可为
$$
\begin{aligned}
\mathcal{L}(\phi,\theta;\mathbf{x}^{i})&=\mathbb{E}_{z\sim q_{\phi(\cdot\vert x)}}log\frac{p_{\theta}(\mathbf{z},\mathbf{x}^i)}{q_{\phi}(\mathbf{z}\vert\mathbf{x}^i)}\\
&= \mathbb{E}_{z\sim q_{\phi}(\cdot\vert x)}logp_{\theta}(\mathbf{z},\mathbf{x}^i)-\mathbb{E}_{z\sim q_{\phi}(\cdot\vert x)}logq_{\phi}(\mathbf{z}\vert\mathbf{x}^i)\\
&=\mathbb{E}_{q_{\phi}(\mathbf{z}\vert\mathbf{x}^i)}[logp_{\theta}(\mathbf{x}^i\vert\mathbf{z})]-D_{KL}(q_{\phi}(\mathbf{z}\vert\mathbf{x}^i)\Vert p_{\theta}(\mathbf{z})) \\
&=\mathbb{E}_{q_{\phi}(\mathbf{z}\vert\mathbf{x}^i)}[logp_{\theta}(\mathbf{x}^i)]-D_{KL}(q_{\phi}(\mathbf{z}\vert\mathbf{x}^i)\Vert p_{\theta}(\mathbf{z}))
\end{aligned}\tag{1}
$$
其中，$q_{\phi}$为后验的近似。由于$D_{KL}$非负，所以
$$
\begin{aligned}
logp_{\theta}(\mathbf{x}^i)=\mathbb{E}_{q_{\phi}(\mathbf{z}\vert\mathbf{x}^i)}[logp_{\theta}(\mathbf{x}^i\vert\mathbf{z})]\ge\mathcal{L}(\theta,\phi;\mathbf{x}^{i})
\end{aligned}\tag{2}
$$
式(2)中$\mathcal{L}$是数据点$i$边缘似然的下界。只有近似后验分布与后验分布一致时，式(2)才取等号。因此，最大化下界就会使近似后验分布不断接近后验分布。然而，直接基于Monte Carlo估计下界的梯度会产生很大的方差，所以利用了重参数化技术。

SGVB估计器与AEVB算法

在特定温和的条件下，利用可微分的函数$g_{\phi}(\epsilon,\mathbf{x})$对随机变量$\tilde{\mathbf{z}}\sim q_{\phi}(\mathbf{z}\vert\mathbf{x})$进行重参数化，即
$$
\begin{aligned}
\tilde{\mathbf{z}}=g_{\phi}(\epsilon,\mathbf{x})\quad with\quad \epsilon\sim p(\epsilon)
\end{aligned}\tag{3}
$$
其中，$\epsilon$为随机噪音。那么，基于Monte Carlo估计函数$f(\mathbf{z})$的期望，见式(4)
$$
\begin{aligned}
\mathbb{E}_{q_{\phi}(\mathbf{z}\vert\mathbf{x}^{i})}[f(\mathbf{z})]=\mathbb{E}_{p(\epsilon)}[f(g_{\phi}(\epsilon,\mathbf{x}^{i}))]\simeq\frac{1}{L}\sum_{l=1}^Lf(g_{\phi}(\epsilon^{l},\mathbf{x}^{i}))\quad where \quad\epsilon^{(l)}\sim p(\epsilon)
\end{aligned}\tag{4}
$$
那么，把该技术应用于变分下界，产生随机梯度变分贝叶斯(SGVB)估计器$\tilde{\mathcal{L}}^A(\theta,\phi;\mathbf{x}^{(i)})\simeq\mathcal{L}(\theta,\phi;\mathbf{x}^{(i)})$
$$
\begin{aligned}
\tilde{\mathcal{L}}^{A}(\theta,\phi;\mathbf{x}^{(i)})=\frac{1}{L}\sum_{l=1}^L logp_{\theta}(\mathbf{z},\mathbf{x}^i)-logq_{\phi}(\mathbf{z}\vert\mathbf{x}^i)\\
where\quad\mathbf{z}^{(i,l)}=g_{\phi}(\epsilon^{(i,l)},\mathbf{x}^{(i)})\quad and\quad\epsilon^{(l)}\sim p(\epsilon)
\end{aligned}\tag{5}
$$
通常，$D_{KL}(q_{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})$通过解析的方式整合进式(5)。若$z$的先验为标准正态高斯分布，那么其后验也为高斯分布，且网络$\phi$只需要根据样本$x$预测高斯分布的均值和方差，从而生成$z$。因此，SGVB估计器可变为
$$
\begin{aligned}
\tilde{\mathcal{L}}^{B}(\theta,\phi;\mathbf{x}^{(i)})=\frac{1}{L}\sum_{i=1}^Llogp_{\theta}(\mathbf{x}^{(i)}\vert\mathbf{z}^{(i,l)})-D_{KL}(q_{\phi}(\mathbf{z}\vert\mathbf{x}^{(i)})\Vert p_{\theta}(\mathbf{z})) \\
where\quad\mathbf{z}^{(i,l)}=g_{\phi}(\epsilon^{(i,l)},\mathbf{x}^{(i)})\quad and\quad\epsilon^{(l)}\sim p(\epsilon)
\end{aligned}\tag{6}
$$

若基于minibatches的方式近似整个数据集的下界，实验发现，只要minibatches足够大，那么每个数据点的$L$可设置为1。由此，产生算法1。

算法1中式(8)为
$$
\begin{aligned}
\mathcal{L}(\theta,\phi;\mathbf{X})\simeq\tilde{\mathcal{L}}^{M}(\theta,\phi;\mathbf{X}^{M})=\frac{N}{M}\sum_{i=1}^{M}\tilde{\mathcal{L}}(\theta,\phi,;\mathbf{x}^{i})
\end{aligned}\tag{7}
$$
式(7)中$M$为数据量为$N$的数据集$X$中采样出数据点的数量。

由此自编码器算法形成，主要方法为：通过随机梯度上升的方式更新下界，从而使近似后验与后验分布之间的$KL$距离变小，重构误差变小。

重参数技巧

作者们还对重参数提出了一些方法：

• 可逆的累积分布函数。若$\epsilon\sim\mathcal{U}(0,\mathbf{I})$且$g_{\phi}(\epsilon,\mathbf{x})$为$q_{\phi}(\mathbf{z}\vert\mathbf{x})$逆的累积分布函数，例如：指数、柯西、帕累托分布等。
• 类比高斯样本，对于任何"location-scale"家族的分布，选择标准分布作为噪音分布，那么$g(\cdot)=location+scale\cdot\epsilon$，例如：拉普拉斯、均匀分布等。
• 构造：把随机变量表达为噪音变量的随机组合，例如：log-norm、gamma、以及beta分布等。

总的来说，$\epsilon$和$z$应该均为连续型随机变量。

相关思考

综上所述，对于估计带有连续型隐变量的观测变量，VAE先基于观测变量进行后验推断，从而近似后验分布。然后，再利用后验分布推断隐变量，从而利用隐变量生成观测数据。在现实世界中，直接对观测变量采样很难，VAE先对隐变量进行采样，然后再用隐变量得到观测变量。其中，隐变量一般为容易采样的分布，例如：高斯分布，这是通过设定得到。