机器人模仿动物的方式学习敏捷技能

基于强化学习范式的足式机器人能够在复杂的领域运动。然而，复杂的行为很难生成。同时，奖励设计和参数调节都需要花费很长的时间设计。

与强化学习相比，模仿学习不需要设计奖励函数，只需要基于参考运动获得期望技能。文献[1]基于模仿学习使机器人学习出敏捷的技能，并提出了模仿学习框架，可见图1所示。

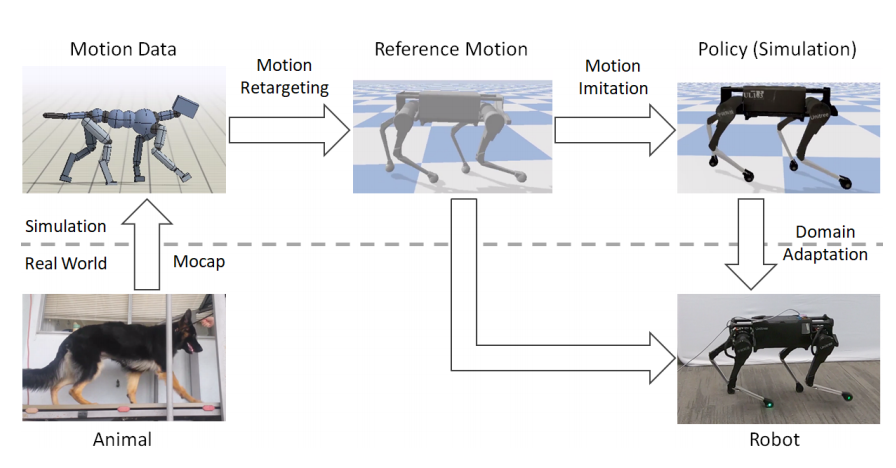
根据图1，可知，该模仿学习框架可分为运动再生成、运动模仿、以及领域自适应。运动在生成阶段，利用逆运动学把原始动物运动形态映射到机器人的形态；运动模仿阶段，在仿真环境中训练策略。同时，引入领域自适应训练模型。

运动再生成

动物的形态与机器人的形态往往是不同的，因此运动数据中动物形态需要与机器人形态对应。首先，把动物身体的关键点与机器人本体关键点对应。然后，确定运动数据中动物身体关键点的位置，再根据机器人姿势确定其关键点的位置。逆运动学被用于构建一系列姿势$\mathbf{q}_{0:T}$用于追踪关键点，对应的优化问题为
$$
\begin{aligned}
\underset{\mathbf{q}_{0:T}}{argmin}\sum_t\sum_i\Vert\hat{\mathbf{x}}_i(t)-\mathbf{x}_i(\mathbf{q}_t)\Vert^2+(\bar{\mathbf{q}}-\mathbf{q}_t)^T\mathbf{W}(\bar{\mathbf{q}}-\mathbf{q}_t)
\end{aligned}\tag{1}
$$
式(1)中正则化项是用于确定姿势与默认姿势$\bar{\mathbf{q}}$尽可能接近，$\mathbf{x}$表示关节位置。

运动模仿

与文献[2]中模仿运动方式类似，把模仿学习看成强化学习问题。策略网络的输入由状态$s_t$和目标$g_t$构成。其中，状态$s_t=(\mathbf{q}_{t-2:t},\mathbf{a}_{t-3:t-1})$表示过去3个时间步从IMU读取的本体姿势特征$\mathbf{q}_t$和动作$a_{t}$；目标$g_t=(\hat{\mathbf{q}}_{t+1},\hat{\mathbf{q}}_{t+2},\hat{\mathbf{q}}_{t+10},\hat{\mathbf{q}}_{t+20})$表示未来的目标姿势。与文献[2]类似，奖励函数为
$$
\begin{aligned}
r_t=w^p+r^p_t+w^vr^v_t+w^er^e_t+w^{rp}r^{rp}_t+w^{rv}+r^{rv}_t \\
w^p=0.5,\quad w^v=0.05,\quad w^e=0.2,\quad w^{rp}=0.15,\quad w^{rv}=0.1
\end{aligned}\tag{2}
$$
姿势奖励$r^p_t$鼓励机器人模仿参考运动：$r^p_t=exp[-5\sum_{j}\Vert\hat{\mathbf{q}}_t^j-\mathbf{q}_t^j\Vert^2]$

速度奖励：$r^v_t=exp[-0.1\sum_j\Vert\hat{\dot{\mathbf{q}}}_t^j-\dot{\mathbf{q}}_t^j\Vert^2]$

末端执行器奖励鼓励智能体追踪末端执行器的位置：$r^e_t=exp[-40\sum_e\Vert\hat{\mathbf{x}}_t^e-\mathbf{x}_t^e\Vert^2]$

本体姿势奖励和本体速度奖励均估计模仿本体运动，可见式(3)和(4)
$$
\begin{equation}
r_t^{rp}=exp[-20\Vert\hat{\mathbf{x}}_t^{root}-\mathbf{x}_t^{root}\Vert^2-10\Vert\hat{\mathbf{q}}_t^{root}-\mathbf{q}_t^{root}\Vert^2]\tag{3}
\end{equation}
$$

$$
\begin{equation}
r_t^{rv}=exp[-2\Vert\hat{\dot{\mathbf{x}}}_t^{root}-\dot{\mathbf{x}}_t^{root}\Vert^2-0.2\Vert\hat{\dot{\mathbf{q}}}_t^{root}-\dot{\mathbf{q}}_t^{root}\Vert^2]\tag{4}
\end{equation}
$$

领域自适应

领域自适应的目的是期望不仅学习到鲁棒性高的策略，策略也能随着环境的变化而变化。在每个episode开始，采样动力学参数$\mathbf{\mu}\sim\rho(\mathbf{\mu})$，再被编码器E编码为$\mathbf{z}\sim E(\mathbf{z}\vert\mathbf{\mu})$。策略模型以状态和环境编码为输入，输出动作，即$\pi(\mathbf{a}\vert\mathbf{s},\mathbf{z})$。在把策略迁移到真实世界时，与文献[3]相似，先寻找合适的编码$\mathbf{z}^*$使策略成功的执行期望动作。

为了解决策略对动力学参数$\mu$过拟合的问题，编码器中引入了信息瓶颈，目标函数为
$$
\begin{aligned}
\underset{\pi,E}{argmax}\quad\mathbb{E}_{\mu\sim\rho(\mu)}\mathbb{E}_{\mathbf{z}\sim E(\mathbf{z}\vert\mathbf{\mu})}\mathbb{E}_{\tau\sim p(\tau\vert\pi,\mu,\mathbf{z})}[\sum_{t=0}^{T-1}\gamma^t r_t]
\end{aligned}\tag{5}
$$

$$
\begin{aligned}
s.t.\quad I(\mathbf{M},\mathbf{Z})\le I_c
\end{aligned}\tag{6}
$$

计算互信息是不可行的，根据文献[4]，可知，式(6)可以利用编码$E$与变分先验$\rho(\mathbf{z})$之间的KL-Divergence被变分上界近似为
$$
\begin{aligned}
I(\mathbf{M},\mathbf{Z})\le\mathbb{E}_{\mu\sim\rho({\mu})}[D_{KL}[E(\cdot\vert\mu\Vert \rho(\cdot))]]
\end{aligned}\tag{7}
$$
那么，目标函数可以被进一步简化为拉格朗日函数
$$
\begin{aligned}
\underset{\pi,E}{argmax}\quad\mathbb{E}_{\mu\sim\rho(\mu)}\mathbb{E}_{\mathbf{z}\sim E(\mathbf{z}\vert\mathbf{\mu})}\mathbb{E}_{\tau\sim p(\tau\vert\pi,\mu,\mathbf{z})}[\sum_{t=0}^{T-1}\gamma^tr^t]-\beta\mathbb{E}_{\mu\sim\rho(\mu)}[D_{KL}[E(\cdot\vert\mu\Vert\rho(\cdot))]]
\end{aligned}\tag{8}
$$
式(8)中编码器被建模为高斯分布$E(\mathbf{z}\vert\mathbf{\mu})=\mathcal{N}(\mathbf{m}(\mu),\Sigma(\mu))$，先验$z$的分布$\rho(\mathbf{z})=\mathcal{N}(0,1)$。由此可见，目标函数可被解释为智能体策略最大化期望回报，同时也依赖最小的信息量适应环境的变化。

策略训练完成之后，通过AWR算法寻找到编码$\mathbf{z}^*$，其目标函数为
$$
\begin{aligned}
\mathbf{z}^*=\underset{\mathbf{z}}{argmax}\mathbb{E}_{\tau\sim p^*(\tau\vert\pi,\mathbf{z})}[\sum_{t=0}^{T-1}\gamma^tr_t]
\end{aligned}\tag{9}
$$
具体AWR算法可见图2所示

寻找到$\mathbf{z}^*$之后，就可以部署到真实世界了。

参考文献

[1] Peng X B, Coumans E, Zhang T, et al. Learning agile robotic locomotion skills by imitating animals[J]. arXiv preprint arXiv:2004.00784, 2020.

[2] Peng X B, Abbeel P, Levine S, et al. Deepmimic: Example-guided deep reinforcement learning of physics-based character skills[J]. ACM Transactions On Graphics (TOG), 2018, 37(4): 1-14.

[3] Yu W, Liu C K, Turk G. Policy transfer with strategy optimization[J]. arXiv preprint arXiv:1810.05751, 2018.

[4] Alemi A A, Fischer I, Dillon J V, et al. Deep variational information bottleneck[J]. arXiv preprint arXiv:1612.00410, 2016.