DFF：通过特征场蒸馏分解NeRF用于编辑

NeRF是一个有前景的场景表示方法，可根据观测图片实现高质量的3D重建和新视角合成。然而，编辑NeRF表示的场景有很大的挑战，尤其是选择性的编辑特定场景和对象。为了解决该问题，DFFs作者们把2D图片特征抽取器的知识蒸馏到3D特征场，且同时优化辐射场。最终，这种方式可使用户基于各种模态的查询，例如：文本、图片patch，把3D特征场语义的分解到3D空间，从而可语义上选择和编辑辐射场的特定区域。

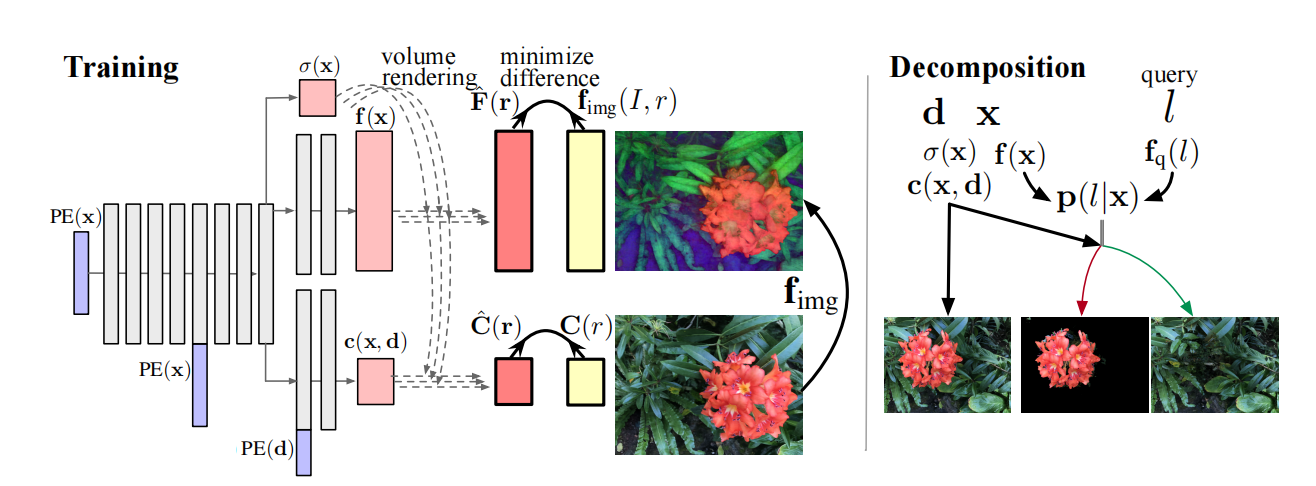
图1 DFF的训练与测试

通过体积渲染把基础模块蒸馏到3D特征场

NeRF通过神经网络预测3D场景中位置$\mathbf{x}$的密度$\sigma(\mathbf{x})$和视角依赖的颜色$\mathbf{c}(\mathbf{x},\mathbf{d})$。作者们通过增加解码器的方式扩展NeRF，用于预测感兴趣的量。确切的说，作者们增加一个特征分支以输出一个特征向量，用于描述每个3D空间点的语义。作者们利用像素级图片编码器$\mathbf{f}_{img}$作为teacher网络，用于对特征场进行监督训练。其中，图片编码器为LSeg中DPT网络架构。给定3D坐标点$\mathbf{x}$，特征场输出一个特征向量$f(\mathbf{x})$、密度$\sigma(\mathbf{x})$、以及颜色$\mathbf{c}(\mathbf{x},\mathbf{d})$，可见图1所示。与NeRF相似，利用体积渲染特征场：
$$
\begin{aligned}
\hat{\mathbf{F}}(\mathbf{r})=\sum_{k=1}^K\hat{T}(t_k)\alpha(\sigma(\mathbf{x}_k)\delta_k)\mathbf{f}(\mathbf{x}_k)
\end{aligned}\tag{1}
$$
通过最小化渲染特征$\hat{\mathbf{F}}(\mathbf{r})$与teacher特征$\mathbf{f}_{img}(I,r)$之间差距优化特征向量。这种方式是把2D teacher网络蒸馏到3D student网络，因此被称为特征场蒸馏(Distilled Feature Field,DFF)。与NeRF的目标函数相结合，形成
$$
\begin{aligned}
L=L_p+\lambda L_{f},L_{p}=\sum_{\mathbf{r}\in\mathcal{R}}\Vert\hat{C}(\mathbf{r})-\mathbf{C}(r)\Vert_2^2,L_{f}=\sum_{r\in\mathcal{R}}\Vert\hat{F}(\mathbf{r})-\mathbf{f}_{img}(I,r)\Vert_1
\end{aligned}\tag{2}
$$
式(2)中$\lambda=0.04$

由于teacher的特征$\mathbf{f}_{img}(I,r)$不是完全多视角一致的，因此在渲染特征$\hat{\mathbf{F}}(\mathbf{r})$时，对密度进行stop-gradient，否则会降低重建几何的质量。

基于Query的分解和编辑

一个训练好的DFF模型通过特征场$\mathbf{f}$和查询编码器$\mathbf{f}_q$执行零样本3D分割。在3D空间点$\mathbf{x}$中标签$l$的概率$\mathbf{p}(l\vert\mathbf{x})$，可通过3D特征$\mathbf{f}(\mathbf{x})$与文本标签特征$\mathbf{f}_{q}(l)$之间点积的softmax计算得到
$$
\begin{aligned}
\mathbf{p}(l\vert x)=\frac{exp(\mathbf{f}(\mathbf{x})\mathbf{f}_{q}(l)^T)}{\sum_{{l}'\in\mathcal{L}}(exp(\mathbf{f}(\mathbf{x})\mathbf{f}_{q}({l}')^T))}
\end{aligned}\tag{3}
$$
该方法即可形成基于查询的分割场。其中，标签编码器为LSeg中文本编码器，也即CLIP的文本编码器。

首先，对于单个场景的渲染为
$$
\begin{aligned}
\hat{\mathbf{C}}(\mathbf{r})=\sum_{k=1}^K\hat{T}(t_k)\alpha(\sigma(\mathbf{x}_k)\delta_k)\mathbf{c}(\mathbf{x}_k,\mathbf{d}),\quad\hat{T}(t_k)=exp(-\sum_{{k}'=1}^{k-1}\sigma(\mathbf{x}_{{k}'})\delta_{{k}'})
\end{aligned}\tag{4}
$$
基于DFF，各种编辑方法都可以融合两个NeRF，作者们利用分割场$\mathbf{p}$进行混合，可见
$$
\begin{aligned}
\hat{\mathbf{C}}(\mathbf{r})=\sum_{k=1}^K\hat{T}(t_k)(\alpha(\sigma_1(\mathbf{x}_k)\delta_k)\mathbf{c}_{1}(\mathbf{x}_k,\mathbf{d})p_k+\alpha(\sigma_{2}(\mathbf{x}_k)\delta_k)\mathbf{c}_2(\mathbf{x}_k,d)(1-\rho_k))
\end{aligned}\tag{5}
$$

$$
\begin{aligned}
where\quad\rho_k=\frac{\alpha(\sigma_1(\mathbf{x}_k)\delta_k)}{\alpha(\sigma_1(\mathbf{x}_k)\delta_k)+\alpha(\sigma_2(\mathbf{x}_k)\delta_k)},\hat{T}(t_k)=\prod_{{k}'=1}^{k-1}\alpha(\sigma_1(\mathbf{x}_{{k}'}\delta_{{k}'}))+\alpha(\sigma_2(\mathbf{x}_{{k}'}\delta_{{k}'})
\end{aligned}\tag{6}
$$

若对查询$l$的区域进行几何变形$g$，那么通过式(5)和式(6)渲染场景。其中，$\alpha(\sigma_1(\mathbf{x}_{k})\delta_k)=(1-\mathbf{p}(l\vert\mathbf{x}_k))\alpha(\sigma(\mathbf{x}_k)\delta_k)$,$\alpha(\sigma_2(\mathbf{x}_{k})\delta_k)=\mathbf{p}(l\vert\mathbf{g}^{-1}(\mathbf{x}_k))\alpha(\sigma(\mathbf{g}^{-1}(\mathbf{x}_k))\delta_k)$,$\mathbf{c}_1(\mathbf{x}_k,\mathbf{d})=(1-\mathbf{p}(l\vert\mathbf{x}_k))\mathbf{c}(\mathbf{x}_k,d)$以及$\mathbf{c}_2(\mathbf{x}_k,\mathbf{d})=\mathbf{p}(l\vert\mathbf{g}^{-1}(\mathbf{x}_k))\mathbf{c}(\mathbf{g}^{-1}(\mathbf{x}_k),\mathbf{g}^{-1}(\mathbf{d}))$

相关思考

SparseDFF作者们利用特征场蒸馏在dexterous manipulations任务上实现了one-shot学习的能力。确切的说，通过特征场蒸馏抽取3D对象的语义特征，从而允许操作能力在不同形状、位姿、以及外表的相同对象上迁移。